2021高考数学人教版一轮复习多维层次练:第二章 第7节 函数的图象
www.ks5u.com
多维层次练13
[A级 基础巩固]
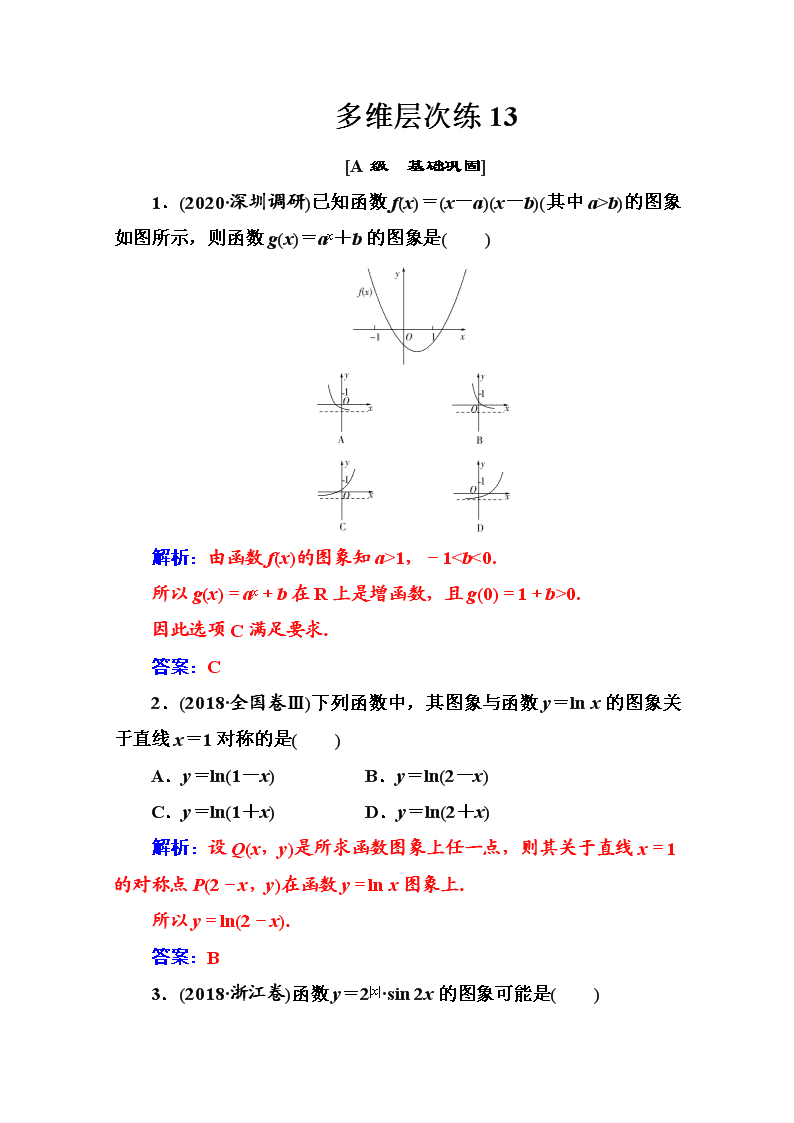
1.(2020·深圳调研)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )
解析:由函数f(x)的图象知a>1,-1
0.
因此选项C满足要求.
答案:C
2.(2018·全国卷Ⅲ)下列函数中,其图象与函数y=ln x的图象关于直线x=1对称的是( )
A.y=ln(1-x) B.y=ln(2-x)
C.y=ln(1+x) D.y=ln(2+x)
解析:设Q(x,y)是所求函数图象上任一点,则其关于直线x=1的对称点P(2-x,y)在函数y=ln x图象上.
所以y=ln(2-x).
答案:B
3.(2018·浙江卷)函数y=2|x|·sin 2x的图象可能是( )
解析:由y=2|x|sin 2x知函数的定义域为R,
令f(x)=2|x|sin 2x,则f(-x)=2|-x|sin(-2x)=-2|x|sin 2x.
因为f(x)=-f(-x),所以f(x)为奇函数.
所以f(x)的图象关于原点对称,故排除A,B.
令f(x)=2|x|sin 2x=0,解得x=(k∈Z),
所以当k=1时,x=,故排除C.故选D.
答案:D
4.若函数f(x)=的图象如图所示,则f(-3)等于( )
A.- B.-
C.-1 D.-2
解析:由图象知得
所以f(x)=故f(-3)=5-6=-1.
答案:C
5.(多选题)函数y=ax2+bx与函数y=xa+b(a≠0)在同一平面直角坐标系中的图象不可能为( )
解析:y=ax2+bx=a-,对于A,由二次函数图象可知,a<0,-<0,所以b<0,函数y=xa+b不符合要求,同理B不符合要求;对于C,D,由二次函数图象中知,a<0,->0,所以b>0,比较选项C,D,可知C符合要求.
答案:ABD
6.已知函数f(2x+1)是奇函数,则函数y=f(2x)的图象的中心对称的点为( )
A.(1,0) B.(-1,0)
C. D.
解析:f(2x+1)是奇函数,所以其图象关于原点成中心对称,而f(2x)的图象是由f(2x+1)的图象向右平移个单位得到的,故关于点成中心对称.
答案:C
7.(多选题)下列命题中正确的是( )
A.在同一坐标系中,y=log2 x与y=log x的图象关于x轴对称
B.函数y=的最小值是
C.函数y=的图象关于点(-2,1)对称
D.函数f(x)=2x-x2只有两个零点
解析:作y=log2x与y=logx的图象,易知A正确.
因为1-x2≤1,所以y=≥,知B正确.
又y==1-,
由于y=-关于(0,0)对称,
根据图象变换得y=的图象关于(-2,1)对称,C正确.
利用y=2x与y=x2图象交点,知f(x)=2x-x2有3个零点,D错.
答案:ABC
8.已知函数f(x)=|ln x|,若f(m)=f(n)(m>n>0),则+=( )
A. B.1
C.2 D.4
解析:函数f(x)=|ln x|的图象如图所示:
由f(m)=f(n),m>n>0,可知m>1>n>0,
所以ln m=-ln n,从而mn=1.
则+===2.
答案:C
9.若函数y=f(x)的图象过点(1,1),则函数y=f(4-x)的图象一定经过点________.
解析:由于函数y=f(4-x)的图象可以看作y=f(x)的图象先关于y轴对称,再向右平移4个单位长度得到.点(1,1)关于y轴对称的点为(-1,1),再将此点向右平移4个单位长度.
所以函数y=f(4-x)的图象过定点(3,1).
答案:(3,1)
10.若函数y=+m的图象与x轴有公共点,则实数m的取值范围是________.
解析:作出y=的图象(如图所示),欲使y=+m的图象与x轴有交点,则-1≤m<0.
答案:[-1,0)
11.(2020·济南质检)若直角坐标系内A、B两点满足:(1)点A、B都在f(x)图象上;(2)点A、B关于原点对称,则称点对(A,B)是函数f(x)
的一个“和谐点对”,(A,B)与(B,A)可看作一个“和谐点对”.已知函数f(x)=则f(x)的“和谐点对”有________个.
解析:作出函数y=x2+2x(x<0)的图象关于原点对称的图象(如图中的虚线部分),看它与函数y=(x≥0)的图象的交点个数即可,观察图象可得交点个数为2,即f(x)的“和谐点对”有2个.
答案:2
12.使log2(-x)0且x→0时,f(x)>0,
所以C项不满足,只有A项满足.
答案:A
2.利用函数的图象研究函数的性质
对于已知或易画出其在给定区间上图象的函数,其性质[单调性、奇偶性、周期性、最值(值域)、零点]的研究常借助于图象研究,但一定要注意性质与图象特征的对应关系.
[典例2] 已知max{a,b}表示a,b两数中的最大值.若f(x)=max{e|x|,e|x-2|},则f(x)的最小值为________.
解析:在同一直角坐标系中,画出函数y=e|x|,y=e|x-2|的图象(图略),
可知f(x)=max{e|x|,e|x-2|}=
当x≥1时,f(x)≥e,且当x=1时,取得最小值e;
当x<1时,f(x)>e.
故f(x)的最小值为f(1)=e.
答案:e
[典例3] (2020·西安质检)已知函数g(x)=-,h(x)=cos πx.当x∈(-2,4)时,函数g(x)与h(x)的交点横坐标分别记为xi(i=1,2,…,n),则i=( )
A.5 B.6 C.7 D.8
解析:易知g(x)=-的图象关于x=1对称,h(x)=cos πx的图象关于x=1对称.
作出两个函数的图象,如图所示.
根据图象知,两函数有7个交点,其中一个为x=1,另外6个交点关于直线x=1对称,
因此i=3×2+1=7.
答案:C
[解题思路] 解此类求图象交点横、纵坐标之和的问题,常利用图象的对称性求解,即找出两图象的公共对称轴或对称中心,从而得出各交点的公共对称轴或对称中心,由此得出定值求解.
3.利用图象求解函数零点或不等式
若研究的方程(不等式)不能用代数法求解,但其与基本初等函数有关,常将方程(不等式)问题转化为两函数图象的交点或图象的上下位置关系,然后借由图象的几何直观求解.
[典例4] (1)函数f(x)=2sin xsin-x2的零点个数为________.
(2)函数f(x)是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式<0的解集为________________.
解析:(1)f(x)=2sin xcos x-x2=sin 2x-x2,函数f(x)的零点个数可转化为函数y1=sin 2x与y2=x2
图象的交点个数,在同一坐标系中画出y1=sin 2x与y2=x2的图象如图所示:
由图可知两函数图象有2个交点,则f(x)的零点个数为2.
(2)当x∈时,y=cos x>0.
当x∈时,y=cos x<0.
结合y=f(x),x∈[0,4]上的图象知,
当1
查看更多