数学文卷·2017届湖南省郴州市高三第二次教学质量监测（2016

数学文卷·2017届湖南省郴州市高三第二次教学质量监测（2016

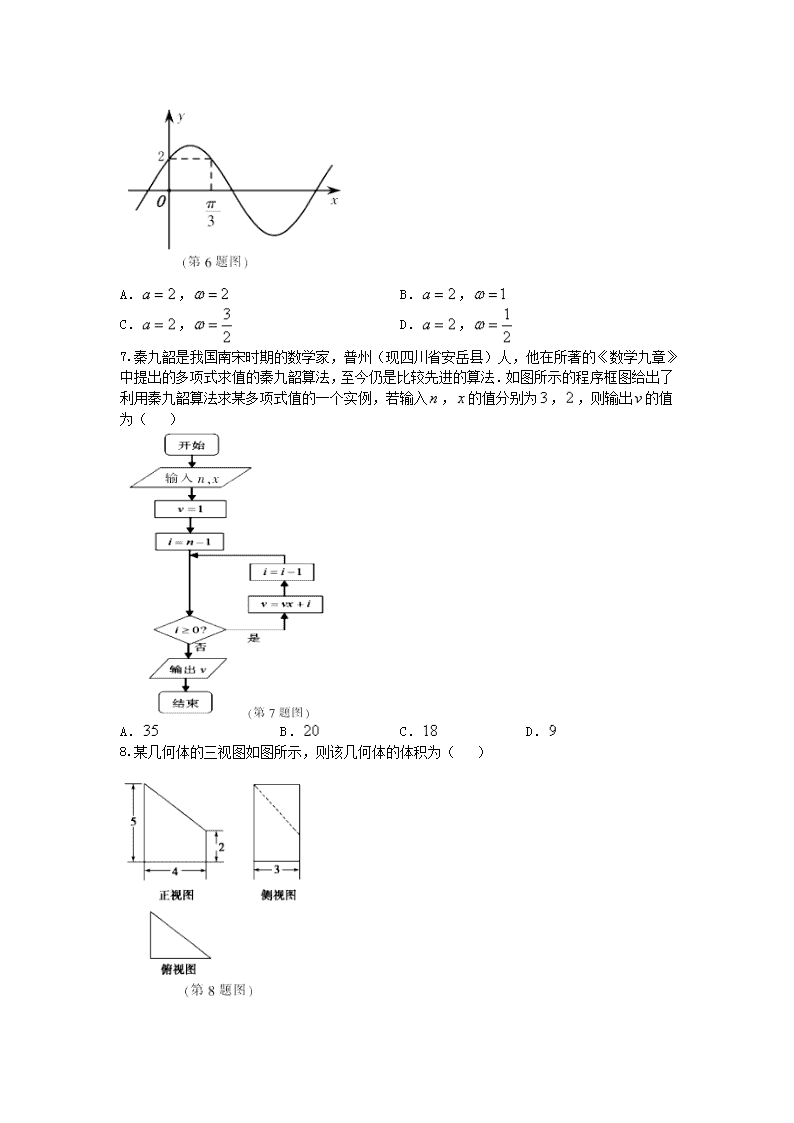
‎ ‎ 文科数学 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合，，则（ ）‎ A． B．‎ C． D．‎ ‎2.复数（为虚数单位）所对应的点位于复平面内（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3.从标有数字，，的三个红球和标有数字，的两个白球中任取两个球，则取得两球的数字和颜色都不相同的概率为（ ）‎ A． B． C． D．‎ ‎4.“”是“函数在区间上为增函数”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎5.已知双曲线的左右焦点分别为，，若双曲线左支上有一点到右焦点距离为，为的中点，为坐标原点，则等于（ ）‎ A． B． C． D．‎ ‎6.函数（，）的图象如图所示，则实数和的最小正值分别为（ ）‎ A．， B．，‎ C．， D．，‎ ‎7.秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数学九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入，的值分别为，，则输出的值为（ ）‎ A． B． C． D．‎ ‎8.某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎9.已知实数，满足不等式组，若目标函数的最大值不超过，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎10.函数的图象大致是（ ）‎ A． B．‎ C． D．‎ ‎11.已知等比数列的前项和，则等于（ ）‎ A． B． C． D．‎ ‎12.已知关于的方程有个不同的实数根，则实数的取值范围是（ ）‎ A． B． C． D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.已知，，与的夹角为，则____________．‎ ‎14.已知，，则____________．‎ ‎15.底面为正方形，顶点在底面的投影为底面中心的棱锥的五个顶点在同一球面上．若该棱锥的底面边长为，侧棱长为，则这个球的表面积为____________．‎ ‎16.已知抛物线：，点为抛物线上任意一点，过点向圆：作切线，切点分别为，，则四边形 面积的最小值为____________．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.（本小题满分10分）‎ 已知，，分别为的三个内角，，所对边的边长，且满足．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若，的面积为，求，．‎ ‎18.（本小题满分12分）‎ 在等差数列中，，．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列的通项公式为，求数列的前项的和．‎ ‎19.（本小题满分12分）‎ 年月，京津冀等地数城市指数“爆表”，北方此轮污染为年以来最严重的污染过程．为了探究车流量与的浓度是否相关，现采集到北方某城市年月份某星期星期一到星期日某一时间段车流量与的数据如表：‎ ‎（Ⅰ）由散点图知与具有线性相关关系，求关于的线性回归方程；‎ ‎（Ⅱ）（ⅰ）利用（Ⅰ）所求的回归方程，预测该市车流量为万辆时的浓度；‎ ‎（ⅱ）规定：当一天内的浓度平均值在内，空气质量等级为优；当一天内的浓度平均值在内，空气质量等级为良．为使该市某日空气质量为优或者为良，则应控制当天车流量在多少万辆以内？（结果以万辆为单位，保留整数．）‎ 参考公式：回归直线的方程是，其中，．‎ ‎20.（本小题满分12分）‎ 如图甲，在直角梯形中，，，，，是的中点，是与的交点，将沿折起到的位置，如图乙．‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）若平面平面，求点到平面的距离．‎ ‎21.（本小题满分12分）‎ 如图，已知圆：经过椭圆：（）的左右焦点，，与椭圆在第一象限的交点为，且，，三点共线．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设与直线（为原点）平行的直线交椭圆于，两点．当的面积取到最大值时，求直线的方程．‎ ‎22.（本小题满分12分）‎ 已知函数．‎ ‎（Ⅰ）求函数的最小值；‎ ‎（Ⅱ）设（），讨论函数的单调性；‎ ‎（Ⅲ）若斜率为的直线与曲线交于，两点，其中，求证：．‎ 郴州市2017届高三第二次教学质量监测试卷 数学（文科）参考答案及评分细则 一、选择题 ‎1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.‎ 二、填空题 ‎13. 14. 15. 16.‎ 三、解答题 ‎17.解：（Ⅰ），由正弦定理得：‎ ‎，………………………………………………………（2分）‎ ‎，…………………………………………………………………………………（5分）‎ ‎，‎ ‎………………………………………………………………………………………………（6分）‎ ‎（Ⅱ），所以，…………………………………………………………（7分）‎ ‎，，则（或 ‎），………………………………（8分）‎ 解得：．………………………………………………………………………………………（10分）‎ ‎18.解：（Ⅰ）设等差数列的公差为，由题意知：，，‎ 可得……………………………………………………………………………………（2分）‎ 解得……………………………………………………………………………………………（4分）‎ 所以．…………………………………………………………………………………………（5分）‎ ‎（Ⅱ）由（Ⅰ）可知，所以．…………………………………………………（6分）‎ ‎ ①…………………………………………………………（7分）‎ ‎ ②…………………………………………………………（8分）‎ ‎①②，得：‎ ‎………………………………………（9分）‎ 故：…………………………………………………………………………（10分）‎ 即．……………………………………………………………………………（12分）‎ ‎19.解：（Ⅰ）由数据可得：，…………………………………（1分）‎ ‎，……………………………………………………（2分）‎ ‎，，………………………………………………………………………（4分）‎ ‎，………………………………………………………………（6分）‎ ‎……………………………………………………………………………（7分）‎ 故关于的线性回归方程为．…………………………………………………………（8分）‎ ‎（Ⅱ）（ⅰ）当车流量为万辆时，即时，．‎ 故车流量为万辆时，的浓度为微克/立方米．………………………………………（10分）‎ ‎（ⅱ）根据题意信息得：，即，…………………………………………（11分）‎ 故要使该市某日空气质量为优或为良，则应控制当天车流量在万辆以内．…………………（12分）‎ ‎20.（本小题满分12分）‎ ‎（Ⅰ）证明：在图甲中，，，是的中点，，‎ ‎，…………………………………………………………………………………………（2分）‎ 即在图乙中，，．……………………………………………………………（3分）‎ 又，平面．…………………………………………………………（4分）‎ ‎，，‎ 四边形是平行四边形，‎ ‎，…………………………………………………………………………………………（5分）‎ 平面．…………………………………………………………………………………（6分）‎ ‎（Ⅱ）解：由已知，，平面平面，，‎ 平面，，……………………………………………………………（7分）‎ ‎，又由（Ⅰ）知，平面，平面，‎ ‎．‎ ‎，．………………………………………………………………………（9分）‎ 设到平面的距离为，且，，，‎ 由得：，…………………………（11分）‎ ‎，故到平面的距离为．………………………………………………………（12分）‎ ‎21.解：（Ⅰ），，三点共线，为圆的直径，且，‎ ‎．‎ 由，‎ 得，‎ ‎………………………………………………………………………………………………（2分）‎ ‎，‎ ‎，．…………………………………………………………………（3分）‎ ‎，，…………………………………………………………………………（4分）‎ 椭圆的方程为．……………………………………………………………………（5分）‎ ‎（Ⅱ）由（Ⅰ）知，点的坐标为，‎ 直线的斜率为………………………………………………………………………………（6分）‎ 故设直线的方程为，‎ 联立得，…………………………………………………（7分）‎ 设，，‎ ‎，，‎ ‎，‎ ‎．…………………………………………………………（8分）‎ 又 ‎…………………………………………………………（9分）‎ 点到直线的距离…………………………………………………………………（10分）‎ ‎，‎ 当且仅当，即时等号成立，‎ 此时直线的方程为．………………………………………………………………（12分）‎ ‎22.解：（Ⅰ）（），…………………………………………………………（1分）‎ 令，得，‎ 当时，；当时，．‎ 则在内递减，在内递增，…………………………………………………（2分）‎ 所以当时，函数取得最小值，且……（3分）‎ ‎（Ⅱ），（），………………………（4分）‎ 当时，恒有，在区间 内是增函数；………………………………（5分）‎ 当时，令，即，解得，‎ 令，即，解得，………………………………………………（6分）‎ 综上，当时，在区间内是增函数，当时，在内单调递增，在内单调递减．…………………………………………………………………………（7分）‎ ‎（Ⅲ）证明：，要证明，‎ 即证，…………………………………………………………………………（8分）‎ 等价于，令（由，知），‎ 则只需证，由，知，故等价于（）（）……（9分）‎ ‎①设（），则（），所以在内是增函数，当时，，所以；…………………………………………………（10分）‎ ‎②设（），则（），所以在内是增函数，所以当时，，即（）．………………………………（11分）‎ 由①②知（）成立，所以．…………………………………………………………（12分）‎