【数学】2020届一轮复习浙江专版7-6立体几何中的向量方法学案

【数学】2020届一轮复习浙江专版7-6立体几何中的向量方法学案

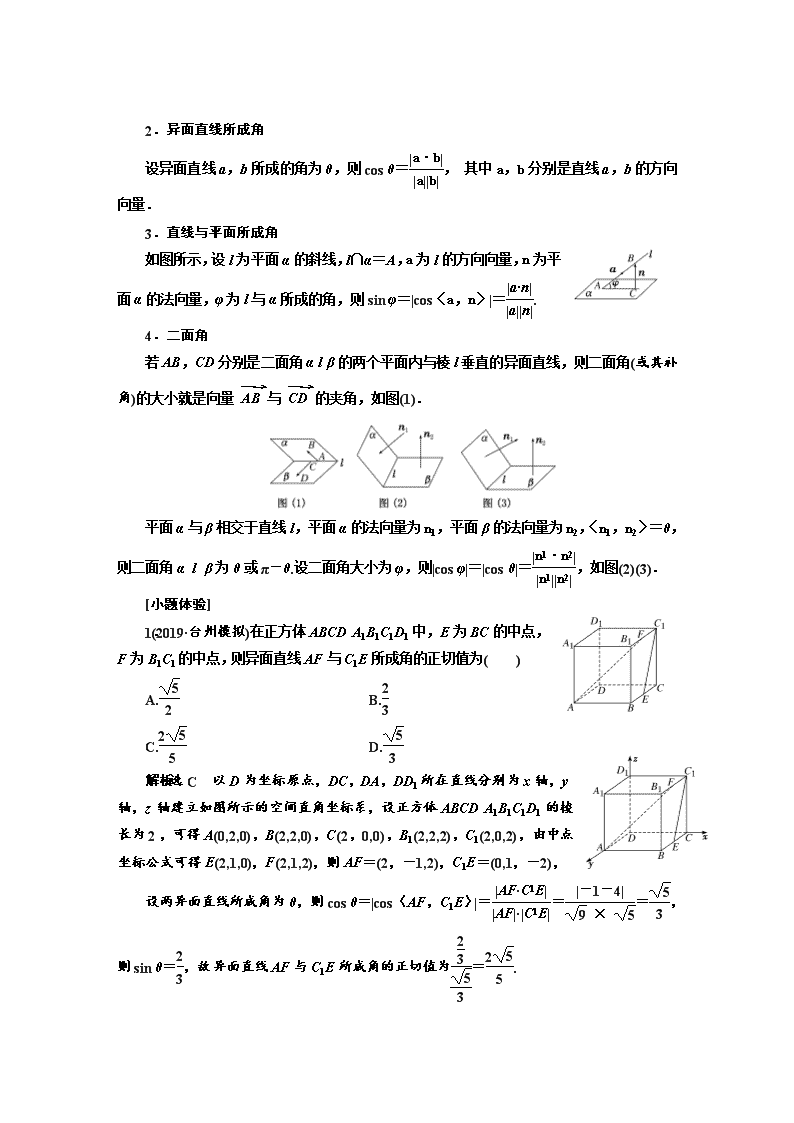
第六节立体几何中的向量方法 ‎1．空间向量的概念、数量积及坐标运算 ‎(1)空间向量及其相关概念 语言描述 共线向量(平行向量)‎ 表示空间向量的有向线段所在的直线互相平行或重合 共面向量 平行于同一个平面的向量 共线向量定理 对空间任意两个向量a，b(b≠0)，a∥b⇔存在λ∈R，使a＝λb 共面向量定理 若两个向量a，b不共线，则向量p与向量a，b共面⇔存在唯一的有序实数对(x，y)，使p＝xa＋yb 空间向量基本定理 定理：如果三个向量a，b，c不共面，那么对空间任一向量p，存在有序实数组{x，y，z}使得p＝x a＋y b＋z c 推论：设O，A，B，C是不共面的四点，则对平面ABC内任一点P都存在唯一的三个有序实数x，y，z，使＝x＋y＋z且x＋y＋z＝1‎ ‎(2)两个向量的数量积：‎ ‎①a·b＝|a||b|cos〈a，b〉；‎ ‎②a⊥b⇔a·b＝0(a，b为非零向量)；‎ ‎③|a|2＝a2，|a|＝.‎ ‎(3)向量的坐标运算：‎ a＝(a1，a2，a3)，b＝(b1，b2，b3)‎ 向量和 a＋b＝(a1＋b1，a2＋b2，a3＋b3)‎ 向量差 a－b＝(a1－b1，a2－b2，a3－b3)‎ 数量积 a·b＝a1b1＋a2b2＋a3b3‎ 共线 a∥b⇒a1＝λb1，a2＝λb2，a3＝λb3(λ∈R，b≠0)‎ 垂直 a⊥b⇔a1b1＋a2b2＋a3b3＝0‎ 夹角 公式 cos〈a，b〉＝ ‎2．异面直线所成角 设异面直线a，b所成的角为θ，则cos θ＝， 其中a，b分别是直线a，b的方向向量．‎ ‎3．直线与平面所成角 如图所示，设l为平面α的斜线，l∩α＝A，a为l的方向向量，n为平面α的法向量，φ为l与α所成的角，则sin φ＝|cos〈a，n〉|＝.‎ ‎4．二面角 ‎ 若AB，CD分别是二面角αlβ的两个平面内与棱l垂直的异面直线，则二面角(或其补角)的大小就是向量与的夹角，如图(1)．‎ 平面α与β相交于直线l，平面α的法向量为n1，平面β的法向量为n2，〈n1，n2〉＝θ，则二面角α l β为θ或π－θ.设二面角大小为φ，则|cos φ|＝|cos θ|＝，如图(2)(3)．‎ ‎[小题体验]‎ ‎1．(2019·台州模拟)在正方体ABCDA1B1C1D1中，E为BC的中点，F为B1C1的中点，则异面直线AF与C1E所成角的正切值为(　　)‎ A.　　　　　　　　　 B. C. D. 解析：选C　以D为坐标原点，DC，DA，DD1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，设正方体ABCDA1B1C1D1的棱长为2，可得A(0,2,0)，B(2,2,0)，C(2，0,0)，B1(2,2,2)，C1(2,0,2)，由中点坐标公式可得E(2,1,0)，F(2,1,2)，则AF＝(2，－1,2)，C1E＝(0,1，－2)，‎ 设两异面直线所成角为θ，则cos θ＝|cos〈AF，C1E〉|＝＝＝，则sin θ＝，故异面直线AF与C1E所成角的正切值为＝.‎ ‎2．(教材习题改编)已知a＝(2,3,1)，b＝(－4,2，x)，且a⊥b，则|b|＝________.‎ 答案：2 ‎3．已知正四棱锥S ABCD的侧棱长与底面边长都相等，E是SB的中点，则AE，SD所成角的余弦值为________．‎ 解析：以两对角线AC与BD的交点O作为原点，以OA，OB，OS所在直线分别为x轴，y轴，z轴建立空间直角坐标系，设边长为2，则有O(0，0,0)，A(，0,0)，B(0，，0)，S(0，0，)，D(0，－，0)，E，＝，＝(0，－，－)，|cos〈，〉|＝＝＝，故AE，SD所成角的余弦值为.‎ 答案： ‎4．(教材习题改编)在长方体ABCD A1B1C1D1中，AB＝2，BC＝AA1＝1，则D1C1与平面A1BC1所成角的正弦值为________．‎ 解析：如图，建立空间直角坐标系Dxyz，则D1(0,0,1)，C1(0,2,1)，A1(1,0,1)，B(1,2,0)，‎ ‎∴＝(0,2,0)，＝(－1,2,0)，＝(0,2，－1)，‎ 设平面A1BC1的一个法向量为n＝(x，y，z)，‎ 由 令y＝1，得n＝(2,1,2)，‎ 设D1C1与平面A1BC1所成角为θ，则 sin θ＝|cos〈，n〉|＝＝＝，‎ 即直线D1C1与平面A1BC1所成角的正弦值为.‎ 答案： ‎1．共线向量定理中a∥b⇔存在λ∈R，使a＝λb易忽视b≠0.‎ ‎2．一个平面的法向量有无数个，但要注意它们是共线向量，不要误认为是共面向量．‎ ‎3．求异面直线所成角时易忽视角的范围而导致结论错误．‎ ‎4．求直线与平面所成角时，注意求出夹角的余弦值的绝对值应为线面角的正弦值．‎ ‎5．利用平面的法向量求二面角的大小时，当求出两半平面α，β的法向量n1，n2时，要根据向量坐标在图形中观察法向量的方向，从而确定二面角与向量n1，n2的夹角是相等(‎ 一个平面的法向量指向二面角的内部，另一个平面的法向量指向二面角的外部)，还是互补(两个法向量同时指向二面角的内部或外部)，这是利用向量求二面角的难点、易错点．‎ ‎[小题纠偏]‎ ‎1．若平面π1，π2垂直，则下面可以是这两个平面的法向量的是(　　)‎ A．n1＝(1,2,1)，n2＝(－3,1,1)‎ B．n1＝(1,1,2)，n2＝(－2,1,1)‎ C．n1＝(1,1,1)，n2＝(－1,2,1)‎ D．n1＝(1,2,1)，n2＝(0，－2，－2)‎ 解析：选A　两个平面垂直时其法向量也垂直，只有A中的两个向量垂直．‎ ‎2．已知a＝(λ＋1,0,2)，b＝(6,2μ－1,2λ)，若a∥b，则λ与μ的值可以是(　　)‎ A．2，　　　　　　　　　 　B．－， C．－3,2 D．2,2‎ 解析：选A　∵a∥b，∴b＝ka，‎ 即(6,2μ－1,2λ)＝k(λ＋1,0,2)，‎ ‎∴解得或故选A.‎ ‎3．(2018·浙江高考原创卷)若在三棱柱ABCA1B1C1中，∠A1AC＝∠BAC＝60°，平面A1ACC1⊥平面ABC，AA1＝AC＝AB，则异面直线AC1与A1B所成角的余弦值为(　　)‎ A. B. C. D. 解析：选B　取AC的中点M，连接MB，MA1，易得MA，MB，MA1两两垂直．以M为坐标原点，MA，MB，MA1的方向分别为x轴，y轴，z轴的正方向建立如图所示的空间直角坐标系．设AA1＝AC＝AB＝2，则A(1,0,0)，B(0，，0)，A1(0,0，)，C1(－2,0，)，所以AC1＝(－3,0，)，A1B＝(0，，－)，所以cos〈AC1，A1B〉＝＝－，故异面直线AC1与A1B所成角的余弦值为.‎ ‎4．过正方形ABCD的顶点A作线段PA⊥平面ABCD，若AB＝PA，则平面ABP与平面CDP所成的二面角为________．‎ 解析：如图所示，建立空间直角坐标系，设AB＝PA＝1，知A(0,0,0)，B(1，0,0)，D(0,1,0)，C(1,1,0)，P(0，0,1)，由题意，AD⊥平面ABP，设E为PD的中点，连接AE，则AE⊥PD，又因为CD⊥平面 PAD，‎ 所以AE⊥CD，‎ 又PD∩CD＝D，所以AE⊥平面CDP.‎ 所以＝(0,1,0)，＝分别是平面ABP，平面CDP的法向量，且〈，〉＝45°，‎ 所以平面ABP与平面CDP所成的二面角为45°.‎ 答案：45°‎ 考点一　利用向量证明平行与垂直问题 ‎[典例引领]‎ 如图所示，在四棱锥P ABCD中，PC⊥平面ABCD，PC＝2，在四边形ABCD中，∠B＝∠C＝90°，AB＝4，CD＝1，点M在PB上，PB＝4PM，PB与平面ABCD成30°的角．求证：‎ ‎(1)CM∥平面PAD；‎ ‎(2)平面PAB⊥平面PAD.‎ 证明：以C为坐标原点，CB所在直线为x轴，CD所在直线为y轴，CP所在直线为z轴建立如图所示的空间直角坐标系C xyz.‎ ‎∵PC⊥平面ABCD，‎ ‎∴∠PBC为PB与平面ABCD所成的角，∴∠PBC＝30°，‎ ‎∵PC＝2，‎ ‎∴BC＝2，PB＝4，‎ ‎∴D(0,1,0)，B(2，0,0)，A(2，4,0)，P(0,0,2)，M，∴＝(0，－1,2)，＝(2，3,0)，‎ ＝.‎ ‎(1)设n＝(x，y，z)为平面PAD的一个法向量，‎ 由即 令y＝2，得n＝(－，2,1)．‎ ‎∵n·＝－×＋2×0＋1×＝0，‎ ‎∴n⊥.又CM⊄平面PAD，∴CM∥平面PAD.‎ ‎(2)法一：由(1)知＝(0,4,0)，＝(2，0，－2)，‎ 设平面PAB的一个法向量为m＝(x0，y0，z0)，‎ 由即 令x0＝1，得m＝(1,0，)，‎ 又∵平面PAD的一个法向量n＝(－，2,1)，‎ ‎∴m·n＝1×(－)＋0×2＋×1＝0，‎ ‎∴平面PAB⊥平面PAD.‎ 法二：取AP的中点E，连接BE，‎ 则E(，2,1)，＝(－，2,1)．‎ ‎∵PB＝AB，∴BE⊥PA.‎ 又∵·＝(－，2,1)·(2，3,0)＝0，‎ ‎∴⊥.∴BE⊥DA.‎ 又PA∩DA＝A，∴BE⊥平面PAD.‎ 又∵BE⊂平面PAB，∴平面PAB⊥平面PAD.‎ ‎[由题悟法]‎ ‎1．利用向量法证明平行问题的类型及方法 ‎(1)证明线线平行：两条直线的方向向量平行．‎ ‎(2)证明线面平行：‎ ‎①该直线的方向向量与平面的某一法向量垂直；‎ ‎②证明该直线的方向向量与平面内某直线的方向向量平行；‎ ‎③证明该直线的方向向量可以用平面内的两个不共线的向量线性表示．‎ ‎(3)证明面面平行：两个平面的法向量平行．‎ ‎2．利用向量法证明垂直问题的类型及方法 ‎(1)证明线线垂直：两条直线的方向向量的数量积为0.‎ ‎(2)证明线面垂直：直线的方向向量与平面的法向量平行．‎ ‎(3)证明面面垂直：‎ ‎①其中一个平面与另一个平面的法向量平行；‎ ‎②两个平面的法向量垂直．‎ ‎[即时应用]‎ ‎(2018·昆明两区七校调研)如图，在长方体ABCDA1B1C1D1中，AB＝AA1＝1，E为BC 中点．‎ ‎(1)求证：C1D⊥D1E；‎ ‎(2)在棱AA1上是否存在一点M，使得BM∥平面AD1E？若存在，求的值，若不存在，说明理由；‎ ‎(3)若二面角B1AED1的大小为90°，求AD的长．‎ 解：(1)证明：以D为原点，建立如图所示的空间直角坐标系Dxyz，设AD＝a，则D(0,0,0)，A(a,0,0)，B(a,1,0)，C(0,1,0)，B1(a,1,1)，C1(0,1,1)，D1(0，0,1)，E，‎ ‎∴＝(0，－1，－1)，＝，‎ 则·＝0，‎ ‎∴C1D⊥D1E.‎ ‎(2)设＝h，则M(a,0，h)，‎ ‎∴＝(0，－1，h)，＝，＝(－a,0,1)，‎ 设平面AD1E的法向量为n＝(x，y，z)，‎ 则 ‎∴平面AD1E的一个法向量为n＝(2，a,2a)，‎ ‎∵BM∥平面AD1E，‎ ‎∴⊥n，即·n＝2ah－a＝0，‎ ‎∴h＝.‎ 即在AA1上存在点M，使得BM∥平面AD1E，‎ 此时＝.‎ ‎(3)连接AB1，B1E，设平面B1AE的法向量为m＝(x′，y′，z′)，＝，＝(0,1,1)，‎ 则 ‎∴平面B1AE的一个法向量为m＝(2，a，－a)．‎ ‎∵二面角B1AED1的大小为90°，‎ ‎∴m⊥n，∴m·n＝4＋a2－2a2＝0，‎ ‎∵a＞0，∴a＝2，即AD＝2.‎ ‎[典例引领]‎ ‎(2018·浙江名校信息卷)如图1，在平面多边形ABCDE中，四边形ABCD是正方形，△ADE是正三角形．将△ADE所在平面沿直线AD折叠，使得点E达到点S的位置(如图2)．若二面角SADC的平面角θ∈，则异面直线AC与SD所成角的余弦值的取值范围是(　　)‎ A.　　　　　　　　　 B. C. D. 解析：选D　如图，取AD的中点O，BC的中点G，连接OS，OG，则OG⊥AD，以OG所在直线为x轴，OD所在直线为y轴，过点O且垂直于平面ABCD的直线为z轴，建立空间直角坐标系．设AB＝2，则A(0，－1,0)，C(2，1,0)，D(0,1,0)．因为△SAD为正三角形，O为AD的中点，所以SO⊥AD，又OG⊥AD，所以∠SOG是二面角SADC的平面角，即∠SOG＝θ，则S(cos θ，0，sin θ)．因为AC＝(2,2,0)，DS＝(cos θ，－1，sin θ)，所以cos〈AC，DS〉＝.又θ∈，所以cos θ∈，所以cos〈AC，DS〉∈，故异面直 线AC与SD所成角的余弦值的取值范围是.‎ ‎[由题悟法]‎ 用向量法求异面直线所成角的一般步骤 ‎(1)选择三条两两垂直的直线建立空间直角坐标系；‎ ‎(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；‎ ‎(3)利用向量的夹角公式求出向量夹角的余弦值；‎ ‎(4)两异面直线所成角的余弦等于两向量夹角余弦值的绝对值．‎ ‎[即时应用]‎ ‎ 如图，四面体ABCD中，O是BD的中点，CA＝CB＝CD＝BD＝2，AB＝AD＝.‎ ‎(1)求证：AO⊥平面BCD；‎ ‎(2)求异面直线AB与CD所成角的余弦值．‎ 解：(1)证明：连接OC，由CA＝CB＝CD＝BD＝2，AB＝AD＝，O是BD的中点，知CO＝，AO＝1，AO⊥BD.‎ 在△AOC中，AC2＝AO2＋OC2，则AO⊥OC.‎ 又BD∩OC＝O，因此AO⊥平面BCD.‎ ‎(2)如图建立空间直角坐标系Oxyz，则A(0,0,1)，B(1,0,0)，C(0，，0)，D(－1,0,0)，＝(1,0，－1)，＝(－1，－，0)，‎ ‎∴|cos〈，〉|＝＝.即异面直线AB与CD所成角的余弦值为.‎ ‎[典例引领]‎ ‎　(2018·浙江高考原创卷)如图，边长为3的菱形ABCD所在的平面与等腰直角三角形ABE所在的平面互相垂直，∠BAD＝60°，AE⊥BE，点M，N分别在AB，DE上，且＝＝.‎ ‎(1)求证：MN∥平面BCE；‎ ‎(2)求直线BC与平面CDE所成角的正弦值．‎ 解：(1)证明：∵菱形ABCD中∠BAD＝60°，且平面ABCD⊥平面ABE，∴点D在平面ABE内的射影恰好是AB的中点，设为O，连接OD，OE，又△ABE是等腰直角三角形，AE⊥BE，∴OE⊥AB.分别以OE，OB，OD所在的直线为x轴，y轴，z轴建立如图所示的空间直角坐标系Oxyz，‎ 易得，OE＝，OD＝，OM＝，‎ ‎∴E，M，D，B，C，‎ ‎∴EB＝，BC＝.‎ ‎∵EN＝2ND，∴N，∴MN＝，‎ ‎∴MN＝BC－EB，即MN，BC，EB共面，‎ 又MN⊄平面BCE，∴MN∥平面BCE.‎ ‎(2)设平面CDE的法向量为n＝(x，y，z)，‎ 由(1)得ED＝，DC＝(0,3,0)，‎ 则即 令z＝1，则n＝(，0,1)为平面CDE的一个法向量．‎ 设直线BC与平面CDE所成角的大小为θ，‎ 则sin θ＝|cos〈n，BC〉|＝＝＝，‎ ‎∴直线BC与平面CDE所成角的正弦值为.‎ ‎[由题悟法]‎ 向量法求线面角的2大途径 ‎(1)分别求出斜线和它所在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)．‎ ‎(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．‎ ‎[即时应用]‎ ‎(2018·宁波十校联考)如图，△ABC中，O是BC的中点，AB＝AC，AO＝2OC＝2.将△BAO沿AO折起，使B点到达B′点．‎ ‎(1)求证：AO⊥平面B′OC；‎ ‎(2)当三棱锥B′AOC的体积最大时，试问在线段B′A上是否存在一点P，使CP与平面B′OA所成的角的正弦值为？若存在，求出点P的位置；若不存在，请说明理由．‎ 解：(1)证明：因为AB＝AC且O是BC的中点，‎ 所以AO⊥BO，AO⊥CO，由折叠知AO⊥B′O，又CO∩B′O＝O，‎ 所以AO⊥平面B′OC. ‎ ‎(2)当B′O⊥平面AOC时，三棱锥B′AOC的体积最大，所以OA，OB′，OC两两垂直，如图建立空间直角坐标系Oxyz，‎ 则A(2,0,0)，B′(0,0,1)，C(0,1,0)‎ 设＝λ＝(－2λ，0，λ)，‎ 则＝＋＝(2－2λ，－1，λ), ‎ 又平面B′OA的法向量n＝(0,1,0)，‎ 依题意得，＝，‎ 即＝，化简得，10λ2－16λ＋7＝0, ‎ 此方程无解，所以满足条件的点P不存在. ‎ ‎[典例引领]‎ ‎(2018·宁波一模)如图，在空间直角坐标系Oxyz中，正四面体(各条棱的长均相等的三棱锥)ABCD的顶点A，B，C分别在x轴，y轴，z轴上．‎ ‎(1)求证：CD∥平面OAB；‎ ‎(2)求二面角CABD的余弦值．‎ 解：(1)证明：由已知可得OA＝OB＝OC.‎ 设OA＝a(a＞0)，‎ 则AB＝a，O(0,0,0)，A(a,0,0)，B(0，a,0)，C(0,0，a)，‎ 设D点的坐标为(x，y，z)(x，y，z均大于0)，‎ 则由DA＝DB＝DC＝a，‎ 可得(x－a)2＋y2＋z2＝x2＋(y－a)2＋z2＝x2＋y2＋(z－a)2＝2a2，‎ 解得x＝y＝z＝a，即D(a，a，a)，‎ ‎∴CD＝(a，a,0)．‎ 又平面OAB的一个法向量为OC＝(0,0，a)，‎ ‎∴CD·OC＝0，即CD⊥OC，‎ ‎∵CD⊄平面OAB，∴CD∥平面OAB.‎ ‎(2)设F为AB的中点，‎ 连接CF，DF，‎ 则CF⊥AB，DF⊥AB，‎ 则∠CFD为二面角CABD的平面角．‎ 由(1)知，在△CFD中，‎ CF＝DF＝a×＝a，CD＝a，‎ 则由余弦定理，‎ 得cos∠CFD＝＝，‎ 结合图形知，二面角CABD为锐角，故二面角CABD的余弦值为.‎ ‎[由题悟法]‎ 利用法向量求二面角时的2个注意点 ‎(1)对于某些平面的法向量要注意题中隐含条件，不用单独求．‎ ‎(2)注意判断二面角的平面角是锐角还是钝角，可结合图形进行，以防结论失误．‎ ‎[即时应用]‎ ‎(2018·金丽衢十二校联考)在几何体ABCDE中，矩形BCDE的边CD＝2，BC＝AB＝1，∠ABC＝90°，直线EB⊥平面ABC，P是线段AD上的点，且AP＝2PD，M为线段AC的中点．‎ ‎(1)证明：BM∥平面ECP；‎ ‎(2)求二面角AECP的余弦值．‎ 解：(1)证明：连接BD，MD，BD∩CE＝F，MD∩CP＝N，连接FN. ‎ ‎∵四边形BCDE为矩形，∴F为BD中点．‎ ‎∵EB⊥平面ABC，∴DC⊥平面ABC，‎ 如图，在直角△ACD中，取AP中点Q，连接QM，‎ ‎∵M是AC的中点，∴QM∥CP，‎ 又∵AP＝2PD，∴QP＝PD，‎ ‎∴DN＝MN，∴FN∥BM.‎ 又∵FN⊂平面ECP，而BM⊄平面ECP，‎ ‎∴BM∥平面ECP.‎ ‎(2)如图，以B点为原点，BA所在的直线为x轴，BC所在的直线为y轴，BE所在的直线为z轴，建立空间直角坐标系，则B(0,0,0), A(1,0,0), C(0，1,0), E(0,0,2), ‎ P.‎ ＝(－1,1,0)，＝(－1,0,2)，‎ ＝，＝.‎ 设平面ACE的法向量为n1＝(x1，y1，z1)，‎ 则有 令x1＝2，得n1＝(2,2,1)；‎ 设平面PCE法向量n2＝(x2，y2，z2)，‎ 则有 令y2＝2，得n2＝(－2,2,1). ‎ ‎∴cosn1，n2＝＝.‎ 由图知，二面角AECP为锐角，‎ ‎∴二面角AECP的余弦值为.‎ 一抓基础，多练小题做到眼疾手快 ‎1．若直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则(　　)‎ A．l∥α　　　　　　　　　 　B．l⊥α C．l⊂α D．l与α斜交 解析：选B　∵a＝(1,0,2)，n＝(－2,0，－4)，∴n＝－2a，‎ 即a∥n，∴l⊥α.‎ ‎2．(2018·嘉兴模拟)已知A(4,1,3)，B(2，－5,1)，C(3,7，－5)，则平行四边形ABCD的顶点D的坐标是(　　)‎ A．(2,4，－1) B．(2,3,1)‎ C．(－3,1,5) D．(5,13，－3)‎ 解析：选D　由题意知，＝(－2，－6，－2)，设点D(x，y，z)，则＝(3－x,7－y，－5－z)，因为＝，所以x＝5，y＝13，z＝－3，故选D.‎ ‎3．(2018·舟山模拟)已知A(1,0,0)，B(0，－1,1)，O为坐标原点，＋λ与的夹角为120°，则λ的值为(　　)‎ A．± B. C．－ D．± 解析：选C　因为＋λ＝(1，－λ，λ)，‎ 所以cos 120°＝＝－，解得λ＝－.‎ ‎4．若平面α的一个法向量为u1＝(－3，y,2)，平面β的一个法向量为u2＝(6，－2，z)，且α∥β，则y＋z＝________.‎ 解析：因为α∥β，所以u1∥u2，所以＝＝，‎ 所以y＝1，z＝－4，所以y＋z＝－3.‎ 答案：－3‎ ‎5．(2019·绍兴质检)如图，60°的二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB＝4，AC＝6，BD＝8，则CD的长为________．‎ 解析：∵60°的二面角的棱上有A，B两点，AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，‎ ‎∴CD＝CA＋AB＋BD，CA·AB＝0，AB·BD＝0，‎ ‎∵AB＝4，AC＝6，BD＝8，‎ ‎∴CD2＝(CA＋AB＋BD)2‎ ‎＝CA2＋AB2＋BD2＋2CA·BD ‎＝36＋16＋64＋2×6×8×cos 120°‎ ‎＝68，‎ ‎∴CD的长为2.‎ 答案：2 ‎6．已知V为矩形ABCD所在平面外一点，且VA＝VB＝VC＝VD，＝，＝，＝.则VA与平面PMN的位置关系是________．‎ 解析：如图，设＝a，＝b，＝c，则＝a＋c－b，‎ 由题意知＝b－c，‎ ＝－ ‎＝a－b＋c.‎ 因此＝＋，‎ ‎∴，，共面．‎ 又∵VA⊄平面PMN，∴VA∥平面PMN.‎ 答案：平行 二保高考，全练题型做到高考达标 ‎1.如图，在多面体ABC A1B1C1中，四边形A1ABB1是正方形，AB＝AC，BC＝AB，B1C1綊BC，二面角A1 AB C是直二面角．‎ 求证：(1)A1B1⊥平面AA1C；‎ ‎(2)AB1∥平面A1C1C.‎ 证明：∵二面角A1 AB C是直二面角，四边形A1ABB1为正方形，∴AA1⊥平面ABC.‎ 又∵AB＝AC，BC＝AB，∴∠CAB＝90°，‎ 即CA⊥AB，∴AB，AC，AA1两两互相垂直．‎ 建立如图所示的空间直角坐标系A xyz，‎ 设AB＝2，则A(0,0,0)，B1(0,2,2)，‎ A1(0,0,2)，C(2,0,0)，C1(1,1,2)．‎ ‎(1) ＝(0,2,0)，＝(0,0，－2)，＝(2,0,0)，设平面AA1C的一个法向量n＝(x，y，z)，‎ 则即 即取y＝1，则n＝(0,1,0)．‎ ‎∴＝2n，即∥n.∴A1B1⊥平面AA1C.‎ ‎(2)易知＝(0,2,2)，＝(1,1,0)，＝(2,0，－2)，‎ 设平面A1C1C的一个法向量m＝(x1，y1，z1)，‎ 则即 令x1＝1，则y1＝－1，z1＝1，即m＝(1，－1,1)．‎ ‎∴·m＝0×1＋2×(－1)＋2×1＝0，‎ ‎∴⊥m.又AB1⊄平面A1C1C，‎ ‎∴AB1∥平面A1C1C.‎ ‎2．(2018·浙江名校联考)如图，在直三棱柱ADFBCE中，AB＝BC＝BE＝2，CE＝2，点K在线段BE上．‎ ‎(1)求证：AC⊥平面BDE；‎ ‎(2)若EB＝4EK，求直线AK与平面BDF所成角φ的正弦值．‎ 解：(1)证明：在直三棱柱ADFBCE中，‎ AB⊥平面BCE，因为BE⊂平面BCE，BC⊂平面BCE，‎ 所以AB⊥BE，AB⊥BC.‎ 又AB＝BC＝BE＝2，CE＝2，‎ 所以BC2＋BE2＝CE2，且AC⊥BD，‎ 所以BE⊥BC.‎ 因为AB∩BC＝B，所以BE⊥平面ABCD.‎ 因为AC⊂平面ABCD，所以BE⊥AC.‎ 又BD∩BE＝B，所以AC⊥平面BDE.‎ ‎(2)法一：设AK交BF于点N，由(1)知，AB，AF，AD两两垂直且长度都为2，所以△BDF是边长为2的正三角形，所以点A在平面BDF内的射影M为△BDF的中心．连接MN，MF，AM，如图所示，则∠ANM为直线AK与平面BDF所成的角φ.‎ 又FM＝××2＝，‎ 所以AM＝＝ ＝.‎ 因为EB＝4EK，所以BK＝，‎ 所以AK＝＝ ＝.‎ 因为＝，所以＝，‎ 即＝，解得AN＝.‎ 在Rt△ANM中，sin φ＝＝＝.‎ 所以直线AK与平面BDF所成角φ的正弦值为.‎ 法二：由(1)知，AB，BC，BE两两垂直，以B为坐标原点，BC，BA，BE的方向分别为x轴、y轴、z轴的正方向，建立如图所示的空间直角坐标系，‎ 则B(0,0,0)，F(0,2,2)，A(0,2,0)，D(2，2,0)，BD＝(2,2,0)，BF＝(0,2,2)．‎ 因为EB＝4EK，所以K，‎ 所以AK＝.‎ 设平面BDF的法向量为n＝(x，y，z)，‎ 则即 取x＝1，则n＝(1，－1,1)为平面BDF的一个法向量．‎ 于是sin φ＝|cos〈n，AK〉|＝＝＝，‎ 所以直线AK与平面BDF所成角φ的正弦值为.‎ ‎3．(2018·浙江名校联考)已知长方形ABCD中，AB＝1，AD＝.现将长方形沿对角线BD折起，使AC＝a，得到一个四面体ABCD，如图所示．‎ ‎(1)试问：在折叠的过程中，异面直线AB与CD，AD与BC能否垂直？若能垂直，求出相应的a值；若不垂直，请说明理由．‎ ‎(2)当四面体ABCD的体积最大时，求二面角ACDB的余弦值．‎ 解：(1)若AB⊥CD，因为AB⊥AD，AD∩CD＝D，‎ 所以AB⊥平面ACD，所以AB⊥AC.‎ 即AB2＋a2＝BC2，即12＋a2＝()2，所以a＝1.‎ 若AD⊥BC，因为AD⊥AB，AB∩BC＝B，‎ 所以AD⊥平面ABC，所以AD⊥AC.‎ 即AD2＋a2＝CD2，即()2＋a2＝12，所以a2＝－1，无解．‎ 故AD⊥BC不成立．‎ ‎(2)要使四面体ABCD的体积最大，‎ 因为△BCD的面积为定值，‎ 所以只需三棱锥ABCD的高最大即可，此时平面ABD⊥平面BCD，过点A作AO⊥BD于点O，则AO⊥平面BCD，‎ 以O为原点建立空间直角坐标系Oxyz(如图)，‎ 则易知A，‎ C，D，‎ 显然，平面BCD的一个法向量为＝.‎ 设平面ACD的法向量为n＝(x，y，z)．‎ 因为＝，＝，‎ 所以令y＝，得n＝(1，，2)．‎ 故cos 〈，n〉＝＝.‎ 所以二面角ACDB的余弦值为.‎ ‎4．如图，在四棱锥SABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB＝BC＝2，CD＝SD＝1.‎ ‎(1)证明：SD⊥平面SAB；‎ ‎(2)求AB与平面SBC所成角的正弦值．‎ 解：(1)证明：以C为坐标原点，射线CD为x轴正半轴建立如图所示的空间直角坐标系Cxyz，则D(1,0,0)，A(2,2,0)，B(0,2,0)．‎ 设S(x，y，z)，显然x＞0，y＞0，z＞0，‎ 则＝(x－2，y－2，z)，＝(x，y－2，z)，＝(x－1，y，z)．‎ 由||＝||，得 ‎＝ ，解得x＝1.‎ 由||＝1，得y2＋z2＝1.①‎ 由||＝2，得y2＋z2－4y＋1＝0.②‎ 由①②，解得y＝，z＝.‎ ‎∴S，＝，＝，＝，‎ ‎∴·＝0，·＝0，∴DS⊥AS，DS⊥BS，‎ 又AS∩BS＝S，∴SD⊥平面SAB.‎ ‎(2)设平面SBC的法向量为n＝(x1，y1，z1)，‎ 则n⊥，n⊥，∴n·＝0，n·＝0.‎ 又＝，＝(0,2,0)，‎ ‎∴取z1＝2，得n＝(－，0,2)．‎ ‎∵＝(－2,0,0)，‎ ‎∴cos〈，n〉＝＝＝.‎ 故AB与平面SBC所成角的正弦值为.‎ 三上台阶，自主选做志在冲刺名校 ‎1.如图所示，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD＝NB＝1，E为BC的中点．‎ ‎(1)求异面直线NE与AM所成角的余弦值；‎ ‎(2)在线段AN上是否存在点S，使得ES⊥平面AMN？若存在，求线段AS的长；若不存在，请说明理由．‎ 解：(1)如图，以D为坐标原点，建立空间直角坐标系Dxyz.‎ 依题易得D(0,0,0)，A(1,0,0)，M(0,0,1)，C(0,1,0)，B(1,1,0)，N(1,1,1)，E，所以＝，＝(－1,0,1)．‎ 设异面直线NE与AM所成的角为θ，‎ 则cos θ＝|cos〈，〉|＝＝＝.‎ 所以异面直线NE与AM所成角的余弦值为.‎ ‎(2)假设在线段AN上存在点S，使得ES⊥平面AMN，‎ 因为＝(0,1,1)，可设＝λ＝(0，λ，λ)，λ∈[0,1]，又＝，‎ 所以＝＋＝.‎ 由ES⊥平面AMN，‎ 得即解得λ＝，此时＝，||＝.‎ 经检验，当AS＝时，ES⊥平面AMN.‎ 故线段AN上存在点S，使得ES⊥平面AMN，‎ 此时AS＝.‎ ‎2．(2019·杭二模拟)如图，在直三棱柱ABCA1B1C1中，AC＝AA1＝2，D为棱CC1的中点，AB1∩A1B＝O.‎ ‎(1)求证：C1O∥平面ABD；‎ ‎(2)设二面角DABC的正切值为，AC⊥BC，E为线段A1B上一点，且直线CE与平面ABD所成角的正弦值为，求.‎ 解：(1)证明：取AB的中点F，连接OF，DF，‎ 易知四边形ABB1A1为矩形，‎ ‎∴O为AB1的中点，‎ ‎∴OF∥BB1，OF＝BB1，‎ 又C1D∥BB1，C1D＝BB1，‎ ‎∴OF∥C1D，OF＝C1D，‎ ‎∴四边形OFDC1为平行四边形，∴C1O∥DF，‎ ‎∵C1O⊄平面ABD，DF⊂平面ABD，‎ ‎∴C1O∥平面ABD.‎ ‎(2)过C作CH⊥AB于H，连接DH，‎ 易知∠DHC为二面角DABC的平面角，‎ ‎∵DC＝1，tan∠DHC＝，∴CH＝，‎ 又AC＝2，AH⊥CH，∴∠HAC＝45°，‎ ‎∵AC⊥BC，∴BC＝AC＝2.‎ 以C为坐标原点，CA，CB，CC1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系Cxyz，‎ 其中C(0,0,0)，A(2,0,0)，B(0,2,0)，D(0,0,1)，A1(2,0,2)，‎ 则AB＝(－2,2,0)，BD＝(0，－2,1)，BA1＝(2，－2,2)，CB＝(0,2,0)．‎ 设平面ABD的法向量为n＝(x，y，z)，‎ 则取y＝1，可得平面ABD的一个法向量为n＝(1,1,2)．‎ 设BE＝λBA1 (0≤λ≤1)，‎ 则CE＝CB＋λBA1＝(2λ，2－2λ，2λ)，‎ ‎∴直线CE与平面ABD所成角的正弦值等于|cos〈CE，n〉|＝＝，∴36λ2－44λ＋13＝0，‎ 解得λ＝或λ＝，即＝或＝.‎ 命题点　向量法求空间角及应用 ‎1．(2018·全国卷Ⅱ)如图，在三棱锥PABC 中，AB＝BC＝2，PA＝PB＝PC＝AC＝4，O为AC的中点．‎ ‎(1)证明：PO⊥平面ABC；‎ ‎(2)若点M在棱BC上，且二面角MPAC为30°，求PC与平面PAM所成角的正弦值．‎ 解：(1)证明：因为PA＝PC＝AC＝4，O为AC的中点，‎ 所以PO⊥AC，且PO＝2.‎ 连接OB，因为AB＝BC＝AC，‎ 所以△ABC为等腰直角三角形，‎ 且OB⊥AC，OB＝AC＝2.‎ 所以PO＋OB2＝PB2，所以PO⊥OB.‎ 又因为OB∩AC＝O，‎ 所以PO⊥平面ABC.‎ ‎(2)以O为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系Oxyz.由已知得O(0,0,0)，B(2,0,0)，A(0，－2,0)，C(0，2,0)，P(0,0,2)，‎ ＝(0,2,2)．‎ 取平面PAC的一个法向量＝(2,0,0)．‎ 设M(a,2－a,0)(0＜a≤2)，则＝(a,4－a,0)．‎ 设平面PAM的法向量为n＝(x，y，z)，‎ 由得 令y＝a，得z＝－a，x＝(a－4)，‎ 所以平面PAM的一个法向量为n＝((a－4)，a，－a)，‎ 所以cos〈，n〉＝.‎ 由已知可得|cos〈，n〉|＝cos 30°＝，‎ 所以＝，‎ 解得a＝或a＝－4(舍去)．‎ 所以n＝.‎ 又＝(0,2，－2)，‎ 所以cos〈，n〉＝＝.‎ 所以PC与平面PAM所成角的正弦值为.‎ ‎2.(2018·全国卷Ⅰ)如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.‎ ‎(1)证明：平面PEF⊥平面ABFD；‎ ‎(2)求DP与平面ABFD所成角的正弦值．‎ 解：(1)证明：由已知可得BF⊥PF，BF⊥EF，‎ 又PF∩EF＝F，‎ 所以BF⊥平面PEF.‎ 又BF⊂平面ABFD，‎ 所以平面PEF⊥平面ABFD.‎ ‎(2)如图，作PH⊥EF，垂足为H.‎ 由(1)得，PH⊥平面ABFD.‎ 以H为坐标原点，，HP 的方向分别为y轴，z轴正方向，|‎ |为单位长，建立如图所示的空间直角坐标系Hxyz.‎ 由(1)可得，DE⊥PE.‎ 又DP＝2，DE＝1，‎ 所以PE＝.‎ 又PF＝1，EF＝2，所以PE⊥PF.‎ 所以PH＝，EH＝.‎ 则H(0,0,0)，P，D，‎ ＝，＝.‎ 又为平面ABFD的法向量，‎ 设DP与平面ABFD所成角为θ，‎ 则sin θ＝＝＝.‎ 所以DP与平面ABFD所成角的正弦值为.‎ ‎3.(2018·浙江高考)如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC＝120°，A1A＝4，C1C＝1，AB＝BC＝B1B＝2.‎ ‎(1)证明：AB1⊥平面A1B1C1；‎ ‎(2)求直线AC1与平面ABB1所成的角的正弦值．‎ 解：法一：(1)证明：由AB＝2，AA1＝4，BB1＝2，‎ AA1⊥AB，BB1⊥AB，得AB1＝A1B1＝2，‎ 所以A1B＋AB＝AA，‎ 故AB1⊥A1B1.‎ 由BC＝2，BB1＝2，CC1＝1，BB1⊥BC，CC1⊥BC，‎ 得B1C1＝.‎ 由AB＝BC＝2，∠ABC＝120°，得AC＝2.‎ 由CC1⊥AC，得AC1＝，‎ 所以AB＋B1C＝AC，‎ 故AB1⊥B1C1.‎ 又因为A1B1∩B1C1＝B1，‎ 所以AB1⊥平面A1B1C1.‎ ‎(2)如图，过点C1作C1D⊥A1B1，‎ 交直线A1B1于点D，连接AD.‎ 因为AB1⊥平面A1B1C1，‎ AB1⊂平面ABB1，‎ 所以平面A1B1C1⊥平面ABB1.‎ 因为平面A1B1C1∩平面ABB1＝A1B1，C1D⊥A1B1，C1D⊂平面A1B1C1，所以C1D⊥平面ABB1.‎ 所以∠C1AD是直线AC1与平面ABB1所成的角．‎ 由B1C1＝，A1B1＝2，A1C1＝，‎ 得cos∠C1A1B1＝，sin∠C1A1B1＝，‎ 所以C1D＝，‎ 故sin∠C1AD＝＝.‎ 所以直线AC1与平面ABB1所成的角的正弦值是.‎ 法二：(1)证明：以AC的中点O为坐标原点，分别以射线OB，OC为x轴，y轴的正半轴，建立如图所示的空间直角坐标系Oxyz.‎ 由题意知各点坐标如下：‎ A(0，－，0)，B(1,0,0)，A1(0，－，4)，B1(1,0,2)，C1(0，，1)．‎ 因此＝(1，，2)，＝(1，，－2)，＝(0,2，－3)．‎ 由·＝0，得AB1⊥A1B1.‎ 由·＝0，得AB1⊥A1C1.‎ 又因为A1B1∩A1C1＝A1，‎ 所以AB1⊥平面A1B1C1.‎ ‎(2)设直线AC1与平面ABB1所成的角为θ.‎ 由(1)可知＝(0,2，1)，＝(1，，0)，‎ ＝(0,0,2)．‎ 设平面ABB1的法向量为n＝(x，y，z)，‎ 由得 可取n＝(－，1,0)．‎ 所以sin θ＝|cos〈，n〉|＝＝.‎ 所以直线AC1与平面ABB1所成的角的正弦值是.‎ ‎4．(2018·北京高考)如图，在三棱柱ABCA1B1C1中，CC1⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB＝BC＝，AC＝AA1＝2.‎ ‎(1)求证：AC⊥平面BEF；‎ ‎(2)求二面角B CDC1的余弦值；‎ ‎(3)证明：直线FG与平面BCD相交．‎ 解：(1)证明：在三棱柱ABCA1B1C1中，‎ 因为CC1⊥平面ABC，AC⊂平面ABC，所以CC1⊥AC，‎ 所以四边形A1ACC1为矩形．‎ 又E，F分别为AC，A1C1的中点，‎ 所以AC⊥EF.‎ 因为AB＝BC，所以AC⊥BE.‎ 因为EF∩BE＝E，所以AC⊥平面BEF.‎ ‎(2)由(1)知AC⊥EF，AC⊥BE，EF∥CC1.‎ 又CC1⊥平面ABC，‎ 所以EF⊥平面ABC.‎ 因为BE⊂平面ABC，‎ 所以EF⊥BE.‎ 以E为坐标原点，EA，EB，EF所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系Exyz.‎ 由题意得B(0,2,0)，C(－1,0,0)，D(1，0,1)，E(0,0,0)，F(0,0,2)，G(0，2,1)．‎ 所以＝(－1，－2,0)，‎ ＝(1，－2,1)．‎ 设平面BCD的一个法向量为n＝(x0，y0，z0)，‎ 则即 令y0＝－1，则x0＝2，z0＝－4.‎ 于是n＝(2，－1，－4)．‎ 又平面CC1D的一个法向量为＝(0,2,0)，‎ 所以cos〈n，〉＝＝－.‎ 由图知二面角BCDC1为钝角，‎ 所以其余弦值为－.‎ ‎(3)证明：由(2)知平面BCD的法向量为n＝(2，－1，－4)，‎ ＝(0,2，－1)．‎ 因为n·＝2×0＋(－1)×2＋(－4)×(－1)＝2≠0，‎ 所以直线FG与平面BCD相交．‎ ‎5．(2018·天津高考)如图，AD∥BC且AD＝2BC，AD⊥CD，EG∥AD且EG＝AD，CD∥FG且CD＝2FG，DG⊥平面ABCD，DA＝DC＝DG＝2.‎ ‎(1)若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；‎ ‎(2)求二面角EBCF的正弦值；‎ ‎(3)若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长．‎ 解：依题意，可以建立以D为坐标原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系(如图)，则D(0,0,0)，A(2,0,0)，B(1,2,0)，C(0,2,0)，E(2,0,2)，F(0，1,2)，G(0,0,2)，M，N(1,0,2)．‎ ‎(1)证明：依题意得＝(0,2,0)，＝(2,0,2)．‎ 设n1＝(x1，y1，z1)为平面CDE的法向量，‎ 则即 不妨令z1＝－1，可得n1＝(1,0，－1)．‎ 又＝，可得·n1＝0.‎ 因为直线MN⊄平面CDE，‎ 所以MN∥平面CDE.‎ ‎(2)依题意，可得＝(－1,0,0)，＝(1，－2,2)，‎ ＝(0，－1,2)．‎ 设n2＝(x2，y2，z2)为平面BCE的法向量，‎ 则即 不妨令z2＝1，可得n2＝(0,1,1)．‎ 设n3＝(x3，y3，z3)为平面BCF的法向量，‎ 则即 不妨令z3＝1，可得n3＝(0,2,1)．‎ 因此有cos〈n2，n3〉＝＝＝，‎ 于是sin〈n2，n3〉＝.‎ 所以二面角EBCF的正弦值为.‎ ‎(3)设线段DP的长为h(h∈[0,2])，‎ 则点P的坐标为(0,0，h)，可得＝(－1，－2，h)．‎ 易知＝(0,2,0)为平面ADGE的一个法向量，‎ 故|cos〈，〉|＝＝ .‎ 由题意，可得＝sin 60°＝，‎ 解得h＝∈[0,2]．‎ 所以线段DP的长为.‎