【数学】2020届北京一轮复习通用版9-7圆锥曲线的综合问题作业
9.7 圆锥曲线的综合问题
挖命题
【考情探究】
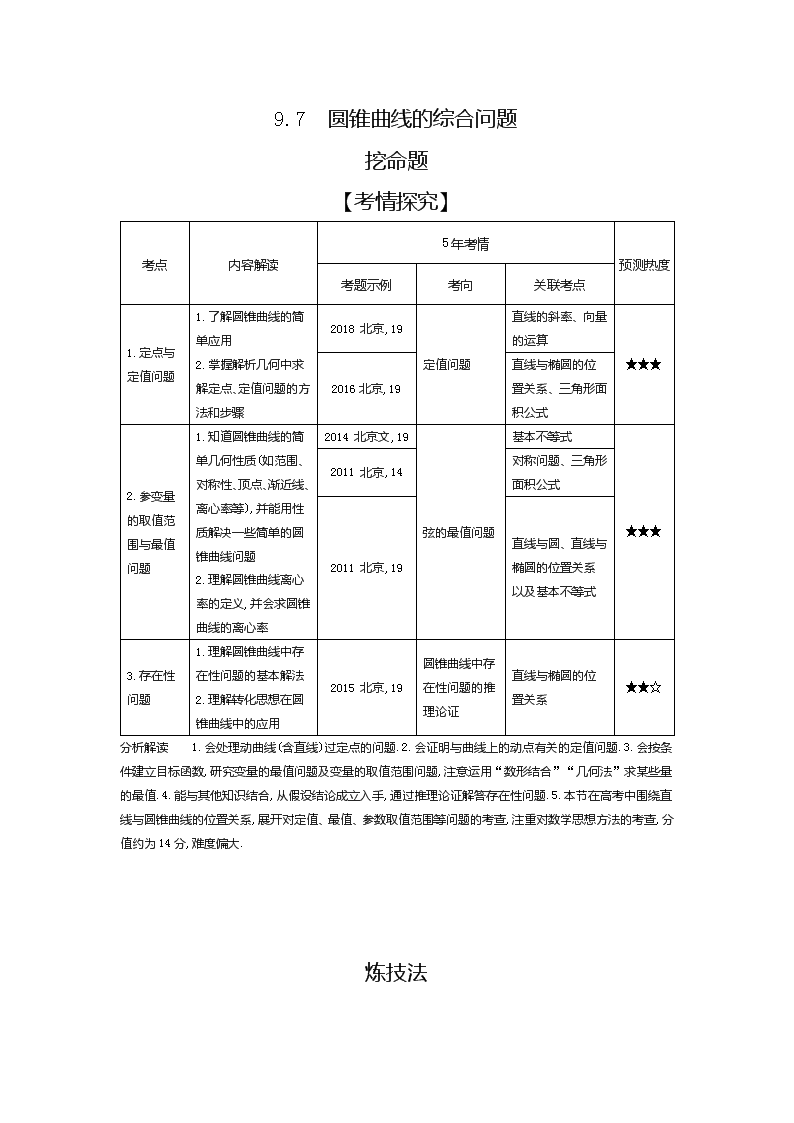
考点
内容解读
5年考情
预测热度
考题示例
考向
关联考点
1.定点与定值问题
1.了解圆锥曲线的简单应用
2.掌握解析几何中求解定点、定值问题的方法和步骤
2018 北京,19
定值问题
直线的斜率、向量的运算
★★★
2016北京,19
直线与椭圆的位置关系、三角形面积公式
2.参变量的取值范围与最值问题
1.知道圆锥曲线的简单几何性质(如范围、对称性、顶点、渐近线、离心率等),并能用性质解决一些简单的圆锥曲线问题
2.理解圆锥曲线离心率的定义,并会求圆锥曲线的离心率
2014 北京文,19
弦的最值问题
基本不等式
★★★
2011 北京,14
对称问题、三角形面积公式
2011 北京,19
直线与圆、直线与椭圆的位置关系以及基本不等式
3.存在性问题
1.理解圆锥曲线中存在性问题的基本解法
2.理解转化思想在圆锥曲线中的应用
2015 北京,19
圆锥曲线中存在性问题的推理论证
直线与椭圆的位置关系
★★☆
分析解读 1.会处理动曲线(含直线)过定点的问题.2.会证明与曲线上的动点有关的定值问题.3.会按条件建立目标函数,研究变量的最值问题及变量的取值范围问题,注意运用“数形结合”“几何法”求某些量的最值.4.能与其他知识结合,从假设结论成立入手,通过推理论证解答存在性问题.5.本节在高考中围绕直线与圆锥曲线的位置关系,展开对定值、最值、参数取值范围等问题的考查,注重对数学思想方法的考查,分值约为14分,难度偏大.
炼技法
【方法集训】
方法1 与圆锥曲线相关的最值、范围问题的解题方法
1.已知椭圆W:x2a2+y2b2=1(a>b>0)的左右焦点分别为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=23.
(1)求椭圆W的标准方程及离心率;
(2)如图,过点F1作直线l1与椭圆W交于点A,C,过点F2作直线l2⊥l1,且l2与椭圆W交于点B,D,l1与l2交于点E,试求四边形ABCD面积的最大值.
解析 (1)由已知,得2c=2,2a=23,a2=b2+c2,解得c=1,a=3,b=2.
所以椭圆W的标准方程为x23+y22=1,离心率e=ca=33.
(2)连接EO.
由题意知EF1⊥EF2,O为F1F2的中点,所以|EO|=12|F1F2|=1.
所以E点轨迹是以原点为圆心,1为半径的圆.
显然E点在椭圆W的内部.
S四边形ABCD=S△ABC+S△ADC=12|AC|·|BE|+12|AC|·|DE|=12|AC|·|BD|.
当直线l1,l2中一条与x轴垂直时,不妨令l2⊥x轴,此时AC为长轴,BD⊥x轴,把x=1代入椭圆方程,可求得y=±233,
则|BD|=433,
此时S四边形ABCD=12|AC|·|BD|=4.
当直线l1,l2的斜率都存在时,设直线l1:x=my-1(m≠0),A(x1,y1),C(x2,y2).
联立x=my-1,x23+y22=1,消去x,得(2m2+3)y2-4my-4=0.
所以y1+y2=4m2m2+3,y1y2=-42m2+3,
则|AC|=(1+m2)(y1-y2)2=43(m2+1)2m2+3.
同理,|BD|=43(m2+1)2+3m2.
S四边形ABCD=12|AC|·|BD|=12·43(m2+1)2m2+3·43(m2+1)2+3m2=24(m2+1)2(2m2+3)(3m2+2)
=24(m4+2m2+1)6m4+13m2+6=4(6m4+12m2+6)6m4+13m2+6=41-m26m4+13m2+6<4.
综上,四边形ABCD面积的最大值为4.
思路分析 (1)由椭圆定义及焦距|F1F2|=2c=2,求得a、b和c的值,即可求得椭圆的方程及离心率.
(2)当有一条直线斜率不存在时,有S四边形ABCD=12|AC|·|BD|=4.当直线斜率存在时,设直线l1的方程,代入椭圆方程,由根与系数的关系及弦长公式求得|AC|,同理求得|BD|,表示出四边形ABCD的面积,即可求得四边形ABCD面积的取值范围,再求最大值.
2.过点A(1,0)的直线l与椭圆C:x23+y2=1相交于E,F两点,自E,F分别向直线x=3作垂线,垂足分别为E1,F1.
(1)当直线l的斜率为1时,求线段EF的中点坐标;
(2)记△AEE1,△AFF1的面积分别为S1,S2.设λ=S1S2,求λ的取值范围.
解析 (1)依题意,得直线l的方程为y=x-1,由y=x-1,x2+3y2-3=0,得2x2-3x=0.
设E(x1,y1),F(x2,y2),线段EF的中点为M(x0,y0),
则x1+x2=32,则x0=34,
y0=x0-1=-14.
所以M34,-14.
(2)当直线l与x轴重合时,△AEE1和AFF1不存在.
设直线l的方程为x=my+1,由x=my+1,x2+3y2-3=0,
得(m2+3)y2+2my-2=0,显然m∈R.
设E(x1,y1),F(x2,y2),则E1(3,y1),F1(3,y2).
则y1+y2=-2mm2+3,y1y2=-2m2+3.
因为λ=S1S2=12(3-x1)|y1|·12(3-x2)|y2|
=14(2-my1)(2-my2)|y1y2|,
所以将y1+y2,y1y2的值代入上式,得
S1S2=14[4-2m(y1+y2)+m2y1y2]|y1y2|
=2m2+6+2m2-m22(m2+3)·2m2+3
=3m2+6(m2+3)2
=-3(m2+3)2+3m2+3.
因为1m2+3∈0,13,
所以实数λ的取值范围是0,23.
思路分析 (1)依题意,得直线l的方程为y=x-1,与椭圆方程联立可得2x2-3x=0.设E(x1,y1),F(x2,y2),EF中点M(x0,y0),利用根与系数的关系,中点坐标公式即可得出.
(2)设直线l的方程为x=my+1,与椭圆方程联立可得(m2+3)·y2+2my-2=0,显然m∈R.设E(x1,y1),F(x2,y2),则E1(3,y1),F1(3,y2).λ=S1S2=12(3-x1)|y1|·12(3-x2)|y2|=14[4-2m(y1+y2)+m2y1·y2]|y1y2|.利用根与系数的关系及二次函数的单调性即可得出λ的取值范围.
方法点拨 过点A(1,0)的直线斜率可能存在也可能不存在,故设方程为x=my+1,避免了分类讨论.
方法2 圆锥曲线中的定值、定点问题的解题方法
3.已知椭圆C:x2a2+y2b2=1(a>b>0)的右焦点为F(1,0),离心率为12.
(1)求椭圆C的方程;
(2)A,B是椭圆C在y轴右侧部分上的两个动点,若原点O到直线AB的距离为3,证明:△ABF的周长为定值.
解析 (1)由题意得a2=b2+1,ca=12,解得a2=4,b2=3.
所以椭圆C的方程为x24+y23=1.
(2)证明:①当直线AB垂直于x轴时,直线AB的方程为x=3,
不妨令A3,32,B3,-32,因为F(1,0),
所以|AF|=|BF|=(3-1)2+322=4-32.
因为|AB|=3,
所以|AF|+|BF|+|AB|=4.
②当直线AB不垂直于x轴时,设直线AB的方程为y=kx+m(k≠0).
因为原点O到直线AB的距离为3,
所以|m|1+k2=3,故m2=3(1+k2).
由y=kx+m,x24+y23=1,得(3+4k2)x2+8kmx+4m2-12=0,
即(3+4k2)x2+8kmx+12k2=0.
设A(x1,y1),B(x2,y2),则x1+x2=-8km3+4k2,x1x2=12k23+4k2.
所以|AB|=1+k2|x1-x2|
=1+k2(x1+x2)2-4x1x2
=1+k2·-8km3+4k22-4·12k23+4k2
=|m|3·64k2m2-48k2(3+4k2)(3+4k2)2
=4|m||k|3·33+4k2=4|m||k|3+4k2.
因为A,B在y轴右侧,所以mk<0,所以|AB|=-4mk3+4k2.
|AF|2=(x1-1)2+y12=(x1-1)2+31-x124
=14x12-2x1+4=12x1-22.
所以|AF|=2-12x1,同理,|BF|=2-12x2.
所以|AF|+|BF|=4-12(x1+x2)=4-12·-8km3+4k2=4+4km3+4k2.
所以|AF|+|BF|+|AB|=4+4km3+4k2-4km3+4k2=4.
综上,△ABF的周长为4,是定值.
4.在平面直角坐标系xOy中,动点P到点F(1,0)的距离和它到直线x=-1的距离相等,记点P的轨迹为C.
(1)求C的方程;
(2)设点A在曲线C上,x轴上一点B(在点F右侧)满足|AF|=|FB|.平行于AB的直线与曲线C相切于点D,试判断直线AD是否过定点.若过定点,求出定点的坐标;若不过定点,请说明理由.
解析 (1)因为动点P到点F(1,0)的距离和它到直线x=-1的距离相等,
所以动点P的轨迹是以点F(1,0)为焦点,直线x=-1为准线的抛物线.
设C的方程为y2=2px(p>0),则p2=1,即p=2.
所以C的方程为y2=4x.
(2)直线AD过定点.理由如下:
设Am24,m,则|AF|=m24+1=|FB|,则Bm24+2,0,
所以直线AB的斜率为m-2=-m2.
如图,设与直线AB平行,且与抛物线C相切的直线为y=-m2x+b,
由y2=4x,y=-m2x+b,得my2+8y-8b=0,
由Δ=64-4m·(-8b)=0,得b=-2m.
所以解方程是y=-4m,所以点D4m2,-4m.
当m24≠4m2,即m≠±2时,直线AD的方程为y-m=m+4mm24-4m2x-m24,
整理得y=4mm2-4(x-1),所以直线AD过点(1,0).
当m24=4m2,即m=±2时,直线AD的方程为x=1,直线AD过点(1,0).
综上所述,直线AD过定点(1,0).
方法3 存在性问题的解题策略
5.(2015四川,20,13分)如图,椭圆E:x2a2+y2b2=1(a>b>0)的离心率是22,过点P(0,1)的动直线l与椭圆相交于A,B两点.当直线l平行于x轴时,直线l被椭圆E截得的线段长为22.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得|QA||QB|=|PA||PB|恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
解析 (1)由已知得,点(2,1)在椭圆E上.
因此,2a2+1b2=1,a2-b2=c2,ca=22.解得a=2,b=2.
所以椭圆E的方程为x24+y22=1.
(2)存在.理由如下:
当直线l与x轴平行时,设直线l与椭圆相交于C,D两点.
如果存在定点Q满足条件,则有|QC||QD|=|PC||PD|=1,
即|QC|=|QD|.
所以Q点在y轴上,可设Q点的坐标为(0,y0).
当直线l与x轴垂直时,设直线l与椭圆相交于M,N两点,
则M,N的坐标分别为(0,2),(0,-2).
由|QM||QN|=|PM||PN|,有|y0-2||y0+2|=2-12+1,解得y0=1或y0=2.
所以,若存在不同于点P的定点Q满足条件,则Q点坐标只可能为(0,2).
下面证明:当Q的坐标为(0,2)时,对任意直线l,均有|QA||QB|=|PA||PB|.
当直线l的斜率不存在时,由上可知,结论成立.
当直线l的斜率存在时,可设直线l的方程为y=kx+1,A,B的坐标分别为(x1,y1),(x2,y2).
联立x24+y22=1,y=kx+1,得(2k2+1)x2+4kx-2=0.
其判别式Δ=(4k)2+8(2k2+1)>0,
所以,x1+x2=-4k2k2+1,x1x2=-22k2+1.
因此1x1+1x2=x1+x2x1x2=2k.
易知,点B关于y轴对称的点B'的坐标为(-x2,y2).
又kQA=y1-2x1=kx1-1x1=k-1x1,
kQB'=y2-2-x2=kx2-1-x2=-k+1x2=k-1x1,
所以kQA=kQB',即Q,A,B'三点共线.
所以|QA||QB|=|QA||QB'|=|x1||x2|=|PA||PB|.
故存在与P不同的定点Q(0,2),使得|QA||QB|=|PA||PB|恒成立.
过专题
【五年高考】
A组 自主命题·北京卷题组
考点一 定点与定值问题
1.(2011北京,14,5分)曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a2(a>1)的点的轨迹.给出下列三个结论:
①曲线C过坐标原点;
②曲线C关于坐标原点对称;
③若点P在曲线C上,则△F1PF2的面积不大于12a2.
其中,所有正确结论的序号是 .
答案 ②③
2.(2018北京,19,14分)已知抛物线C:y2=2px经过点P(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1)求直线l的斜率的取值范围;
(2)设O为原点,QM=λQO,QN=μQO,求证:1λ+1μ为定值.
解析 (1)因为抛物线y2=2px过点(1,2),
所以2p=4,即p=2.
故抛物线C的方程为y2=4x,
由题意知,直线l的斜率存在且不为0.
设直线l的方程为y=kx+1(k≠0).
由y2=4x,y=kx+1得k2x2+(2k-4)x+1=0.
依题意Δ=(2k-4)2-4×k2×1>0,解得k<0或0
b>0)的离心率为32,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(1)求椭圆C的方程;
(2)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN|·|BM|为定值.
解析 (1)由题意得ca=32,12ab=1,a2=b2+c2,解得a=2,b=1.
所以椭圆C的方程为x24+y2=1.
(2)证明:由(1)知,A(2,0),B(0,1).
设P(x0,y0),则x02+4y02=4.
当x0≠0时,直线PA的方程为y=y0x0-2(x-2).
令x=0,得yM=-2y0x0-2,从而|BM|=|1-yM|=1+2y0x0-2.
直线PB的方程为y=y0-1x0x+1.
令y=0,得xN=-x0y0-1,从而|AN|=|2-xN|=2+x0y0-1.
所以|AN|·|BM|=2+x0y0-1·1+2y0x0-2
=x02+4y02+4x0y0-4x0-8y0+4x0y0-x0-2y0+2
=4x0y0-4x0-8y0+8x0y0-x0-2y0+2=4.
当x0=0时,y0=-1,|BM|=2,|AN|=2,
所以|AN|·|BM|=4.
综上,|AN|·|BM|为定值.
思路分析 (1)先利用离心率和三角形的面积建立关于a,b,c的方程组,解出a,b,从而得到椭圆的方程;(2)设P(x0,y0),分x0≠0和x0=0两种情况讨论.
解后反思 条件中直线PA与y轴的交点M,直线PB与x轴的交点N是本题的突破口.解决本题的关键在于点的坐标的利用.
评析本题考查椭圆的标准方程,直线与圆锥曲线的位置关系及定值问题,方法常规,运算量大,对学生的运算能力要求较高.
考点二 参变量的取值范围与最值问题
(2011北京,19,14分)已知椭圆G:x24+y2=1.过点(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(1)求椭圆G的焦点坐标和离心率;
(2)将|AB|表示为m的函数,并求|AB|的最大值.
解析 (1)由已知得a=2,b=1,所以c=a2-b2=3.
所以椭圆G的焦点坐标为(-3,0),(3,0),离心率e=ca=32.
(2)由题意知,|m|≥1.
当m=1时,切线l的方程为x=1,点A,B的坐标分别为1,32,1,-32.此时|AB|=3.
当m=-1时,同理可得|AB|=3.
当|m|>1时,设切线l的方程为y=k(x-m).
由y=k(x-m),x24+y2=1,得(1+4k2)x2-8k2mx+4k2m2-4=0.
设A,B两点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=8k2m1+4k2,x1x2=4k2m2-41+4k2.
又由l与圆x2+y2=1相切,得|km|k2+1=1,
即m2k2=k2+1.
所以|AB|=(x2-x1)2+(y2-y1)2
=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)64k4m2(1+4k2)2-4(4k2m2-4)1+4k2=43|m|m2+3.
由于当m=±1时,|AB|=3,
所以|AB|=43|m|m2+3,m∈(-∞,-1]∪[1,+∞).
因为|AB|=43|m|m2+3=43|m|+3|m|≤2当且仅当m=±3时,|AB|=2,所以|AB|的最大值为2.
失分警示 (1)混淆椭圆的顶点与焦点、记错离心率的公式,造成失分.
(2)没有对切线的斜率是否存在进行讨论,忽视直线与圆相切的充要条件,记错直线与椭圆的相交弦长的计算公式,字母运算出错,造成失分.
评析本题考查了椭圆的基本性质,圆的切线问题,直线与椭圆的相交弦长的计算以及基本不等式的应用.考查分类讨论思想,逻辑推理能力和运算能力.解题的关键是对直线的斜率是否存在进行讨论,并能准确求出直线与椭圆的相交弦长.本题考查的知识点多、综合性强,运算量很大,属于难题.
考点三 存在性问题
(2015北京,19,14分)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为22,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线PA交x轴于点M.
(1)求椭圆C的方程,并求点M的坐标(用m,n表示);
(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.
解析 (1)由题意得b=1,ca=22,a2=b2+c2,解得a2=2.
故椭圆C的方程为x22+y2=1.设M(xM,0).
因为m≠0,所以-1b>0),四点P1(1,1),P2(0,1),P3-1,32,P41,32中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
解析 (1)由于P3,P4两点关于y轴对称,故由题设知C经过P3,P4两点.
又由1a2+1b2>1a2+34b2知,C不经过点P1,所以点P2在C上.
因此1b2=1,1a2+34b2=1,解得a2=4,b2=1.
故C的方程为x24+y2=1.
(2)证明:设直线P2A与直线P2B的斜率分别为k1,k2.
如果l与x轴垂直,设l:x=t,由题设知t≠0,且|t|<2,可得A,B的坐标分别为t,4-t22,t,-4-t22.
则k1+k2=4-t2-22t-4-t2+22t=-1,得t=2,不符合题设.
从而可设l:y=kx+m(m≠1).
将y=kx+m代入x24+y2=1得(4k2+1)x2+8kmx+4m2-4=0.
由题设可知Δ=16(4k2-m2+1)>0.
设A(x1,y1),B(x2,y2),则x1+x2=-8km4k2+1,x1x2=4m2-44k2+1.
而k1+k2=y1-1x1+y2-1x2
=kx1+m-1x1+kx2+m-1x2
=2kx1x2+(m-1)(x1+x2)x1x2,
由题设k1+k2=-1,故(2k+1)x1x2+(m-1)(x1+x2)=0.
即(2k+1)·4m2-44k2+1+(m-1)·-8km4k2+1=0.
解得k=-m+12.
当且仅当m>-1时,Δ>0,于是l:y=-m+12x+m,
即y+1=-m+12(x-2),
所以l过定点(2,-1).
方法总结 求轨迹方程的步骤:①建系、设点→②列式(列出动点所满足的几何等量关系式)→③坐标化(选用合适的公式表示几何等量关系)→④化简(注意化简前后的等价性)→⑤检验(去伪存真).
3.(2016山东文,21,14分)已知椭圆C:x2a2+y2b2=1(a>b>0)的长轴长为4,焦距为22.
(1)求椭圆C的方程;
(2)过动点M(0,m)(m>0)的直线交x轴于点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长QM交C于点B.
(i)设直线PM,QM的斜率分别为k,k',证明k'k为定值;
(ii)求直线AB的斜率的最小值.
解析 (1)设椭圆的半焦距为c.
由题意知2a=4,2c=22,
所以a=2,b=a2-c2=2.
所以椭圆C的方程为x24+y22=1.
(2)(i)证明:设P(x0,y0)(x0>0,y0>0).
由M(0,m),可得P(x0,2m),Q(x0,-2m).
所以直线PM的斜率k=2m-mx0=mx0,
直线QM的斜率k'=-2m-mx0=-3mx0.
此时k'k=-3.所以k'k为定值-3.
(ii)设A(x1,y1),B(x2,y2),直线PA的方程为y=kx+m,
直线QB的方程为y=-3kx+m.
联立y=kx+m,x24+y22=1,
整理得(2k2+1)x2+4mkx+2m2-4=0.
由x0x1=2m2-42k2+1,可得x1=2(m2-2)(2k2+1)x0.
所以y1=kx1+m=2k(m2-2)(2k2+1)x0+m.
同理x2=2(m2-2)(18k2+1)x0,y2=-6k(m2-2)(18k2+1)x0+m.
所以x2-x1=2(m2-2)(18k2+1)x0-2(m2-2)(2k2+1)x0=-32k2(m2-2)(18k2+1)(2k2+1)x0,
y2-y1=-6k(m2-2)(18k2+1)x0+m-2k(m2-2)(2k2+1)x0-m=-8k(6k2+1)(m2-2)(18k2+1)(2k2+1)x0,
所以kAB=y2-y1x2-x1=6k2+14k=146k+1k.
由m>0,x0>0,可知k>0,
所以6k+1k≥26,等号当且仅当k=66时取得.
此时m4-8m2=66,即m=147,符合题意.
所以直线AB的斜率的最小值为62.
4.(2015课标Ⅱ文,20,12分)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为22,点(2,2)在C上.
(1)求C的方程;
(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.
解析 (1)由题意有a2-b2a=22,4a2+2b2=1,
解得a2=8,b2=4.
所以C的方程为x28+y24=1.
(2)证明:设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).将y=kx+b代入x28+y24=1得
(2k2+1)x2+4kbx+2b2-8=0.
故xM=x1+x22=-2kb2k2+1,yM=k·xM+b=b2k2+1.
于是直线OM的斜率kOM=yMxM=-12k,即kOM·k=-12.
所以直线OM的斜率与直线l的斜率的乘积为定值.
考点二 参变量的取值范围与最值问题
1.(2018浙江,17,4分)已知点P(0,1),椭圆x24+y2=m(m>1)上两点A,B满足AP=2PB,则当m= 时,点B横坐标的绝对值最大.
答案 5
2.(2018浙江,21,15分)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+y24=1(x<0)上的动点,求△PAB面积的取值范围.
解析 本题主要考查椭圆、抛物线的几何性质,直线与抛物线的位置关系等基础知识,同时考查运算求解能力和综合应用能力.
(1)证明:设P(x0,y0),A14y12,y1,B14y22,y2.
因为PA,PB的中点在抛物线上,
所以y1,y2为方程y+y022=4·14y2+x02,
即y2-2y0y+8x0-y02=0的两个不同的实根.
所以y1+y2=2y0,
因此,PM垂直于y轴.
(2)由(1)可知y1+y2=2y0,y1y2=8x0-y02,
所以|PM|=18(y12+y22)-x0=34y02-3x0,
|y1-y2|=22(y02-4x0).
因此,△PAB的面积S△PAB=12|PM|·|y1-y2|=324(y02-4x0)32.
因为x02+y024=1(x0<0),所以y02-4x0=-4x02-4x0+4∈[4,5].
因此,△PAB面积的取值范围是62,15104.
疑难突破 解析几何中“取值范围”与“最值”问题
在解析几何中,求某个量(直线斜率,直线在x、y轴上的截距,弦长,三角形或四边形面积等)的取值范围或最值问题的关键是利用条件把所求量表示成关于某个变量(通常是直线斜率,动点的横、纵坐标等)的函数,并求出这个变量的取值范围(即函数的定义域),将问题转化为求函数的值域或最值.
3.(2016课标Ⅰ,20,12分)设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
解析 (1)证明:因为|AD|=|AC|,EB∥AC,
故∠EBD=∠ACD=∠ADC.
所以|EB|=|ED|,
故|EA|+|EB|=|EA|+|ED|=|AD|.
又圆A的标准方程为(x+1)2+y2=16,
从而|AD|=4,所以|EA|+|EB|=4.
由题设得A(-1,0),B(1,0),|AB|=2,
由椭圆定义可得点E的轨迹方程为x24+y23=1(y≠0).
(2)当l与x轴不垂直时,设l的方程为y=k(x-1)(k≠0),
M(x1,y1),N(x2,y2).
由y=k(x-1),x24+y23=1得(4k2+3)x2-8k2x+4k2-12=0.
则x1+x2=8k24k2+3,x1x2=4k2-124k2+3.
所以|MN|=1+k2|x1-x2|=12(k2+1)4k2+3.
过点B(1,0)且与l垂直的直线m:y=-1k(x-1),A到m的距离为2k2+1,
所以|PQ|=242-2k2+12=44k2+3k2+1.
故四边形MPNQ的面积S=12|MN|·|PQ|=121+14k2+3.
可得当l与x轴不垂直时,四边形MPNQ面积的取值范围为(12,83).
当l与x轴垂直时,其方程为x=1,|MN|=3,|PQ|=8,四边形MPNQ的面积为12.
综上,四边形MPNQ面积的取值范围为[12,83).
方法总结 定义法求轨迹方程的一般步骤:
(1)判定动点的运动轨迹满足某种曲线的定义;
(2)设标准方程,求方程中的基本量;
(3)写出轨迹方程.
4.(2015山东,20,13分)平面直角坐标系xOy中,已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为32,左、右焦点分别是F1,F2.以F1为圆心以3为半径的圆与以F2为圆心以1为半径的圆相交,且交点在椭圆C上.
(1)求椭圆C的方程;
(2)设椭圆E:x24a2+y24b2=1,P为椭圆C上任意一点.过点P的直线y=kx+m交椭圆E于A,B两点,射线PO交椭圆E于点Q.
(i)求|OQ||OP|的值;
(ii)求△ABQ面积的最大值.
解析 (1)由题意知2a=4,则a=2.
又ca=32,a2-c2=b2,可得b=1,
所以椭圆C的方程为x24+y2=1.
(2)由(1)知椭圆E的方程为x216+y24=1.
(i)设P(x0,y0),|OQ||OP|=λ,由题意知Q(-λx0,-λy0).
因为x024+y02=1,
又(-λx0)216+(-λy0)24=1,
即λ24x024+y02=1,
所以λ=2,即|OQ||OP|=2.
(ii)设A(x1,y1),B(x2,y2).
将y=kx+m代入椭圆E的方程,
可得(1+4k2)x2+8kmx+4m2-16=0,
由Δ>0,可得m2<4+16k2.①
由根与系数的关系得x1+x2=-8km1+4k2,x1x2=4m2-161+4k2.
所以|x1-x2|=416k2+4-m21+4k2.
因为直线y=kx+m与y轴交点的坐标为(0,m),
所以△OAB的面积S=12|m||x1-x2|
=216k2+4-m2|m|1+4k2
=2(16k2+4-m2)m21+4k2
=24-m21+4k2m21+4k2.
设m21+4k2=t.
将y=kx+m代入椭圆C的方程,
可得(1+4k2)x2+8kmx+4m2-4=0,
由Δ≥0,可得m2≤1+4k2.②
由①②可知00,b1>0)和椭圆C2:y2a22+x2b22=1(a2>b2>0)均过点P233,1,且以C1的两个顶点和C2的两个焦点为顶点的四边形是面积为2的正方形.
(1)求C1,C2的方程;
(2)是否存在直线l,使得l与C1交于A,B两点,与C2只有一个公共点,且|OA+OB|=|AB|?证明你的结论.
解析 (1)设C2的焦距为2c2,由题意知,2c2=2,2a1=2,
从而a1=1,c2=1.
因为点P233,1在双曲线x2-y2b12=1上,所以2332-1b12=1,故b12=3.
由椭圆的定义知2a2=2332+(1-1)2+2332+(1+1)2=23.
于是a2=3,b22=a22-c22=2,故C1,C2的方程分别为x2-y23=1,y23+x22=1.
(2)不存在符合题设条件的直线.证明如下:
(i)若直线l垂直于x轴,因为l与C2只有一个公共点,所以直线l的方程为x=2或x=-2.
当x=2时,易知A(2,3),B(2,-3),
所以|OA+OB|=22,|AB|=23,
此时,|OA+OB|≠|AB|.
当x=-2时,同理可知,|OA+OB|≠|AB|.
(ii)若直线l不垂直于x轴,设l的方程为y=kx+m,
由y=kx+m,x2-y23=1得(3-k2)x2-2kmx-m2-3=0.
当l与C1相交于A,B两点时,设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,从而x1+x2=2km3-k2,x1x2=m2+3k2-3.
于是y1y2=k2x1x2+km(x1+x2)+m2=3k2-3m2k2-3.
由y=kx+m,y23+x22=1得(2k2+3)x2+4kmx+2m2-6=0.
因为直线l与C2只有一个公共点,所以上述方程的判别式
Δ=16k2m2-8(2k2+3)(m2-3)=0.
化简,得2k2=m2-3,因此OA·OB=x1x2+y1y2=m2+3k2-3+3k2-3m2k2-3=-k2-3k2-3≠0,
于是OA2+OB2+2OA·OB≠OA2+OB2-2OA·OB,
即|OA+OB|2≠|OA-OB|2,
故|OA+OB|≠|AB|.
综合(i),(ii)可知,不存在符合题设条件的直线.
评析本题考查椭圆与双曲线的定义、几何性质、标准方程及直线与圆锥曲线的位置关系,同时考查方程思想,运算、推理能力,综合性较强.
2.(2014山东文,21,14分)在平面直角坐标系xOy中,椭圆C:x2a2+y2b2=1(a>b>0)的离心率为32,直线y=x被椭圆C截得的线段长为4105.
(1)求椭圆C的方程;
(2)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.
(i)设直线BD,AM的斜率分别为k1,k2.证明存在常数λ使得k1=λk2,并求出λ的值;
(ii)求△OMN面积的最大值.
解析 (1)由题意知a2-b2a=32,可得a2=4b2,
椭圆C的方程可简化为x2+4y2=a2.
将y=x代入可得x=±5a5,
因此2×25a5=4105,可得a=2.
因此b=1,
所以椭圆C的方程为x24+y2=1.
(2)(i)证明:设A(x1,y1)(x1y1≠0),D(x2,y2),
则B(-x1,-y1),
因为直线AB的斜率kAB=y1x1,
又AB⊥AD,所以直线AD的斜率k=-x1y1.
设直线AD的方程为y=kx+m,由题意知k≠0,m≠0.
由y=kx+m,x24+y2=1可得(1+4k2)x2+8mkx+4m2-4=0.
所以x1+x2=-8mk1+4k2,
因此y1+y2=k(x1+x2)+2m=2m1+4k2.
由题意知x1≠-x2,所以k1=y1+y2x1+x2=-14k=y14x1.
所以直线BD的方程为y+y1=y14x1(x+x1).
令y=0,得x=3x1,即M(3x1,0).
可得k2=-y12x1.所以k1=-12k2,即λ=-12.
因此存在常数λ=-12使得结论成立.
(ii)直线BD的方程为y+y1=y14x1(x+x1),
令x=0,得y=-34y1,即N0,-34y1.
由(i)知M(3x1,0),
可得△OMN的面积S=12×3|x1|×34|y1|=98|x1||y1|.
因为|x1||y1|≤x124+y12=1,当且仅当|x1|2=|y1|=22时等号成立,
此时S取得最大值98,
所以△OMN面积的最大值为98.
C组 教师专用题组
考点一 定点与定值问题
1.(2014江西,20,13分)如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
(1)证明:动点D在定直线上;
(2)作C的任意一条切线l(不含x轴),与直线y=2相交于点N1,与(1)中的定直线相交于点N2.证明:|MN2|2-|MN1|2为定值,并求此定值.
解析 (1)证明:依题意可设直线AB的方程为y=kx+2,代入x2=4y,得x2=4(kx+2),即x2-4kx-8=0.
设A(x1,y1),B(x2,y2),则有x1x2=-8,
直线AO的方程为y=y1x1x,直线BD的方程为x=x2.
解得交点D的坐标为x2,y1x2x1,
注意到x1x2=-8及x12=4y1,则有y=y1x1x2x12=-8y14y1=-2.
因此D点在定直线y=-2上(x≠0).
(2)依题设知,切线l的斜率存在且不等于0,设切线l的方程为y=ax+b(a≠0),代入x2=4y得x2=4(ax+b),即x2-4ax-4b=0,由Δ=0得(4a)2+16b=0,化简整理得b=-a2.
故切线l的方程可写为y=ax-a2.
分别令y=2、y=-2得N1、N2的坐标为
N12a+a,2、N2-2a+a,-2,
则|MN2|2-|MN1|2=2a-a2+42-2a+a2=8,
即|MN2|2-|MN1|2为定值8.
评析本题考查抛物线的性质,以及直线与抛物线的位置关系,考查用代数方法解决圆锥曲线的综合问题,考查方程思想以及设而不求、整体代换思想的应用,同时考查学生运算求解能力和综合分析问题的能力.
2.(2013陕西,20,13分)已知动圆过定点A(4,0),且在y轴上截得弦MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
解析 (1)如图,设动圆圆心为O1(x,y),由题意,知|O1A|=|O1M|,当O1不在y轴上时,过O1作O1H⊥MN交MN于H,则H是MN的中点,
∴|O1M|=x2+42,
又|O1A|=(x-4)2+y2,∴(x-4)2+y2=x2+42,
化简得y2=8x(x≠0).
又当O1在y轴上时,O1与O重合,点O1的坐标(0,0)也满足方程y2=8x,∴动圆圆心的轨迹C的方程为y2=8x.
(2)由题意,设直线l的方程为y=kx+b(k≠0),P(x1,y1),Q(x2,y2),
将y=kx+b代入y2=8x中,
得k2x2+(2bk-8)x+b2=0.
其中Δ=-32kb+64>0.
由根与系数的关系得,x1+x2=8-2bkk2,①
x1x2=b2k2,②
∵x轴平分∠PBQ,∴y1x1+1=-y2x2+1,
即y1(x2+1)+y2(x1+1)=0,
(kx1+b)(x2+1)+(kx2+b)(x1+1)=0,
2kx1x2+(b+k)(x1+x2)+2b=0,③
将①,②代入③得2kb2+(k+b)(8-2bk)+2k2b=0,
∴k=-b,此时Δ>0,
∴直线l的方程为y=k(x-1),即直线l过定点(1,0).
3.(2013江西,20,13分)椭圆C:x2a2+y2b2=1(a>b>0)的离心率e=32,a+b=3.
(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明:2m-k为定值.
解析 (1)因为e=32=ca,
所以a=23c,b=13c.代入a+b=3得,c=3,a=2,b=1.
故椭圆C的方程为x24+y2=1.
(2)证明:证法一:因为B(2,0),P不为椭圆顶点,则直线BP的方程为y=k(x-2)k≠0,k≠±12,①
将①代入x24+y2=1,
解得P8k2-24k2+1,-4k4k2+1.
直线AD的方程为y=12x+1.②
①与②联立解得M4k+22k-1,4k2k-1.
由D(0,1),P8k2-24k2+1,-4k4k2+1,N(x,0)三点共线知-4k4k2+1-18k2-24k2+1-0=0-1x-0,解得N4k-22k+1,0.
所以MN的斜率为m=4k2k-1-04k+22k-1-4k-22k+1
=4k(2k+1)2(2k+1)2-2(2k-1)2=2k+14,
则2m-k=2k+12-k=12(定值).
证法二:设P(x0,y0)(x0≠0,±2),则k=y0x0-2,
直线AD的方程为y=12(x+2),
直线BP的方程为y=y0x0-2(x-2),
直线DP的方程为y-1=y0-1x0x,
令y=0,由y0≠1可得N-x0y0-1,0,
由y=12(x+2),y=y0x0-2(x-2),
解得M4y0+2x0-42y0-x0+2,4y02y0-x0+2,因此MN的斜率为
m=4y02y0-x0+24y0+2x0-42y0-x0+2+x0y0-1
=4y0(y0-1)4y02-8y0+4x0y0-x02+4
=4y0(y0-1)4y02-8y0+4x0y0-(4-4y02)+4
=y0-12y0+x0-2,
所以2m-k=2(y0-1)2y0+x0-2-y0x0-2
=2(y0-1)(x0-2)-y0(2y0+x0-2)(2y0+x0-2)(x0-2)
=2(y0-1)(x0-2)-2y02-y0(x0-2)(2y0+x0-2)(x0-2)
=2(y0-1)(x0-2)-12(4-x02)-y0(x0-2)(2y0+x0-2)(x0-2)
=12(定值).
评析本题考查了直线和椭圆的位置关系,考查了定值问题,考查了运算求解能力和数据处理能力.
4.(2014安徽,19,13分)如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.
(1)证明:A1B1∥A2B2;
(2)过O作直线l(异于l1,l2)与E1,E2分别交于C1,C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2,求S1S2的值.
解析 (1)证明:设直线l1,l2的方程分别为y=k1x,y=k2x(k1,k2≠0),则
由y=k1x,y2=2p1x,得A12p1k12,2p1k1,
由y=k1x,y2=2p2x,得A22p2k12,2p2k1.
同理可得B12p1k22,2p1k2,B22p2k22,2p2k2.
所以A1B1=2p1k22-2p1k12,2p1k2-2p1k1=2p11k22-1k12,1k2-1k1,
A2B2=2p2k22-2p2k12,2p2k2-2p2k1=2p21k22-1k12,1k2-1k1,
故A1B1=p1p2A2B2,所以A1B1∥A2B2.
(2)由(1)知A1B1∥A2B2,同理可得B1C1∥B2C2,C1A1∥C2A2.
所以△A1B1C1∽△A2B2C2.
因此S1S2=|A1B1||A2B2|2.
又由(1)中的A1B1=p1p2A2B2知|A1B1||A2B2|=p1p2.
故S1S2=p12p22.
考点二 参变量的取值范围与最值问题
1.(2014湖北,9,5分)已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=π3,则椭圆和双曲线的离心率的倒数之和的最大值为( )
A.433 B.233 C.3 D.2
答案 A
2.(2014四川,10,5分)已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA·OB=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2 B.3 C.1728 D.10
答案 B
3.(2017山东文,21,14分)在平面直角坐标系xOy中,已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为22,椭圆C截直线y=1所得线段的长度为22.
(1)求椭圆C的方程;
(2)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,☉N的半径为|NO|.设D为AB的中点,DE,DF与☉N分别相切于点E,F,求∠EDF的最小值.
解析 (1)由椭圆的离心率为22,得a2=2(a2-b2),
又当y=1时,x2=a2-a2b2,得a2-a2b2=2,
所以a2=4,b2=2.
因此椭圆方程为x24+y22=1.
(2)设A(x1,y1),B(x2,y2),联立方程y=kx+m,x2+2y2=4,
得(2k2+1)x2+4kmx+2m2-4=0,
由Δ>0得m2<4k2+2,(*)
且x1+x2=-4km2k2+1,因此y1+y2=2m2k2+1,
所以D-2km2k2+1,m2k2+1,
又N(0,-m),所以|ND|2=-2km2k2+12+m2k2+1+m2,
整理得|ND|2=4m2(1+3k2+k4)(2k2+1)2,
因为|NF|=|m|,
所以|ND|2|NF|2=4(k4+3k2+1)(2k2+1)2=1+8k2+3(2k2+1)2.
令t=8k2+3,t≥3,故2k2+1=t+14,
所以|ND|2|NF|2=1+16t(1+t)2=1+16t+1t+2.
令y=t+1t,所以y'=1-1t2.
当t≥3时,y'>0,
从而y=t+1t在[3,+∞)上单调递增,
因此t+1t≥103,
等号当且仅当t=3时成立,此时k=0,
所以|ND|2|NF|2≤1+3=4,
由(*)得-20),则p2=1,所以抛物线C的方程为x2=4y.
(2)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1.
由y=kx+1,x2=4y消去y,整理得x2-4kx-4=0,
所以x1+x2=4k,x1x2=-4.
从而|x1-x2|=4k2+1.
由y=y1x1x,y=x-2,
解得点M的横坐标xM=2x1x1-y1=2x1x1-x124=84-x1.
同理点N的横坐标xN=84-x2.
所以|MN|=2|xM-xN|
=284-x1-84-x2
=82x1-x2x1x2-4(x1+x2)+16
=82k2+1|4k-3|.
令4k-3=t,t≠0,则k=t+34.
当t>0时,|MN|=2225t2+6t+1>22.
当t<0时,|MN|=225t+352+1625≥85 2.
综上所述,当t=-253,即k=-43时,
|MN|的最小值是85 2.
评析本题主要考查抛物线的几何性质、直线与抛物线的位置关系,同时考查解析几何的基本思想方法和运算求解能力.
考点三 存在性问题
1.(2015课标Ⅱ,20,12分)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)若l过点m3,m,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
解析 (1)证明:设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).
将y=kx+b代入9x2+y2=m2得(k2+9)x2+2kbx+b2-m2=0,故
xM=x1+x22=-kbk2+9,yM=kxM+b=9bk2+9.
于是直线OM的斜率kOM=yMxM=-9k,即kOM·k=-9.
所以直线OM的斜率与l的斜率的乘积为定值.
(2)四边形OAPB能为平行四边形.
因为直线l过点m3,m,所以l不过原点且与C有两个交点的充要条件是k>0,k≠3.
由(1)得OM的方程为y=-9kx.
设点P的横坐标为xP.
由y=-9kx,9x2+y2=m2得xP2=k2m29k2+81,即xP=±km3k2+9.
将m3,m代入l的方程得b=m(3-k)3,
因此xM=k(k-3)m3(k2+9).
四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分,即xP=2xM.
于是±km3k2+9=2×k(k-3)m3(k2+9),
解得k1=4-7,k2=4+7.
因为ki>0,ki≠3,i=1,2,
所以当l的斜率为4-7或4+7时,四边形OAPB为平行四边形.
评析本题考查直线与圆锥曲线的位置关系,设问常规,但对运算能力要求较高,考查学生的思维能力.
2.(2014重庆文,21,12分)如图,设椭圆x2a2+y2b2=1(a>b>0)的左,右焦点分别为F1,F2,点D在椭圆上,DF1⊥F1F2,|F1F2||DF1|=22,△DF1F2的面积为22.
(1)求该椭圆的标准方程;
(2)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求出圆的方程.若不存在,请说明理由.
解析 (1)设F1(-c,0),F2(c,0),其中c2=a2-b2.
由|F1F2||DF1|=22得|DF1|=|F1F2|22=22c.
从而S△DF1F2=12|DF1||F1F2|=22c2=22,故c=1.
从而|DF1|=22,
由DF1⊥F1F2得|DF2|2=|DF1|2+|F1F2|2=92,
因此|DF2|=322.
所以2a=|DF1|+|DF2|=22,故a=2,b2=a2-c2=1.
因此,所求椭圆的标准方程为x22+y2=1.
(2)如图,设圆心在y轴上的圆C与椭圆x22+y2=1相交,P1(x1,y1),P2(x2,y2)是两个交点,y1>0,y2>0,F1P1,F2P2是圆C的切线,且F1P1⊥F2P2.
由圆和椭圆的对称性,易知,x2=-x1,y1=y2.
由(1)知F1(-1,0),F2(1,0),所以F1P1=(x1+1,y1),F2P2=(-x1-1,y1).
再由F1P1⊥F2P2得-(x1+1)2+y12=0.
由椭圆方程得1-x122=(x1+1)2,
即3x12+4x1=0,
解得x1=-43或x1=0.
当x1=0时,P1,P2重合,不存在满足题设要求的圆.
当x1=-43时,过P1,P2分别与F1P1,F2P2垂直的直线的交点即为圆心C.
设C(0,y0),由CP1⊥F1P1,得y1-y0x1·y1x1+1=-1.
而y1=1-x122=13,故y0=53.
圆C的半径|CP1|=-432+13-532=423.
综上,存在满足题设条件的圆,其方程为x2+y-532=329.
评析本题考查椭圆的标准方程、圆的方程的求法以及椭圆的几何性质、直线与圆的位置关系的应用.本题考查了学生分析问题,解决问题的能力、逻辑推理能力、运算求解能力以及利用分类讨论思想解决问题的能力.
3.(2013安徽,21,13分)已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为4,且过点P(2,3).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,22),连接AE.过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG.问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
解析 (1)因为焦距为4,所以a2-b2=4.又因为椭圆C过点P(2,3),所以2a2+3b2=1,故a2=8,b2=4,从而椭圆C的方程为x28+y24=1.
(2)由题意知,E点坐标为(x0,0),设D(xD,0),则AE=(x0,-22),AD=(xD,-22),
再由AD⊥AE知,AE·AD=0,
即x0xD+8=0.
由于x0y0≠0,故xD=-8x0.
因为点G是点D关于y轴的对称点,所以点G8x0,0.
故直线QG的斜率kQG=y0x0-8x0=x0y0x02-8.
又因Q(x0,y0)在椭圆C上,
所以x02+2y02=8.①
从而kQG=-x02y0.
故直线QG的方程为
y=-x02y0x-8x0.②
将②代入椭圆C的方程,得
(x02+2y02)x2-16x0x+64-16y02=0.③
再将①代入③,化简得
x2-2x0x+x02=0.
解得x=x0,y=y0,即直线QG与椭圆C一定有唯一的公共点.
评析本题考查椭圆的标准方程及其几何性质,直线与椭圆的位置关系.考查了数形结合思想、逻辑推理能力及运算求解能力.
4.(2013湖北,22,14分)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D.记λ=mn,△BDM和△ABN的面积分别为S1和S2.
(1)当直线l与y轴重合时,若S1=λS2,求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.
解析 依题意可设椭圆C1和C2的方程分别为C1:x2a2+y2m2=1,C2:x2a2+y2n2=1.其中a>m>n>0,λ=mn>1.
(1)解法一:如图1,若直线l与y轴重合,即直线l的方程为x=0,则S1=12|BD|·|OM|=12a|BD|,
S2=12|AB|·|ON|=12a|AB|,所以S1S2=|BD||AB|.
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
所以|BD||AB|=|yB-yD||yA-yB|=m+nm-n=λ+1λ-1.
若S1S2=λ,即λ+1λ-1=λ,化简得λ2-2λ-1=0.
由λ>1,解得λ=2+1.
故当直线l与y轴重合时,若S1=λS2,则λ=2+1.
解法二:如图1,若直线l与y轴重合,则|BD|=|OB|+|OD|=m+n,|AB|=|OA|-|OB|=m-n;
S1=12|BD|·|OM|=12a|BD|,
S2=12|AB|·|ON|=12a|AB|.
所以S1S2=|BD||AB|=m+nm-n=λ+1λ-1.
若S1S2=λ,即λ+1λ-1=λ,化简得λ2-2λ-1=0.
由λ>1,解得λ=2+1.
故当直线l与y轴重合时,若S1=λS2,则λ=2+1.
(2)解法一:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2.
因为d1=|-ak-0|1+k2=ak1+k2,d2=|ak-0|1+k2=ak1+k2,
所以d1=d2.
又因为S1=12|BD|d1,S2=12|AB|d2,所以S1S2=|BD||AB|=λ,
即|BD|=λ|AB|.
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,|AD|=|BD|+|AB|=(λ+1)|AB|,
所以|AD||BC|=λ+1λ-1.①
将l的方程分别与C1,C2的方程联立,
可求得xA=ama2k2+m2,xB=ana2k2+n2.
根据对称性可知xC=-xB,xD=-xA,
所以|AD||BC|=1+k2|xA-xD|1+k2|xB-xC|=2xA2xB=mna2k2+n2a2k2+m2.②
从而由①②可得a2k2+n2a2k2+m2=λ+1λ(λ-1).③
令t=λ+1λ(λ-1),则由m>n,可得t≠1,
所以由③解得k2=n2(λ2t2-1)a2(1-t2).
因为k≠0,所以k2>0.所以③式关于k有解,当且仅当n2(λ2t2-1)a2(1-t2)>0,等价于(t2-1)t2-1λ2<0.由λ>1,解得1λ1,解得λ>1+2,所以
当1<λ≤1+2时,不存在与坐标轴不重合的直线l,使得S1=λS2;
当λ>1+2时,存在与坐标轴不重合的直线l,使得S1=λS2.
解法二:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,
因为d1=|-ak-0|1+k2=ak1+k2,d2=|ak-0|1+k2=ak1+k2,所以d1=d2.
又S1=12|BD|d1,S2=12|AB|d2,所以S1S2=|BD||AB|=λ.
因为|BD||AB|=1+k2|xB-xD|1+k2|xA-xB|=xA+xBxA-xB=λ,所以xAxB=λ+1λ-1.
由点A(xA,kxA),B(xB,kxB)分别在C1,C2上,可得
xA2a2+k2xA2m2=1,xB2a2+k2xB2n2=1,两式相减可得xA2-xB2a2+k2(xA2-λ2xB2)m2=0,依题意xA>xB>0,所以xA2>xB2.所以由上式解得k2=m2(xA2-xB2)a2(λ2xB2-xA2).
因为k2>0,所以由m2(xA2-xB2)a2(λ2xB2-xA2)>0,
解得11+2,所以
当1<λ≤1+2时,不存在与坐标轴不重合的直线l,使得S1=λS2;
当λ>1+2时,存在与坐标轴不重合的直线l,使得S1=λS2.
5.(2014山东,21,14分)已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|.当点A的横坐标为3时,△ADF为正三角形.
(1)求C的方程;
(2)若直线l1∥l,且l1和C有且只有一个公共点E,
(i)证明直线AE过定点,并求出定点坐标;
(ii)△ABE的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
解析 (1)由题意知Fp2,0.
设D(t,0)(t>0),则FD的中点为p+2t4,0.
因为|FA|=|FD|,
由抛物线的定义知3+p2=t-p2,
解得t=3+p或t=-3(舍去).
由p+2t4=3,解得p=2.
所以抛物线C的方程为y2=4x.
(2)(i)由(1)知F(1,0),
设A(x0,y0)(x0y0≠0),D(xD,0)(xD>0),
因为|FA|=|FD|,则|xD-1|=x0+1,
由xD>0得xD=x0+2,故D(x0+2,0).
故直线AB的斜率kAB=-y02.
因为直线l1和直线AB平行,
所以设直线l1的方程为y=-y02x+b,
代入抛物线方程得y2+8y0y-8by0=0,
由题意得Δ=64y02+32by0=0,得b=-2y0.
设E(xE,yE),则yE=-4y0,xE=4y02,
当y02≠4时,kAE=yE-y0xE-x0=-4y0+y04y02-y024=4y0y02-4,
可得直线AE的方程为y-y0=4y0y02-4(x-x0),
由y02=4x0,
整理可得y=4y0y02-4(x-1),
直线AE恒过点F(1,0).
当y02=4时,直线AE的方程为x=1,过点F(1,0),
所以直线AE过定点F(1,0).
(ii)由(i)知直线AE过焦点F(1,0),
所以|AE|=|AF|+|FE|=(x0+1)+1x0+1=x0+1x0+2.
设直线AE的方程为x=my+1,
因为点A(x0,y0)在直线AE上,
故m=x0-1y0,
设B(x1,y1),
直线AB的方程为y-y0=-y02(x-x0),
由于y0≠0,
可得x=-2y0y+2+x0,
代入抛物线方程得y2+8y0y-8-4x0=0.
所以y0+y1=-8y0,
可求得y1=-y0-8y0,x1=4x0+x0+4,
所以点B到直线AE的距离为
d=4x0+x0+4+my0+8y0-11+m2
=4(x0+1)x0
=4x0+1x0.
则△ABE的面积S=12×4x0+1x0x0+1x0+2≥16,
当且仅当1x0=x0,即x0=1时等号成立.
所以△ABE的面积的最小值为16.
评析本题考查抛物线的标准方程、几何性质、直线与圆锥曲线的位置关系以及解析几何中的定点问题、最值问题和结论探究性问题.本题综合性较强、难度较大,很好地考查了考生的逻辑思维能力和运算求解能力.本题的易错点是定点的确定.
【三年模拟】
一、填空题(每小题5分,共15分)
1.(2017北京朝阳一模,14)在平面直角坐标系xOy中,动点P(x,y)到两坐标轴的距离之和等于它到定点(1,1)的距离,记点P的轨迹为C.给出下面四个结论:
①曲线C关于原点对称;
②曲线C关于直线y=x对称;
③点(-a2,1)(a∈R)在曲线C上;
④在第一象限内,曲线C与x轴的非负半轴、y轴的非负半轴围成的封闭图形的面积小于12.
其中所有正确结论的序号是 .
答案 ②③④
2.(2017北京海淀二模,14)已知椭圆G:x26+y2b2=1(0b>0)的离心率等于22,经过其左焦点F(-1,0)且与x轴不重合的直线l与椭圆C交于M,N两点.
(1)求椭圆C的方程;
(2)O为原点,在x轴上是否存在定点Q,使得点F到直线QM,QN的距离总相等?若存在,求出点Q的坐标;若不存在,请说明理由.
解析 (1)由题意得1a=22,a2=b2+1,解得a=2,b=1.
故椭圆C的方程为x22+y2=1.
(2)存在.当直线MN的斜率存在时,设直线MN的方程为y=k(x+1)(k≠0).
由y=k(x+1),x22+y2=1得(1+2k2)x2+4k2x+2k2-2=0.
易得Δ>0.设M(x1,y1),N(x2,y2),
则x1+x2=-4k21+2k2,①x1x2=2k2-21+2k2.②
设Q(t,0).由于点M,N在x轴异侧,则问题等价于“QF平分∠MQN”,且x1≠t,x2≠t,即等价于“kQM+kQN=y1x1-t+y2x2-t=0”,即y1(x2-t)+y2(x1-t)=0.
将y1=k(x1+1),y2=k(x2+1)代入上式,
整理得2x1x2+(x1+x2)(1-t)-2t=0.
将①②代入上式,整理得t+2=0,即t=-2,所以Q(-2,0).
当直线MN的斜率不存在时,存在Q(-2,0)也使得点F到直线QM,QN的距离相等.
故在x轴上存在定点Q(-2,0),使得点F到直线QM,QN的距离总相等.
5.(2018北京房山二模文,19)椭圆C:x2a2+y2b2=1(a>b>0)的离心率为12,O为坐标原点,F是椭圆C的右焦点,A为椭圆C上一点,且AF⊥x轴,△AFO的面积为34.
(1)求椭圆C的方程;
(2)过C上一点P(x0,y0)(y0≠0)的直线l:x0xa2+y0yb2=1与直线AF相交于点M,与直线x=4相交于点N.证明:当点P在C上移动时,|MF||NF|恒为定值,并求出此定值.
解析 (1)设F(c,0),A(c,d),则c2a2+d2b2=1,
∵ca=12,∴|d|=32b.∵△AFO的面积为34,
∴12c|d|=12c·32b=34,∴bc=3.
由a2-b2=c2,a=2c,bc=3,得a=2,b=3,c=1.
故椭圆C的方程为x24+y23=1.
(2)结合(1)知直线l的方程为x0x4+y0y3=1(y0≠0),
则y=12-3x0x4y0(y0≠0).
∴直线l与直线AF的交点坐标为M1,12-3x04y0,
直线l与直线x=4的交点坐标为N4,3-3x0y0,
则|MF|2|NF|2=12-3x04y029+3-3x0y02=(4-x0)216y02+16(1-x0)2,(*)
∵P(x0,y0)是椭圆C上一点,
∴x024+y023=1,则y02=3-3x024,
代入(*)式得,
|MF|2|NF|2=(4-x0)248-12x02+16-32x0+16x02=(4-x0)24(x02-8x0+16)
=14·(4-x0)2(4-x0)2=14,
故|MF||NF|=12,恒为定值.
6.(2018北京海淀二模文,20)已知椭圆C:x2+2y2=2的左、右顶点分别为A1、A2.
(1)求椭圆C的长轴长与离心率;
(2)若不垂直于x轴的直线l与椭圆C相交于P,Q两点,直线A1P与A2Q交于点M,直线A1Q与A2P交于点N.求证:直线MN垂直于x轴.
解析 (1)椭圆C的方程可化为x22+y2=1,
所以a=2,b=1,c=1.
所以长轴长为2a=22,离心率e=ca=22.
(2)证明:显然直线A1P、A2Q、A1Q、A2P斜率都存在,且互不相等,分别设为k1,k2,k3,k4.
则直线A1P的方程为y=k1(x+2),A2Q的方程为y=k2(x-2),
联立y=k1(x+2),y=k2(x-2),可得xM=2(k2+k1)k2-k1.
同理可得xN=2(k4+k3)k4-k3.
设P(x0,y0),则x02+2y02=2.
所以k1k4=y0x0+2·y0x0-2=y02x02-2=y02-2y02=-12.
同理,k2k3=-12.
所以xN=2-12k1+-12k2-12k1--12k2=2(k2+k1)k2-k1=xM.
所以直线MN垂直于x轴.
7.(2019届北京大兴9月统练,18)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为32,长轴的一个顶点为A,短轴的一个顶点为B,O为坐标原点,且S△OAB=5.
(1)求椭圆C的标准方程;
(2)直线l:y=x+m与椭圆C交于P,Q两点,且直线l不经过点M(4,1).记直线MP,MQ的斜率分别为k1,k2,问:k1+k2是不是定值?并说明理由.
解析 (1)由题意知,12ab=5,a2-b2=c2,ca=32,解得a2=20,b2=5,c2=15,
故椭圆C的标准方程为x220+y25=1.
(2)k1+k2=0,理由如下:
设P(x1,y1),Q(x2,y2),
联立得y=x+m,x220+y25=1,得5x2+8mx+4m2-20=0,
由Δ=(8m)2-20(4m2-20)>0,解得-5b>0)的上、下顶点分别为A,B,且AB=2,离心率为32,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设P,Q是椭圆C上的两个动点(不与A,B重合),且关于y轴对称,M,N分别是OP,BP的中点,直线AM与椭圆C的另一个交点为D.求证:D,N,Q三点共线.
解析 (1)因为椭圆的焦点在x轴上,AB=2,离心率e=32,所以b=1,ca=32.又由a2=b2+c2,得a2=4.
所以椭圆C的标准方程是x24+y2=1.
(2)证明:设点P的坐标为(x0,y0),
所以点Q的坐标为(-x0,y0).
因为M,N分别是OP,BP的中点,
所以M点的坐标为x02,y02,N点的坐标为x02,y0-12.
所以直线AD的方程为y=y0-2x0x+1.
将其代入椭圆方程x24+y2=1中,
得[x02+4(y0-2)2]x2+8x0(y0-2)x=0.
所以x=0,或x=8x0(2-y0)x02+4(y0-2)2=2x0(2-y0)5-4y0.
所以y=y0-2x0·2x0(2-y0)5-4y0+1=-2y02+4y0-35-4y0.
所以点D的坐标为2x0(2-y0)5-4y0,-2y02+4y0-35-4y0.
所以kQD=-2y02+4y0-35-4y0-y02x0(2-y0)5-4y0+x0=-y0+13x0.
又kQN=y0-12-y0x02+x0=-y0+13x0,
所以kQN=kQD,
所以D,N,Q三点共线.
思路分析 第(2)问要证D、N、Q三点共线,只需证明kQN=kQD即可,设出点P的坐标后,可知点Q的坐标,利用中点坐标公式可知点N的坐标,再利用直线方程求点D的坐标,最后验证kQN=kQD.