2018-2019学年江西省樟树中学高二上学期第一次月考数学（文）试题（Word版）

2018-2019学年江西省樟树中学高二上学期第一次月考数学（文）试题（Word版）

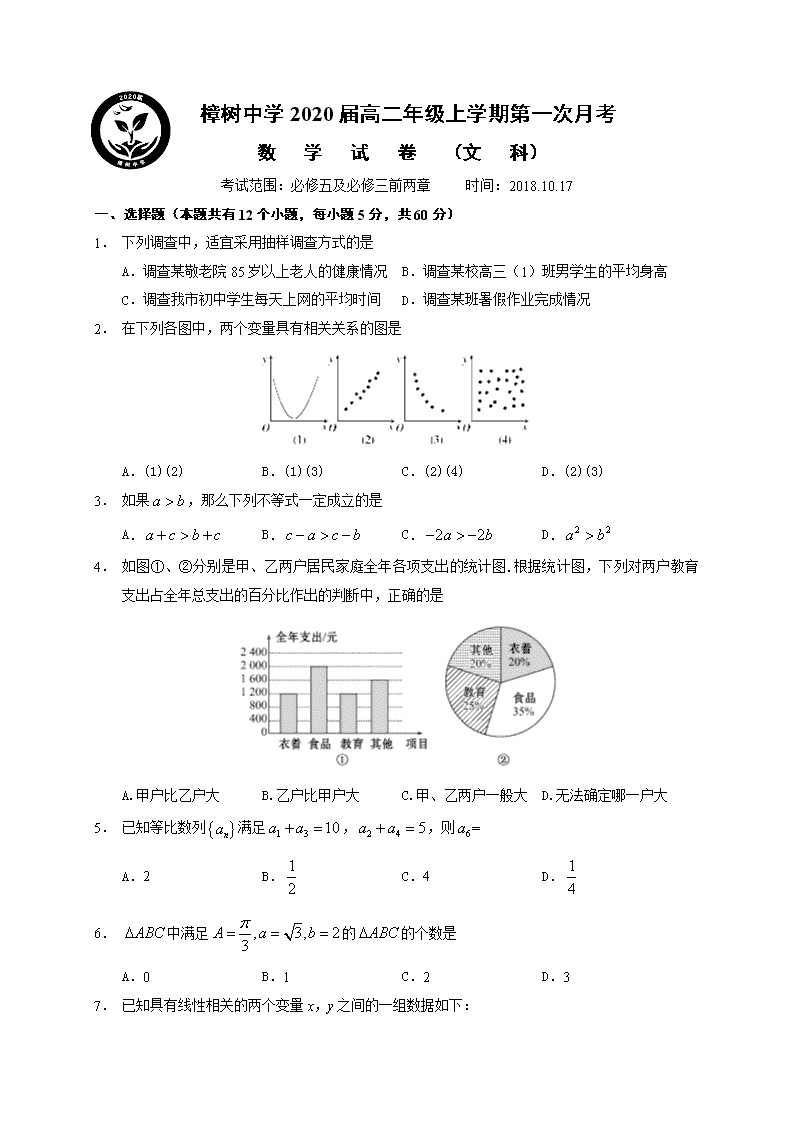
‎ 樟树中学2020届高二年级上学期第一次月考 ‎ 数 学 试 卷 （文 科）‎ 考试范围：必修五及必修三前两章 时间：2018.10.17‎ 一、选择题（本题共有12个小题，每小题5分，共60分）‎ 1． 下列调查中，适宜采用抽样调查方式的是 A．调查某敬老院85岁以上老人的健康情况 B．调查某校高三（1）班男学生的平均身高 C．调查我市初中学生每天上网的平均时间 D．调查某班暑假作业完成情况 2． 在下列各图中，两个变量具有相关关系的图是 A．(1)(2) B．(1)(3) C．(2)(4) D．(2)(3)‎ 3． 如果，那么下列不等式一定成立的是 A． B． C． D．‎ 4． 如图①、②分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图，下列对两户教育支出占全年总支出的百分比作出的判断中，正确的是 A.甲户比乙户大 B.乙户比甲户大 C.甲、乙两户一般大 D.无法确定哪一户大 5． 已知等比数列满足，，则=‎ A．2 B． C．4 D．‎ 6． 中满足的的个数是 A．0 B．1 C．2 D．3‎ 7． 已知具有线性相关的两个变量x，y之间的一组数据如下：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ a b c d e 且回归方程是，则 A．2 B．3 C．4 D．5‎ 1． 设，满足约束条件，若取得最大值的最优解不唯一，‎ 则实数的值为 A．或 B．或 ‎ C．或 D．或2‎ 2． 右图中茎叶图记录了某学习小组 学生数学考试成绩，1号到16号 同学的成绩依次为A1，A2，…，‎ A16，算法流程图用来统计茎叶图 中成绩在一定范围内的学生人数，‎ 那么该算法流程图输出的结果是 A．6 B．10 C．91 D．92‎ 3． 已知数列为正项等差数列，其前9项和，则的最小值为 A．1 B．16 C．9 D．4‎ 4． 中，已知分别为角的对边且，若，‎ ‎,则的周长等于 A． B．14 C． D．18‎ 5． 已知函数是奇函数，当，若不等式且对恒成立，则实数的取值范围是 A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ 6． 不等式的解集为________．‎ 7． 已知一组数据为0，3，5，x，7，13，且这组数据的中位数为6，那么这组数据的众数为________．‎ 1． 用系统抽样法(按照加抽样距的规则)从160名学生中抽取容量为20的样本，将这160名 学生从1到160编号．按编号顺序平均分成20段(1～8号，9～16号，…，153～160号)，‎ 若第17段应抽出的号码为135，则第1段中用简单随机抽样确定的号码是________．‎ 2． 已知方程： ，其一根在区间内，另一根在区间内，‎ 则的取值范围为________．‎ 三、解答题（本大题有6个小题，共70分）‎ 1． ‎（本小题满分10分）‎ 某货轮在A处看灯塔B在货轮的北偏东的方向上，距离为海里，在A处看灯塔C在货轮的北偏西的方向上，距离为8海里，货轮由A处向正北航行到D处时，再看灯塔B在南偏东方向上，求：‎ ‎（1）AD的距离；‎ ‎（2）CD的距离．‎ 2． ‎（本小题满分12分）‎ 某研究机构对高二学生的记忆力x和判断力y进行统计分析，得下表数据 x ‎6‎ ‎8‎ ‎10‎ ‎12‎ y ‎2‎ ‎3‎ ‎5‎ ‎6‎ ‎（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；‎ ‎（2）试根据（1）求出的线性回归方程，预测记忆力为7的同学的判断力．‎ ‎（）‎ 3． ‎（本小题满分12分）‎ 如图，某广场要划定一矩形区域ABCD，并在该区域内开辟出三块形状大小相同的矩形绿化区，这三块绿化区四周和绿化区之间设有1米宽的走道．已知三块绿化区的总面积为800‎ 平方米，求该矩形区域ABCD占地面积的最小值．‎ 1． ‎（本小题满分12分）‎ 某剧团在某场演出结束后从观众中随机抽取60人进行访谈，将观众的满意度分成六段：，，…，后得到如下频率分布直方图．‎ ‎（1）求满意度在内的频率；‎ ‎（2）用分层抽样的方法在这60名观众中抽取 一个容量为20的样本，则各数据段抽取 的人数分别是多少？‎ ‎（3）若所有观众中满意度大于b的人数占总 人数的40％，根据频率分布直方图估计 b的值（小数点后保留一位有效数字）．‎ 2． ‎（本小题满分12分）‎ 若数列的首项为1，且.‎ ‎（1）令，求证：是等比数列；‎ ‎（2）求数列的通项公式；‎ ‎（3）若，求证：数列的前项和.‎ 3． ‎（本小题满分12分）‎ 已知二次函数满足：①当时，恒成立；②对任意 实数，都有.‎ ‎（1）求；‎ ‎（2），求；‎ ‎（3）在（2）的条件下，设，若直线 图像位于图像下方，求实数m的取值范围.‎ 樟树中学2020届高二年级上学期第一次月考数学参考答案（文科）‎ ‎1-12．CDAB DBCA ABAC 13． 14．7 15．7 16．‎ ‎17．解：（1）在△ABD中，由已知得∠ADB=60°，B=45°‎ 由正弦定理得……5分 ‎（2）在中，由余弦定理得CD2=AD2+AC2-2AD.ACcos30°，解得CD=8．‎ 所以A处与D处之间的距离为海里，灯塔C与D处之间的距离为8海里……10分 ‎18．解：（1）‎ ‎=，=，‎ 代入公式求得：，‎ 故线性回归方程为……8分 ‎（2）解：由回归直线方程预测，记忆力为7的同学的判断力约为2.6……12分 ‎19．解：设绿化区域小矩形的一边长为x，另一边长为y，‎ ‎ 则3xy＝800，所以，‎ 所以矩形区域ABCD的面积 S＝(3x+4)(y+2)，‎ 当且仅当，即时取“＝”，‎ 即矩形区域ABCD的面积的最小值为968平方米．……12分 ‎20．解：（1）所求频率为1-0.1-0.15-0.15-0.25-0.05=0.3‎ ‎（2）各层抽取比例为，各层人数分别为6,9,9,18,15,3，所以抽取人数依次为2人；‎ ‎3人；3人；6人；5人；1人 ‎（3）各个分组的频率从左到右记为，，则 ‎ 而，∴‎ ‎∴估计 ‎21．解：（1）由得∴∴，‎ ‎∴，∴是首项为公比为的等比数列……4分 ‎（2）由（1）知，∴……8分 ‎（3）∵‎ ‎，‎ ‎∴‎ ‎∴.……12分 ‎22．解：（1）设，条件知恒成立，‎ 又恒成立∴.……4分 ‎（2）‎ 又即恒成立 解得：，.……8分 ‎（3）由题意知在上恒成立，‎ 即在上恒成立.‎ ‎①由，即，又∵∴解得：；‎ ‎②由，经计算无解；‎ 综合①②得.……12分 （参变分离也可以）‎