【数学】2018届一轮复习新人教B版第2讲常用逻辑知识教案

【数学】2018届一轮复习新人教B版第2讲常用逻辑知识教案

常用逻辑知识 课标要 求 ‎1．命题及其关系 ‎① 了解命题的逆命题、否命题与逆否命题；‎ ‎② 理解必要条件、充分条件与充要条件的意义，会分析四种命题的相互关系；‎ ‎2．简单的逻辑联结词 通过数学实例，了解"或"、"且"、"非"逻辑联结词的含义。‎ ‎3．全称量词与存在量词 ‎① 通过生活和数学中的丰富实例，理解全称量词与存在量词的意义；‎ ‎② 能正确地对含有一个量词的命题进行否定。‎ 命题走 向 本部分内容主要是常用的逻辑用语，包括命题与量词，基本逻辑联结词以及充分条件、必要条件与命题的四种形式。‎ 预测2017年高考对本部分内容的考查形式如下：考查的形式以选择、填空题为主，考察的重点是条件和复合命题真值的判断。‎ 教学准备 多媒体 教学过程 要点精讲:‎ ‎1．命题 命题：可以判断真假的语句叫命题；‎ 逻辑联结词：“或”“且”“非”这些词就叫做逻辑联结词；简单命题：不含逻辑联结词的命题。复合命题：由简单命题与逻辑联结词构成的命题。‎ 常用小写的拉丁字母p，q，r，s，……表示命题，故复合命题有三种形式：p或q；p且q；非p。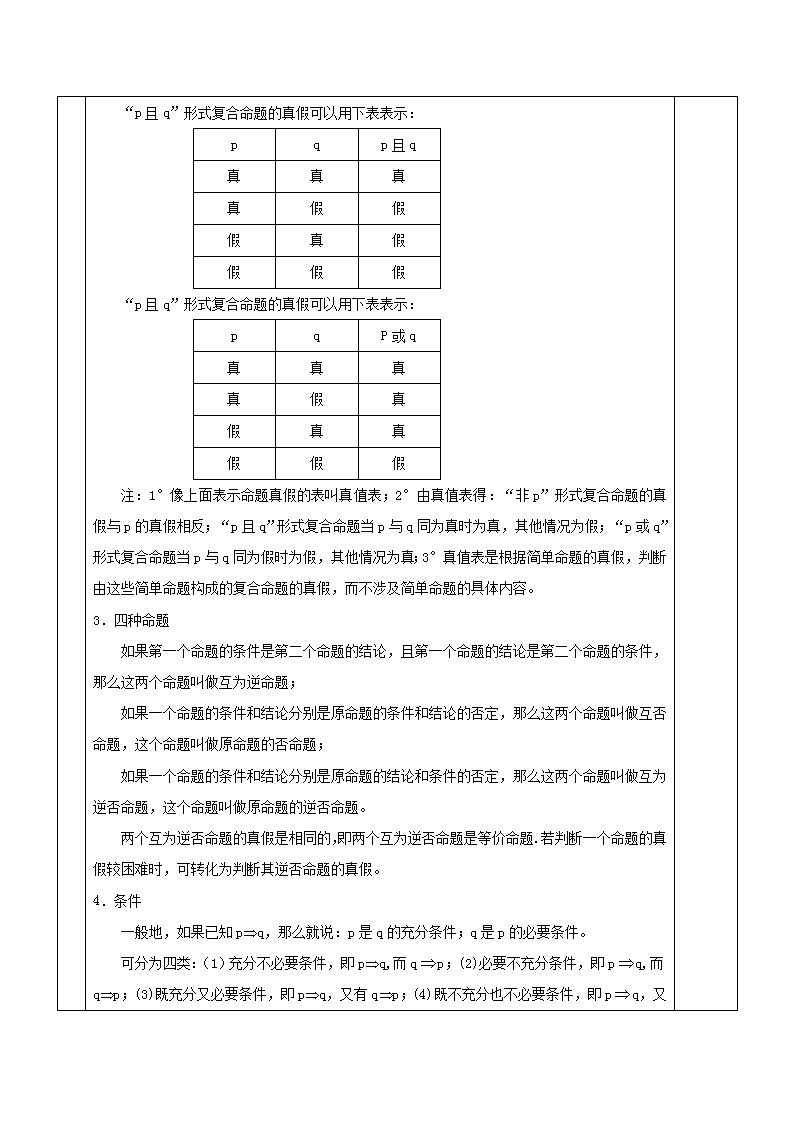‎ ‎2．复合命题的真值 ‎“非p”形式复合命题的真假可以用下表表示： ‎ p 非p 真 假 假 真 ‎“p且q”形式复合命题的真假可以用下表表示：‎ p q p且q 真 真 真 真 假 假 假 真 假 假 假 假 ‎“p且q”形式复合命题的真假可以用下表表示：‎ p q P或q 真 真 真 真 假 真 假 真 真 假 假 假 注：1°像上面表示命题真假的表叫真值表；2°由真值表得：“非p”形式复合命题的真假与p的真假相反；“p且q”形式复合命题当p与q同为真时为真，其他情况为假；“p或q”形式复合命题当p与q同为假时为假，其他情况为真；3°真值表是根据简单命题的真假，判断由这些简单命题构成的复合命题的真假，而不涉及简单命题的具体内容。‎ ‎3．四种命题 如果第一个命题的条件是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互为逆命题；‎ 如果一个命题的条件和结论分别是原命题的条件和结论的否定，那么这两个命题叫做互否命题，这个命题叫做原命题的否命题；‎ 如果一个命题的条件和结论分别是原命题的结论和条件的否定，那么这两个命题叫做互为逆否命题，这个命题叫做原命题的逆否命题。‎ 两个互为逆否命题的真假是相同的，即两个互为逆否命题是等价命题.若判断一个命题的真假较困难时，可转化为判断其逆否命题的真假。‎ ‎4．条件 一般地，如果已知pÞq，那么就说：p是q的充分条件；q是p的必要条件。‎ 可分为四类：（1）充分不必要条件，即pÞq,而qp；(2)必要不充分条件，即pq,而qÞp；(3)既充分又必要条件，即pÞq，又有qÞp；(4)既不充分也不必要条件，即p q，又有qp。‎ 一般地，如果既有pÞq，又有qÞp，就记作：pq.“”叫做等价符号。pq表示pÞq且qÞp。‎ 这时p既是q的充分条件，又是q的必要条件，则p是q的充分必要条件，简称充要条件。‎ ‎5．全称命题与特称命题 这里，短语“所有”在陈述中表示所述事物的全体，逻辑中通常叫做全称量词，并用符号表示。含有全体量词的命题，叫做全称命题。‎ 短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词，并用符号表示，含有存在量词的命题，叫做存在性命题。‎ 典例解析：‎ ‎1．(教材习题改编)下列命题是真命题的为(　　)‎ A．若＝，则x＝y　　　　 B．若x2＝1，则x＝1‎ C．若x＝y，则＝ D．若xb”是“a2>b‎2”‎的充分条件；‎ ‎②“|a|>|b|”是“a2>b‎2”‎的必要条件；‎ ‎③“a>b”是“a＋c>b＋c”的充要条件．‎ 解析：①由2>－3⇒/ 22>(－3)2知，该命题为假；②由a2>b2⇒|a|2>|b|2⇒|a|>|b|知，该命题为真；③a>b⇒a＋c>b＋c，又a＋c>b＋c⇒a>b，∴“a>b”是“a＋c>b＋c”的充要条件为真命题．‎ 答案：②③‎ ‎　　1.充分条件与必要条件的两个特征 ‎ (1)对称性：若p是q的充分条件，则q是p的必要条 件，即“p⇒q”⇔“q⇐p”；‎ ‎ (2)传递性：若p是q的充分(必要)条件，q是r的充分 ‎(必要)条件，则p是r的充分(必要)条件．‎ ‎ 注意区分“p是q的充分不必要条件”与“p的一个充分 不必要条件是q”两者的不同，前者是“p⇒q”而后者是 ‎“q⇒p”．‎ ‎ 2．从逆否命题，谈等价转换 ‎ 由于互为逆否命题的两个命题具有相同的真假性，因而，‎ 当判断原命题的真假比较困难时，可转化为判断它的逆否命 题的真假，这就是常说的“正难则反”．‎ 四种命题的关系及真假判断 典题导入 ‎　下列命题中正确的是(　　)‎ ‎①“若x2＋y2≠0，则x，y不全为零”的否命题；‎ ‎②“正多边形都相似”的逆命题；‎ ‎③“若m>0，则x2＋x－m＝0有实根”的逆否命题；‎ ‎④“若x－3是有理数，则x是无理数”的逆否命题．‎ A．①②③④　　　　　　 B．①③④‎ C．②③④ D．①④‎ ‎　①中否命题为“若x2＋y2＝0，则x＝y＝‎0”‎，正确；③中，Δ＝1＋‎4m，当m>0时，Δ ‎>0，原命题正确，故其逆否命题正确；②中逆命题不正确；④中原命题正确故逆否命题正确．‎ ‎　B 由题悟法 在判断四个命题之间的关系时，首先要分清命题的条件与结论，再比较每个命题的条件与结论之间的关系．要注意四种命题关系的相对性，一旦一个命题定为原命题，也就相应的有了它的“逆命题”“否命题”“逆否命题”；判定命题为真命题时要进行推理，判定命题为假命题时只需举出反例即可．对涉及数学概念的命题的判定要从概念本身入手．‎ 以题试法 ‎1．以下关于命题的说法正确的有________(填写所有正确命题的序号)．‎ ‎①“若log‎2a>0，则函数f(x)＝logax(a>0，a≠1)在其定义域内是减函数”是真命题；‎ ‎②命题“若a＝0，则ab＝‎0”‎的否命题是“若a≠0，则ab≠‎0”‎；‎ ‎③命题“若x，y都是偶数，则x＋y也是偶数”的逆命题为真命题；‎ ‎④命题“若a∈M，则b∉M”与命题“若b∈M，则a∉M”等价．‎ 解析：对于①，若log‎2a>0＝log21，则a>1，所以函数f(x)＝logax在其定义域内是增函数，故①不正确；对于②，依据一个命题的否命题的定义可知，该说法正确；对于③，原命题的逆命题是“若x＋y是偶数，则x、y都是偶数”，是假命题，如1＋3＝4是偶数，但3和1均为奇数，故③不正确；对于④，不难看出，命题“若a∈M，则b∉M”与命题“若b∈M，则a∉M”是互为逆否命题，因此二者等价，所以④正确．综上可知正确的说法有②④.‎ 答案：②④‎ 充分必要条件的判定 典题导入 ‎　(1)(2012·福州质检)“x<‎2”‎是“x2－2x<‎0”‎的(　　)‎ A．充分而不必要条件　　 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎(2)(2012·北京高考)设a，b∈R，“a＝‎0”‎是“复数a＋bi是纯虚数”的(　　)‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎　(1)取x＝0，则x2－2x＝0，故由x<2不能推出x2－2x<0；由x2－2x<0得03.‎ ‎1．(2011·北京高考)若p是真命题，q是假命题，则(　　)‎ A．p∧q是真命题　　　　　　 B．p∨q是假命题 C．綈p是真命题 D．綈q是真命题 答案：D　‎ ‎2．(教材习题改编)下列命题中的假命题是(　　)‎ A．∃x0∈R，x0＋＝2 B．∃x0∈R，sin x0＝－1‎ C．∀x∈R，x2>0 D．∀x∈R,2x>0‎ 答案：C　‎ ‎3．(2012·湖南高考)命题“∃x0∈∁RQ，x∈Q”的否定是(　　)‎ A．∃x0∉∁RQ，x∈Q B．∃x0∈∁RQ，x∉Q C．∀x∉∁RQ，x3∈Q D．∀x∈∁RQ，x3∉Q 解析：选D　其否定为∀x∈∁RQ，x3∉Q.‎ ‎4．(教材习题改编)命题p：有的三角形是等边三角形．命题綈p：__________________.‎ 答案：所有的三角形都不是等边三角形 ‎5．命题“∃x0∈R,2x－3ax0＋9<‎0”‎为假命题，则实数a的取值范围为________．‎ 解析：∃x0∈R,2x－3ax0＋9<0为假命题，则∀x∈R，2x2－3ax＋9≥0恒成立，有Δ＝‎9a2－72≤0，解得－2≤a≤2.‎ 答案：‎ ‎　　　1.逻辑联结词与集合的关系 ‎ “或、且、非”三个逻辑联结词，对应着集合运算中的 ‎“并、交、补”，因此，常常借助集合的“并、交、补”的 意义来解答由“或、且、非”三个联结词构成的命题问题．‎ ‎ 2．正确区别命题的否定与否命题 ‎ “否命题”是对原命题“若p，则q”的条件和结论分 别加以否定而得到的命题，它既否定其条件，又否定其结论；‎ ‎“命题的否定”即“非p”，只是否定命题p的结论．‎ ‎ 命题的否定与原命题的真假总是对立的，即两者中有且 只有一个为真，而原命题与否命题的真假无必然联系．‎ 含有逻辑联结词命题的真假判定 典题导入 ‎　(2012·齐齐哈尔质检)已知命题p：∃x0∈R，使tan x0＝1，命题q：x2－3x＋2<0的解集是{x|13x，B不正确；对于C，易知3x≠0，因此C正确；对于D，注意到lg 1＝0，因此D正确．‎ ‎　B 由题悟法 ‎1．全称命题真假的判断方法 ‎(1)要判断一个全称命题是真命题，必须对限定的集合M中的每一个元素x，证明p(x)成立；‎ ‎(2)要判断一个全称命题是假命题，只要能举出集合M中的一个特殊值x＝x0，使p(x0)不成立即可．‎ ‎2．特称命题真假的判断方法 要判断一个特称命题是真命题，只要在限定的集合M中，找到一个x＝x0，使p(x0)成立即可，否则这一特称命题就是假命题．‎ 以题试法 ‎2．(2012·湖南十二校联考)下列命题中的真命题是(　　)‎ A．∃x0∈R，使得sin x0cos x0＝ B．∃x0∈(－∞，0)，2x0>1‎ C．∀x∈R，x2≥x－1 D．∀x∈(0，π)，sin x>cos x 解析：选C　由sin xcos x＝，得sin 2x＝>1，故A错误；结合指数函数和三角函数的图象，可知B，D错误；因为x2－x＋1＝2＋>0恒成立，所以C正确．‎ 全称命题与特称命题的否定 典题导入 ‎　(2013·武汉适应性训练)命题“所有不能被2整除的整数都是奇数”的否定是(　　)‎ A．所有能被2整除的整数都是奇数 B．所有不能被2整除的整数都不是奇数 C．存在一个能被2整除的整数是奇数 D．存在一个不能被2整除的整数不是奇数 ‎　命题“所有不能被2整除的整数都是奇数”的否定是“存在一个不能被2整除的整数不是奇数”，选D.‎ 若命题改为“存在一个能被2整除的整数是奇数”，其否定为________．‎ 答案：所有能被2整除的整数都不是奇数 由题悟法 ‎1．弄清命题是全称命题还是特称命题是写出命题否定的前提．‎ ‎2．注意命题所含的量词，没有量词的要结合命题的含义加上量词，再进行否定．‎ ‎3．要判断“綈p”命题的真假，可以直接判断，也可以判断“p”的真假，p与綈p的真假相反．‎ ‎4．常见词语的否定形式有：‎ 原语句 是 都是 ‎>‎ 至少有一个 至多有一个 对任意x∈A使p(x)真 否定形式 不是 不都是 ‎≤‎ 一个也没有 至少有两个 存在x0∈A使p(x0)假 以题试法 ‎3．(2012·辽宁高考)已知命题p：∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≥0，则綈p是(　　)‎ A．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0‎ B．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0‎ C．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0‎ D．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0‎ 解析：选C　命题p的否定为“∃x1，x2∈R，(f(x2)－f( x1))(x2－x1)<‎0”‎．‎ 需要用具体例子说明至少、至多的含义。‎ 板书设计 常用逻辑知识 ‎1．命题及其关系 两个互为逆否命题的真假是相同的， 例1‎ 即两个互为逆否命题是等价命题. 例2‎ 若判断一个命题的真假较困难时， 例3‎ 可转化为判断其逆否命题的真假。 例4‎ ‎2．简单的逻辑联结词 ‎"或"、"且"、"非"‎ ‎3．全称量词与存在量词 全称命题的否定是特称命题，‎ 特称命题的否定是全称命题。‎ 教学反思 ‎ 学生对逻辑知识本身掌握情况较好，但涉及与其他知识结合的题目时，学生往往出现困难，困难的原因是学生对其他相关知识遗忘的较多。因此，复习本部分知识前，适当复习回顾有关知识是必要的。‎