惠州市2020届高三第二次调研考试 理科数学 试题

惠州市2020届高三第二次调研考试 理科数学 试题

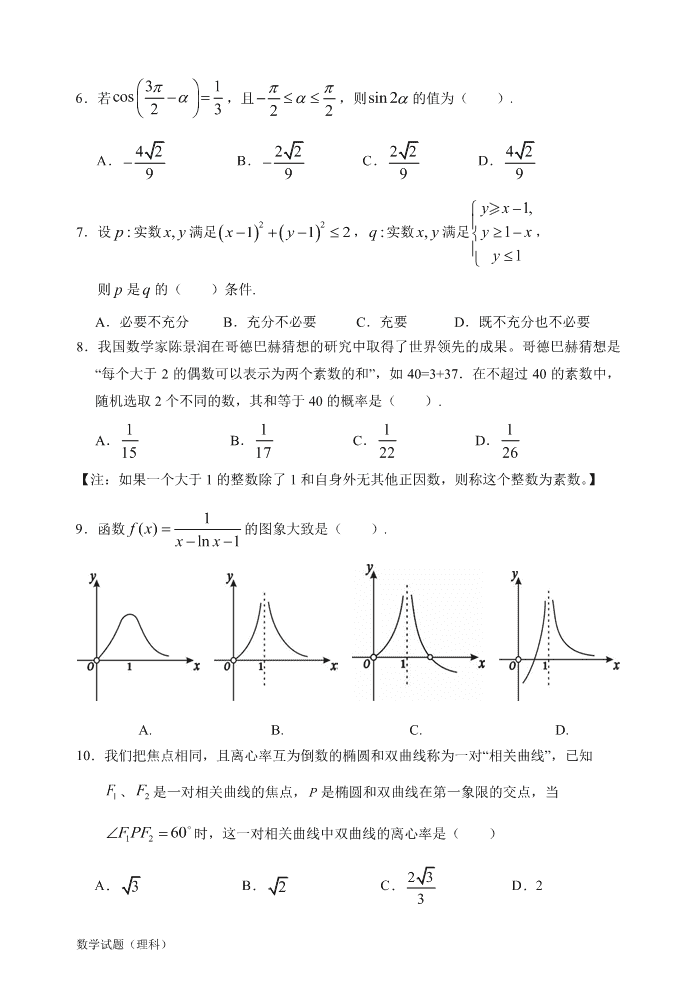
数学试题（理科） 惠州市 2020 届高三第二次调研考试 理科数学 2019.10 全卷满分 150 分，时间 120 分钟． 注意事项： 1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填 写在答题卡上。 2．作答选择题时，选出每个小题答案后，用 2B 铅笔把答题卡上对应题目的答案信 息点涂黑。如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。 3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上， 写在本试卷上无效。 一、选择题：本题共 12 小题，每小题 5 分，共 60 分. 在每小题给出的四个选项中，只有 一项符合题目要求. 1．集合 M＝{x | lg x > 0}，N＝{x | x2 ≤ 4}，则 M ∩ N＝（ ）. A．(-2,0) B．[1,2) C．(1,2] D．(0,2] 2．设复数 z 满足(1 ) 1i z i （其中i 为虚数单位），则 z （ ）. A． i B．i C． 2i D． 2i 3．已知 nS 为数列{}na 的前 n 项和， 1nnSa，则 5S （ ）. A． 31 16 B． 31 2 C． 1 32 D． 31 32 4．已知 ,ab为互相垂直的单位向量，若 =−c a b，则cos ,bc （ ）. A． 2 2 B． 2 2 C． 3 3 D． 3 3 5．下列说法正确的是（ ） ①从匀速传递的产品生产流水线上，质检员每 10 分钟从中抽取一件产品进行某项指 标检测，这样的抽样是分层抽样． ②某地气象局预报：5 月 9 日本地降水概率为 90%，结果这天没下雨，这表明天气预 报并不科学． ③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好． ④在回归直线方程 中，当解释变量 x 每增加 1 个单位时，预报变量 增 加 0.1 个单位． A．①② B．③④ C．①③ D．②④ 101.0ˆ += xy yˆ 数学试题（理科） 6．若 31cos 23  −= ，且 22 −   ，则sin 2 的值为（ ）. A． 42 9− B． 22 9− C． 22 9 D． 42 9 7．设 :p 实数 ,xy满足( ) ( )221 1 2xy− + −  ， :q 实数 ,xy满足 1, 1 1 yx yx y −  −   ， 则 p 是 q 的（ ）条件. A．必要不充分 B．充分不必要 C．充要 D．既不充分也不必要 8．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。哥德巴赫猜想是 “每个大于 2 的偶数可以表示为两个素数的和”，如 40=3+37．在不超过 40 的素数中， 随机选取 2 个不同的数，其和等于 40 的概率是（ ）. A． 1 15 B． 1 17 C． 1 22 D． 1 26 【注：如果一个大于 1 的整数除了 1 和自身外无其他正因数，则称这个整数为素数。】 9．函数 1() ln 1fx xx= −− 的图象大致是（ ）. A. B. C. D. 10．我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”，已知 1F 、 2F 是一对相关曲线的焦点， P 是椭圆和双曲线在第一象限的交点，当 1260F PF=时，这一对相关曲线中双曲线的离心率是（ ） A． 3 B． 2 C． 23 3 D．2 数学试题（理科） 11．已知矩形 ABCD， 1AB = ， 3BC = ，将 ADC 沿对角线 AC 进行翻折，得到三 棱锥 D ABC− ，则在翻折的过程中，有下列结论： ①三棱锥 D ABC− 的体积最大值为 3 1 ； ②三棱锥 D ABC− 的外接球体积不变； ③三棱锥 D ABC− 的体积最大值时，二面角 D AC B−−的大小是 60°； ④异面直线 AB 与CD 所成角的最大值为90 ． 其中正确的是（ ）. A．①②④ B．②③ C．②④ D．③④ 12．设函数 m xxf sin3)( = ，若存在 )(xf 的极值点 0x 满足   22 0 2 0 )( mxfx + ， 则 m 的取值范围是（ ）. A．(－∞，－6)∪(6，＋∞) B．(－∞，－4)∪(4，＋∞) C．(－∞，－2)∪(2，＋∞) D．(－∞，－1)∪(1，＋∞) 二．填空题：本题共4小题，每小题5分，共20分，其中第15题第一空3分，第二空2分。 13．已知函数 3( ) lnf x ax x 的图象在点(1, (1))f 处的切线斜率为 2， 则 a 的值等于_________． 14．某工厂为了解产品的生产情况，随机抽取了 100 个样本。若样本数据 1x ， 2x ，， 100x 的方差为8 ，则数据 121x − ， 221x − ，， 10021x − 的方差为_________． 15．设 x 、 y 为正数，若 12 yx +=，则 12 xy+ 的最小值是 ，此时 x = ． 16．已知椭圆 ( ) 22 2210xy abab+ =   的短轴长为 2，上顶点为 A ，左顶点为 B ，左、右 焦点分别是 1F ， 2F ，且 1F AB△ 的面积为 23 2 − ，点 P 为椭圆上的任意一点， 则 12 11 PF PF+ 的取值范围是 . 数学试题（理科） 三．解答题：共70分，解答应写出文字说明，证明过程或演算步骤。第17～21题为必考 题，每个考生都必须作答。第22、23题为选考题，考生根据要求作答。 （一）必考题：共60分。 17．（本小题满分 12 分） 在 ABC 中，角 ,,A B C 的对边分别为 , ,cab ，已知 2a ， 5b = ， 2BA= ． （1）求 cos A； （2）求 c 边的值． 18．（本小题满分 12 分） 在数列{}na 中， 1 1a ， 2 8 3a ， 1 111nnn naan + += + + ，其中 *nN ， 为常 数． （1）求 的值； （2）设 n n ab n ，求数列{}nb 的通项公式． 19．（本小题满分 12 分） 如图，在底面为矩形的四棱锥 P ABCD 中，平面 PAD 平面 ABCD． （1）证明： AB PD； （2）若 , 90PA PD AB APD ，设Q 为 PB 中点， 求直线 AQ 与平面 PBC 所成角的余弦值． P A B C D 数学试题（理科） 20．（本小题满分 12 分） 已知抛物线 2:2C y x 的焦点为 F ，直线l 与C 交于 ,AB两点，且与 x 轴交于点 ( ,0)Pa ． （1）若直线l 的斜率 3 2k ，且 3 2FP ，求 AF BF 的值； （2）若 0a  ， x 轴上是否存在点 M ，总有 OMA OMB ？ 若存在，求出点 M 坐标；若不存在，请说明理由． 数学试题（理科） 数学试题（理科） 21．（本小题满分 12 分） 已知函数 1 2 2( ) ln xef x a x xx −= + − （ a 为常数）在区间( )0,2 内有两个极值点 ( )1 2 1 2,x x x x ． （1）求实数 a 的取值范围； （2）求证： ( )122 1 lnx x a+  + ． 数学试题（理科） 23．（本小题满分 10 分）[选修 4-5：不等式选讲] 已知关于 x 的不等式 20x m x− +  的解集为{ | 2}xx− ，其中 0m  . （1）求 m 的值； （2）若正数 a 、b 、 c 满足 a b c m+ + = ，求证： 2 2 2 2b c a a b c+ +  . （二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的 第一题计分。答题时请写清题号并将相应信息点涂黑。 22．（本小题满分 10 分）[选修 4-4：坐标系与参数方程] 已知在平面直角坐标系 xOy 中，圆C 的参数方程为 cos 1 sin x y   =  =+ ( 为参数) ．以原 点O 为极点， x 轴的非负半轴为极轴，取相同的单位长度建立极坐标系． （1）求圆C 的普通方程及其极坐标方程； （2）设直线l 的极坐标方程为 sin( ) 23 +=，射线 : 6OM  = 与圆C 的交点为 P （异于极点），与直线l 的交点为 Q，求线段 PQ 的长．