数学文卷·2018届湖北省枣阳市白水高级中学高二12月月考（2016-12）

数学文卷·2018届湖北省枣阳市白水高级中学高二12月月考（2016-12）

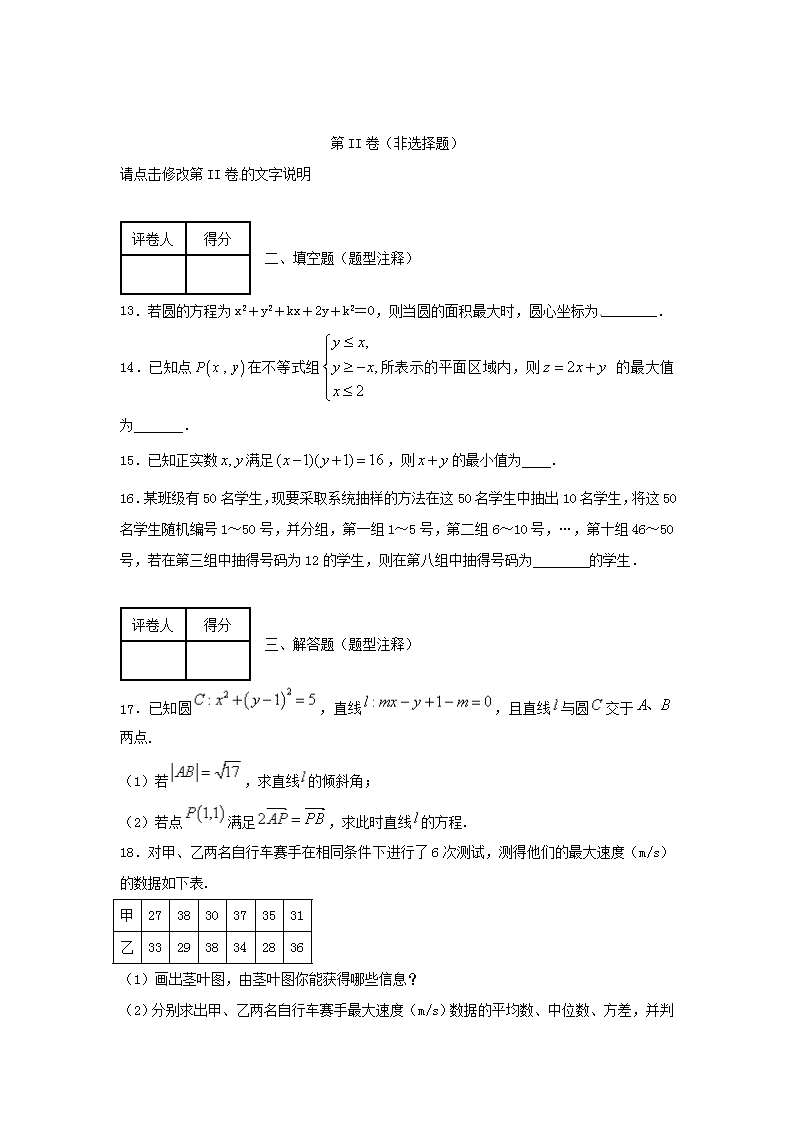
枣阳市白水高中2016-2017学年度高二文科数学12月月考卷 ‎★祝考试顺利★‎ 时间：120分钟 分值150分_‎ 第I卷（选择题共60分）‎ 一、选择题（本大题12小题，每小题5分，共60分）‎ ‎1．已知倾斜角为的直线与直线平行，则tan2的值(    )‎ A． B． C． D．‎ ‎2．点M(x，y)在函数y=－2x+8的图象上，当x∈时，的取值范围是(　　)‎ A． B．‎ C． D．‎ ‎3．两条平行直线和之间的距离是（ ）‎ A． B． C． D．‎ ‎4．已知直线与平行，则的值是（ ）‎ A．0或1 B．1或 C．0或 D．‎ ‎5．直线x－2y＋1＝0关于直线x＝1对称的直线方程是(　　)‎ A.x＋2y－1＝0 B.2x＋y－1＝0‎ C.2x＋y－3＝0 D.x＋2y－3＝0‎ ‎6．已知点在直线上，则的最小值为（ ）‎ A． B． C． D．‎ ‎7．已知和是平面内互相垂直的两条直线，它们的交点为A，异于点A的两动点B、C分别在、上，且BC=3，则过A、B、C三点的圆面积为（ ）‎ A． B． C． D．‎ ‎8．当时，的最小值为（ ）‎ A．10 B．‎12 C．14 D．16‎ ‎9．（5分）（2011•陕西）如图框图，当x1=6，x2=9，p=8.5时，x3等于（ ）‎ A.7 B‎.8 C.10 D.11‎ ‎10．某防疫站对学生进行身体健康调查，欲采用分层抽样的办法抽取样本．某中学共有学生名，抽取了一个容量为的样本，已知样本中女生比男生少人，则该校共有女生（ ）‎ A．人 B．人 C．人 D．人 ‎11．下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是( )‎ A.30.5 B‎.31 ‎‎ ‎‎ C.31.5 D.32‎ ‎12． 由变量与相对应的一组数据、、、、‎ 得到的线性回归方程为，则（ ）‎ A、 B、 C、 D、‎ 第II卷（非选择题）‎ 请点击修改第II卷的文字说明 评卷人 得分 二、填空题（题型注释）‎ ‎13．若圆的方程为x2＋y2＋kx＋2y＋k2＝0，则当圆的面积最大时，圆心坐标为________．‎ ‎14．已知点在不等式组所表示的平面区域内，则 的最大值为 ．‎ ‎15．已知正实数满足，则的最小值为 ．‎ ‎16．某班级有50名学生，现要采取系统抽样的方法在这50名学生中抽出10名学生，将这50名学生随机编号1～50号，并分组，第一组1～5号，第二组6～10号，…，第十组46～50号，若在第三组中抽得号码为12的学生，则在第八组中抽得号码为　 　的学生．‎ 评卷人 得分 三、解答题（题型注释）‎ ‎17．已知圆，直线，且直线与圆交于两点.‎ ‎（1）若，求直线的倾斜角；‎ ‎（2）若点满足，求此时直线的方程.‎ ‎18．对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表.‎ 甲 ‎27‎ ‎38‎ ‎30‎ ‎37‎ ‎35‎ ‎31‎ 乙 ‎33‎ ‎29‎ ‎38‎ ‎34‎ ‎28‎ ‎36‎ ‎（1）画出茎叶图，由茎叶图你能获得哪些信息？‎ ‎（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、方差，并判断选谁参加比赛更合适.‎ ‎19．已知等差数列满足：，，其前项和为.‎ ‎(1）求数列的通项公式及；‎ ‎(2）若等比数列的前项和为，且，，求.‎ ‎20．在△ABC中，角A，B，C所对的边分别为a，b，c，且＋1＝．‎ ‎（1）求B；‎ ‎（2）若cos(C＋)＝，求sinA的值．‎ ‎21．如图所示，四棱锥中，底面是边长为的正方形，侧棱底面，且，是的中点．‎ ‎（1）证明：平面；‎ ‎（2）求三棱锥的体积．‎ ‎22．已知以点为圆心的圆与直线相切，过点的动直线与圆相交于两点.‎ ‎（1）求圆的方程；‎ ‎（2）当时，求直线的方程 答案 选择：1_5 BCACD 6_10ABDBD 11_12BD ‎ 填空：‎ ‎13．若圆的方程为x2＋y2＋kx＋2y＋k2＝0，则当圆的面积最大时，圆心坐标为________．‎ ‎【答案】(0，－1)‎ ‎14．已知点在不等式组所表示的平面区域内，则 的最大值为 ．‎ ‎【答案】6．‎ ‎15．已知正实数满足，则的最小值为 ．‎ ‎16．某班级有50名学生，现要采取系统抽样的方法在这50名学生中抽出10名学生，将这50名学生随机编号1～50号，并分组，第一组1～5号，第二组6～10号，…，第十组46～50号，若在第三组中抽得号码为12的学生，则在第八组中抽得号码为　 　的学生．‎ ‎【答案】37‎ ‎17．已知圆，直线，且直线与圆交于两点.‎ ‎（1）若，求直线的倾斜角；‎ ‎（2）若点满足，求此时直线的方程.‎ ‎【答案】（1）或；（2）或. ‎ ‎18．对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表.‎ 甲 ‎27‎ ‎38‎ ‎30‎ ‎37‎ ‎35‎ ‎31‎ 乙 ‎33‎ ‎29‎ ‎38‎ ‎34‎ ‎28‎ ‎36‎ ‎（1）画出茎叶图，由茎叶图你能获得哪些信息？‎ ‎（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、方差，并判断选谁参加比赛更合适.‎ ‎19．已知等差数列满足：，，其前项和为.‎ ‎(1）求数列的通项公式及；‎ ‎(2）若等比数列的前项和为，且，，求.‎ ‎【答案】(1） ,;(2）‎ 试题分析：(1）由等差数列的通项公式,据已知的值,建立关于的方程组,解方程组可得,从而得到等差数列的通项公式和前项和公式;‎ ‎(2） 已知,由等比数列的通项公式,利用 求出,可得等比数列的前项和.‎ 试题解析:(1） 设等差数列的公差为，则， ‎ 解得：， ‎ ‎∴，‎ ‎(2）设等比数列的公比为，∵， ，∴，‎ ‎ ∴， ‎ ‎∴ ‎ ‎20．在△ABC中，角A，B，C所对的边分别为a，b，c，且＋1＝．‎ ‎（1）求B；‎ ‎（2）若cos(C＋)＝，求sinA的值．‎ ‎21．如图所示，四棱锥中，底面是边长为的正方形，侧棱底面，且，是的中点．‎ ‎（1）证明：平面；‎ ‎（2）求三棱锥的体积．‎ ‎【答案】（1）证明详见解析；（2）.‎ 试题分析：（1）要证平面，由于平面，故只须在平面内找到一条直线与平行即可，而这一条直线就是平面与平面的交线，故连接，设其交于点，进而根据平面几何的知识即可证明，从而就证明了平面；（2）根据已知条件及棱锥的体积计算公式可得，进而代入数值进行运算即可.‎ 试题解析：（1）证明：连结,交于 因为底面为正方形, 所以为的中点.又因为是的中点,‎ 所以 因为平面,平面, 所以平面 6分 ‎（2）因为侧棱底面，所以三棱锥的高为，而底面积为，所以 13分.‎ 考点：1.空间中的平行关系；2.空间几何体的体积.‎ ‎22．已知以点为圆心的圆与直线相切，过点的动直线与圆相交于两点.‎ ‎（1）求圆的方程；‎ ‎（2）当时，求直线的方程.‎ ‎【答案】（1）；（2）或