2018届二轮复习11-2古典概型课件（全国通用）

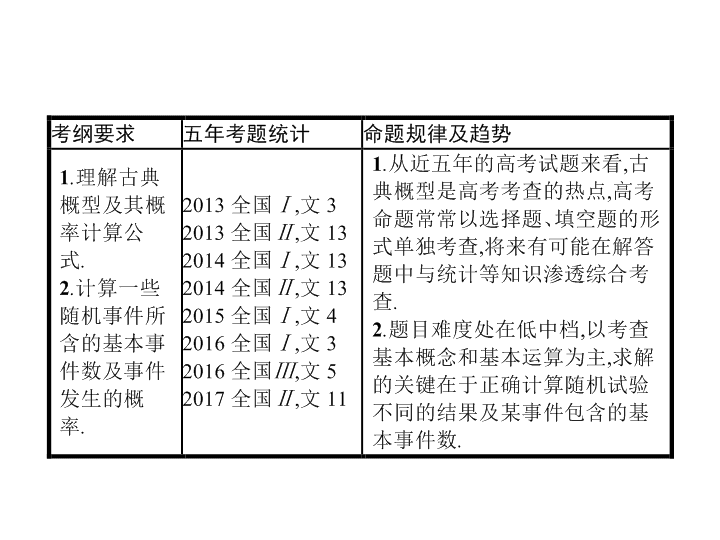
2018届二轮复习11-2古典概型课件（全国通用）

11 . 2 　 古典概型 - 2 - - 3 - 知识梳理 考点自测 1 . 基本事件的特点 (1) 任何两个基本事件是 　　　　 的 .   (2) 任何事件 ( 除不可能事件 ) 都可以表示成 　　　　　　　　 的和 .   2 . 古典概型 具有以下两个特点的概率模型称为古典概率模型 , 简称古典概型 . (1) 有限性 : 试验中所有可能出现的基本事件 　　　　　　　　 .   (2) 等可能性 : 每个基本事件出现的可能性 　　　　 .   3 . 古典概型的概率公式 互斥 基本事件 只有有限个 相等 - 4 - 知识梳理 考点自测 1 . 任一随机事件的概率都等于构成它的每一个基本事件概率的和 . 2 . 求试验的基本事件数及事件 A 包含的基本事件数的方法有列举法、列表法和树状图法 . - 5 - 知识梳理 考点自测 × √ × √ √ - 6 - 知识梳理 考点自测 B 解析 : 甲、乙、丙三人站成一排照相留念 , 站法有甲乙丙 , 甲丙乙 , 乙丙甲 , 乙甲丙 , 丙甲乙、丙乙甲 , 共 6 种 , 乙正好站在甲、丙之间的有甲乙丙 , 丙乙甲 , 共 2 种 , 故所求概率为 , 故选 B . - 7 - 知识梳理 考点自测 C 解析 : 从 5 支彩笔中任取 2 支不同颜色的彩笔 , 共有 ( 红黄 ),( 红蓝 ),( 红绿 ),( 红紫 ),( 黄蓝 ),( 黄绿 ),( 黄紫 ),( 蓝绿 ),( 蓝紫 ),( 绿紫 )10 种不同情况 , 记 “ 取出的 2 支彩笔中含有红色彩笔 ” 为事件 A , 则事件 A 包含 ( 红黄 ),( 红蓝 ),( 红绿 ),( 红紫 )4 个基本事件 , 则 . 故选 C . - 8 - 知识梳理 考点自测 C 解析 : 密码的前两位共有 15 种可能 , 其中只有 1 种是正确的密码 , 因此所求概率为 . 故选 C . - 9 - 知识梳理 考点自测 5 . (2017 江苏无锡一模 ,7) 从集合 {1,2,3,4} 中任取两个不同的数 , 则这两个数的和为 3 的倍数的槪率为 　　　　　 .   解析 : 从集合 {1,2,3,4} 中任取两个不同的数 , 基本事件总数 n= 6, 这两个数的和为 3 的倍数包含的基本事件有 (1,2),(2,4), 共 2 个 , 故这两个数的和为 3 的倍数的槪率 - 10 - 考点一 考点二 考点三 古典概型的概率 例 1 (1)(2017 全国 Ⅱ , 文 11) 从分别写有 1,2,3,4,5 的 5 张卡片中随机抽取 1 张 , 放回后再随机抽取 1 张 , 则抽得的第一张卡片上的数大于第二张卡片上的数的概率为 ( 　　 ) (2) 为美化环境 , 从红、黄、白、紫 4 种颜色的花中任选 2 种花种在一个花坛中 , 余下的 2 种花种在另一个花坛中 , 则红色和紫色的花不在同一花坛的概率是 ( 　　 ) D C - 11 - 考点一 考点二 考点三 解析 : (1) 由题意可得抽取两张卡片上的数的所有情况如下表所示 ( 表中点的横坐标表示第一次取到的数 , 纵坐标表示第二次取到的数 ): 总共有 25 种情况 , 其中第一张卡片上的数大于第二张卡片上的数的情况有 10 种 , 故所求的概率为 - 12 - 考点一 考点二 考点三 (2)( 解法一 ) 若认为两个花坛有区别 , 总的基本事件是 : 红黄 , 白紫 ; 白紫 , 红黄 ; 红白 , 黄紫 ; 黄紫 , 红白 ; 红紫 , 黄白 ; 黄白 , 红紫 , 共 6 种 . 满足条件的基本事件是 : 红黄 , 白紫 ; 白紫 , 红黄 ; 红白 , 黄紫 ; 黄紫 , 红白 , 共 4 种 . 故所求事件的概率为 ( 解法二 ) 若认为两个花坛没有区别 , 总的基本事件是 : 红黄 , 白紫 ; 红白 , 黄紫 ; 红紫 , 黄白 , 共 3 种 . 满足条件的基本事件是 : 红黄 , 白紫 ; 红白 , 黄紫 , 共 2 种 . 故所求事件的概率为 - 13 - 考点一 考点二 考点三 思考 求古典概型的概率的一般思路是怎样的 ? 对与顺序相关的问题怎样处理 ? 解题心得 1 . 求古典概型的概率的思路是 : 先求出试验的基本事件的总数和事件 A 包含的基本事件的个数 , 再代入古典概型的概率公式 . 2 . 对与顺序相关的问题处理方法为 : 若把顺序看作有区别 , 则在求试验的基本事件的总数和事件 A 包含的基本事件的个数时都看作有区别 , 反之都看作没区别 . - 14 - 考点一 考点二 考点三 对点训练 1 (1) 在 1,2,4,5 这 4 个数中一次随机地取 2 个数 , 则所取的 2 个数的和为 6 的概率为 ( 　　 ) (2)(2017 福建厦门一模 , 文 4) 中国将于 2017 年 9 月 3 日至 5 日在福建省厦门市主办金砖国家领导人第九次会晤 . 某志愿者队伍共有 5 人负责接待 , 其中 3 人担任英语翻译 , 另 2 人担任俄语翻译 . 现从中随机选取 2 人 , 恰有 1 个英语翻译 ,1 个俄语翻译的概率是 ( 　　 ) A C - 15 - 考点一 考点二 考点三 解析 : (1) 在 1,2,4,5 这 4 个数中一次随机地取 2 个数 , 总的基本事件有 (1,2),(1,4),(1,5),(2,4),(2,5),(4,5), 共 6 种 , 所取的 2 个数的和为 6 包含的基本事件有 (1,5),(2,4), 共 2 种 , 故所取的 2 个数的和为 6 的概率为 . 故选 A . (2) 从 5 人中随机选取 2 人的基本事件共有 10 个 , 恰有 1 个英语翻译 ,1 个俄语翻译的事件数为 6 个 , 所以所求概率为 , 故选 C . - 16 - 考点一 考点二 考点三 古典概型与其他知识的交汇问题 ( 多考向 )   考向 1 　 古典概型与平面向量的交汇 C 思考 如何把两个向量的夹角的范围问题转化成与求概率的基本事件有关的问题 ? - 17 - 考点一 考点二 考点三 考向 2 　 古典概型与解析几何的交汇 例 3 将一颗骰子先后投掷两次分别得到点数 a , b , 则直线 ax+by= 0 与圆 ( x- 2) 2 +y 2 = 2 有公共点的概率为 　　　　　 .   思考 如何把直线与圆有公共点的问题转化成与概率的基本事件有关的问题 ? - 18 - 考点一 考点二 考点三 考向 3 　 古典概型与函数的交汇 例 4 设 a ∈ {2,4}, b ∈ {1,3}, 函数 f ( x ) = ax 2 +bx+ 1 . (1) 求 f ( x ) 在区间 ( -∞ , - 1] 上是减函数的概率 ; (2) 从 f ( x ) 中随机抽取两个 , 求它们在 (1, f (1)) 处的切线互相平行的概率 . - 19 - 考点一 考点二 考点三 思考 如何把 f ( x ) 在区间 ( -∞ , - 1] 上是减函数的问题转换成与概率的基本事件有关的问题 ? 解题心得 1 . 由两个向量的数量积公式 , 得出它们的夹角的余弦值的表达式 , 由夹角的范围得出点数 m 和 n 的关系 m ≥ n , 然后分别求 m=n 和 m>n 对应的事件个数 , 从而也清楚了基本事件的个数就是点数 m 和 n 组成的点的坐标数 . 2 . 直线与圆有公共点 , 即圆心到直线的距离小于或等于半径 , 由此得出 a ≤ b , 则满足 a ≤ b 的基本事件的个数就能求出来 , 从而转化成与概率的基本事件有关的问题 . 3 .f ( x ) 在区间 ( -∞ , - 1] 上是减函数可转化成开口向上的二次函数 f ( x ) 的图象的对称轴与 x 轴的交点的横坐标大于或等于 - 1, 从而得出 b ≤ a , 从而不难得出 b ≤ a 包含的基本事件数 . 因此也转化成了与概率的基本事件有关的问题 . - 20 - 考点一 考点二 考点三 D - 21 - 考点一 考点二 考点三 解析 : (1) 连续掷两次骰子 , 以先后得到的点数 m , n 为点 P 的坐标 ( m , n ), 基本事件总数 N= 6 × 6 = 36, 点 P 在圆 x 2 +y 2 = 17 内部 ( 不包括边界 ) 包含的基本事件有 :(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2), 共 8 个 , - 22 - 考点一 考点二 考点三 (3) 易得 A= { x|- 2 35, 所以去年该居民区 PM2 . 5 年平均浓度不符合《环境空气质量标准》 , 故该居民区的环境需要改善 . - 27 - 考点一 考点二 考点三 思考 如何求解概率与统计相综合的题目 ? 解题心得 有关古典概型与统计综合的题型 , 无论是直接描述还是利用频率分布表、频率分布直方图、茎叶图等给出信息 , 只需要能够从题中提炼出需要的信息 , 此类问题即可解决 . - 28 - 考点一 考点二 考点三 对点训练 3 (2017 河南南阳一模 , 文 18) 已知国家某 5A 级大型景区对拥挤等级与每日游客数量 n ( 单位 : 百人 ) 的关系有如下规定 : 当 n ∈ [0,100) 时 , 拥挤等级为 “ 优 ”; 当 n ∈ [100,200) 时 , 拥挤等级为 “ 良 ”; 当 n ∈ [200,300) 时 , 拥挤等级为 “ 拥挤 ”; 当 n ≥ 300 时 , 拥挤等级为 “ 严重拥挤 ” . 该景区对 6 月份的游客数量作出如图的统计数据 : - 29 - 考点一 考点二 考点三 (1) 下面是根据统计数据得到的频率分布表 , 求出 a , b 的值 , 并估计该景区 6 月份游客人数的平均值 ( 同一组中的数据用该组区间的中点值作代表 ); (2) 某人选择在 6 月 1 日至 6 月 5 日这 5 天中任选 2 天到该景区游玩 , 求他这两天遇到的游客拥挤等级均为 “ 优 ” 的概率 . - 30 - 考点一 考点二 考点三 - 31 - 考点一 考点二 考点三 1 . 古典概型计算三步曲 : 第一 , 试验中每个基本事件必须是等可能的 ; 第二 , 试验的基本事件总共有多少个 ; 第三 , 所求的事件是什么 , 它包含的基本事件有多少个 . 2 . 较复杂事件的概率可灵活运用互斥事件、对立事件的概率公式简化运算 . 3 . 解决与古典概型交汇命题的问题时 , 把相关的知识转化为事件 , 列举基本事件 , 求出基本事件和随机事件的个数 , 然后利用古典概型的概率计算公式进行计算 . - 32 - 考点一 考点二 考点三 古典概型的条件是事件发生的等可能性 , 一定要注意在计算基本事件总数和事件包括的基本事件个数时 , 它们是不是等可能的 .