2018-2019学年四川省成都外国语学校高一下学期期中考试 数学试卷(理)

2018-2019学年四川省成都外国语学校高一下学期期中考试 数学试卷(理)

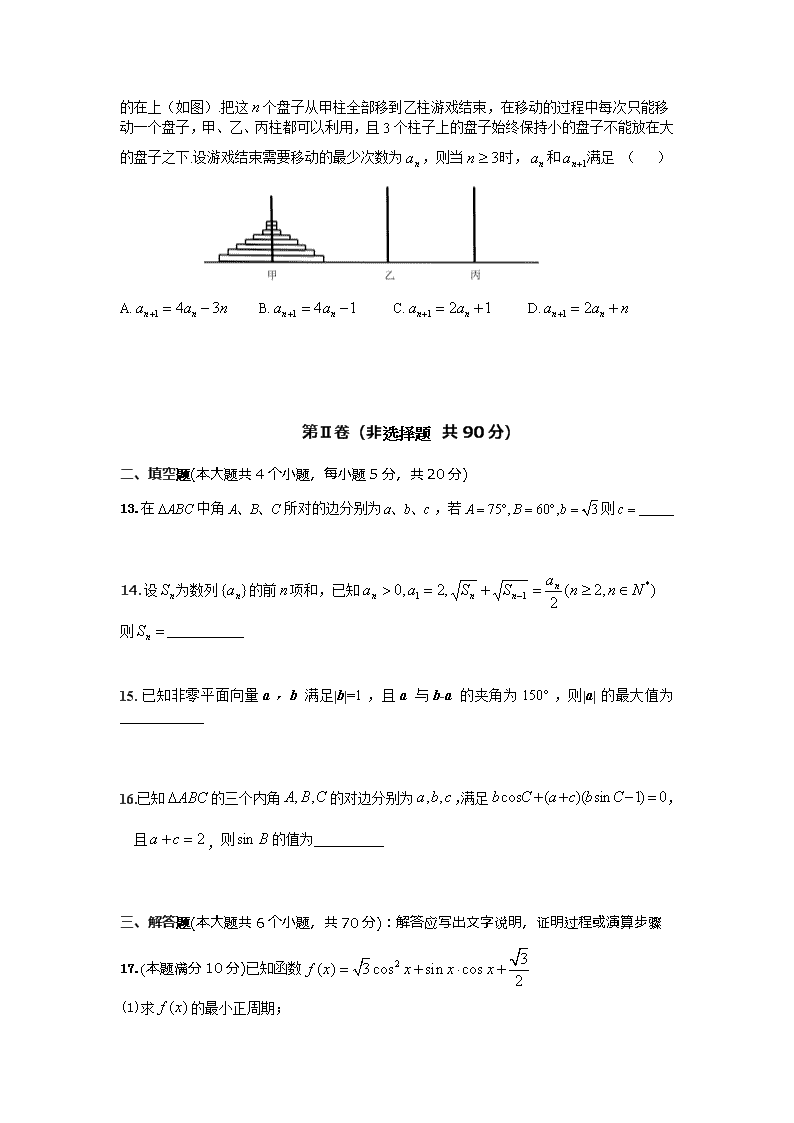
‎2018-2019学年四川省成都外国语学校高一下学期期中考试 数学试卷(理)‎ 注意事项：‎ 1、 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分 2、 本堂考试时间120分钟，满分150分 3、 答题前，请考生务必先将自己的姓名、考号填写在答题卷上，并用2B铅笔填涂 4、 考试结束后，请考生将答题卷交回 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的，并将正确选项的序号填涂在答题卷。‎ ‎1.一个三角形的三个内角的度数成等差数列，则的度数为 （ ）‎ ‎ A. B. C. D. ‎ ‎2.数列，，，，…的一个通项公式是 (　　)‎ A．an＝ B．an＝ C．an＝－ D．an＝1－ ‎3.下面关于等比数列和公比叙述正确的是 （ 　）‎ A.为递增数列 B.为递增函数 C.为递减数列 D.为递增函数列且为递增函数 ‎4.在△ABC中角所对的边分别为以下叙述或变形中错误的是 (　　)‎ A．，a∶b∶c＝sinA∶sinB∶sinC B．a＝b⇔sin2A＝sin2B C．＝ D．‎ ‎5.在△ABC中，若2cosBsinA＝sinC，则△ABC的形状一定是 (　　)‎ A．等腰直角三角形 B．直角三角形 C．等腰三角形 D．等边三角形 ‎6.已知α、β为锐角，cosα＝，tan(α−β)＝−，则tanβ＝ (　　)‎ A、 B、3 C、 D、‎ ‎7.设是等差数列，Sn是其前n项的和，且S5＜S6，S6＝S7＞S8，则下列结论错误的是 （ ）‎ A．d＜0 B．a7＝0 C．S9＞S5 D．S6与S7均为Sn的最大值 ‎8.在中，已知则此三角形有几个解 ( ) ‎ ‎ A．0 B．1 C．2 D．不确定 ‎ ‎9.在中，角、、所对的边分别为、、，若，且，则下列关系一定不成立的是 （ ）‎ A． B． C． D．‎ ‎10.已知 ，且 ，则 （ ）‎ ‎ 　A． B． C． D． ‎ ‎11.某学生家长为缴纳该学生上大学时的教育费，于2018年8月20号从银行贷款a元，为还清这笔贷款，该家长从2019年起每年的8月20号便去银行偿还相同的金额，计划恰好在贷款的m年后还清，若银行按年利率为p的复利计息（复利：即将一年后的贷款利息也纳入本金计算新的利息），则该学生家长每年的偿还金额是 （ ）‎ ‎ A． B．‎ ‎ C． D．‎ ‎ ‎ ‎12.两位同学课余玩一种类似于古代印度的“梵塔游戏”：有3个柱子甲、乙、丙，甲柱上有个盘子，最上面的两个盘子大小相同，从第二个盘子往下大小不等，大的在下，小的在上（如图）.把这个盘子从甲柱全部移到乙柱游戏结束，在移动的过程中每次只能移动一个盘子，甲、乙、丙柱都可以利用，且3个柱子上的盘子始终保持小的盘子不能放在大的盘子之下.设游戏结束需要移动的最少次数为，则当时，和满足 （ ）‎ A. B. C. D.‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题(本大题共4个小题，每小题5分，共20分)‎ ‎13.在中角所对的边分别为，若则 ‎ ‎14.设为数列的前项和，已知 则___________‎ ‎15.已知非零平面向量a，b满足|b|=1，且a与b-a的夹角为150°，则|a|的最大值为____________‎ ‎16.已知的三个内角的对边分别为，满足，且，则的值为__________‎ 三、解答题(本大题共6个小题，共70分)：解答应写出文字说明，证明过程或演算步骤 ‎17.(本题满分10分)已知函数 ‎(1)求的最小正周期；‎ ‎(2)求在区间上的最大值和最小值．‎ ‎18．(本题满分12分)已知sin α＋cos α＝，，，‎ ‎(1)求sin2α和tan2α的值；‎ ‎(2)求cos(α＋2β)的值．‎ ‎19.设正项等比数列中，，且的等差中项为.‎ ‎（1）求数列的通项公式；‎ ‎（2）若，数列的前项和为，数列满足，记为数列的前项和，求.‎ ‎20.(本题满分12分)已知各项均为正数的等差数列的前三项的和为27，且满足，数列的前项和为，且对一切正整数，点都在函数的图象上.‎ ‎(I)求数列和的通项公式；‎ ‎(II)设，求数列的前项和为；‎ ‎21.(本题满分12分)数列的前项和为 ‎（1）若为等差数列，求证：；‎ ‎（2）若，求证：为等差数列.‎ ‎22.(本题满分12分)在中，是的内角，向量，且 ‎（I）求角；（II）求的面积.‎ 成都外国语学校2018－2019学年度下期期中考试 高一数学试卷(理)参考答案 一、选择题：CCDBC BCBBC DC 二、填空题13.；14.；15.2；16.‎ 三、解答题(本大题共6个小题，共70分)：解答应写出文字说明，证明过程或演算步骤 ‎17.(本题满分10分)已知函数 ‎(1)求的最小正周期；(2)求在区间上的最大值和最小值．‎ ‎【解析】（1）‎ ‎…………………………………2分 ‎……………………………………………………4分 所以函数的最小正周期…………………………………………5分 ‎（2）因为，所以………………………………6分 当时，即是………………………………8分 当时，即是………………………………10分 ‎18．(本题满分12分)已知sin α＋cos α＝，，，‎ ‎(1)求sin2α和tan2α的值；(2)求cos(α＋2β)的值．‎ ‎【解析】(1)由题意得(sin α＋cos α)2＝，即1＋sin 2α＝，∴sin2α＝.……3分 又2α∈，∴cos 2α＝＝ ‎∴tan 2α＝＝.…………………………………………6分 ‎(2)∵，‎ 又∴，‎ 于是 又，∴cos 2β＝－，‎ 又∵，∴sin 2β＝………………………………9分 又∵cos2α＝=‎ 又，∴cos α＝，sin α＝.……………………11分 ‎∴cos(α＋2β)＝cosαcos2β－sin α sin2β＝×－×＝－……12分 ‎19.(本题满分12分)设正项等比数列中，，且的等差中项为.‎ ‎（1）求数列的通项公式；（2）若，数列的前项和为，数列满足，记为数列的前项和，求.‎ ‎【解析】（1）设正项等比数列的公比为 由的等差中项为可得………………3分 即则 所以…………………………………………6分 ‎（2）……………………………………7分 则数列是以1为首项，2为公比的等差数列 于是…………………………………………8分 从而…………………………………10分 则 则…………………………………………………………………………12分 ‎20.(本题满分12分)已知各项均为正数的等差数列的前三项的和为27，且满足，数列的前项和为，且对一切正整数，点都在函数的图象上.‎ ‎(I)求数列和的通项公式；(II)设，求数列的前项和为；‎ ‎【解析】（1）设等差数列的公差为，且 由题则 又 则，所以…………………………………………………………3分 又……①‎ 当时……②‎ 由有 当时也满足上式 所以…………………………………………………………………………6分 ‎（2）‎ ‎……③‎ ‎……④………………………………8分 由③-④有 则…………………………10分 ‎…………………………………………………………12分 ‎21.(本题满分12分)数列的前项和为.（1）若为等差数列，求证：；（2）若，求证：为等差数列.‎ ‎【解析】（1）证明：已知)数列为等差数列，设其公差为，有 则 于是……①‎ 又……②‎ 由①②相加有即…………………………6分 ‎（2）证明：由，有当时，，‎ 所以，　　③…………9分 ‎， ④‎ ‎④－③并整理，得，即……11分 所以数列是等差数列．…………………………………………12分 ‎22.(本题满分12分)在中，是的内角，向量，且（I）求角；（II）求的面积.‎ ‎【解析】（I）‎ 又中……………………3分 所以，有，所以…………………………………………6分 ‎（II）在中，设角、、所对的边分别为、、‎ ‎…………………………………………………………7分 又 由余弦定理有………………………………9分 所以代入中有 联立解得 所以……………………………………………………12分