数学理卷·20178届湖南省永州市第四中学高二上学期期末考试（2017-01）

数学理卷·20178届湖南省永州市第四中学高二上学期期末考试（2017-01）

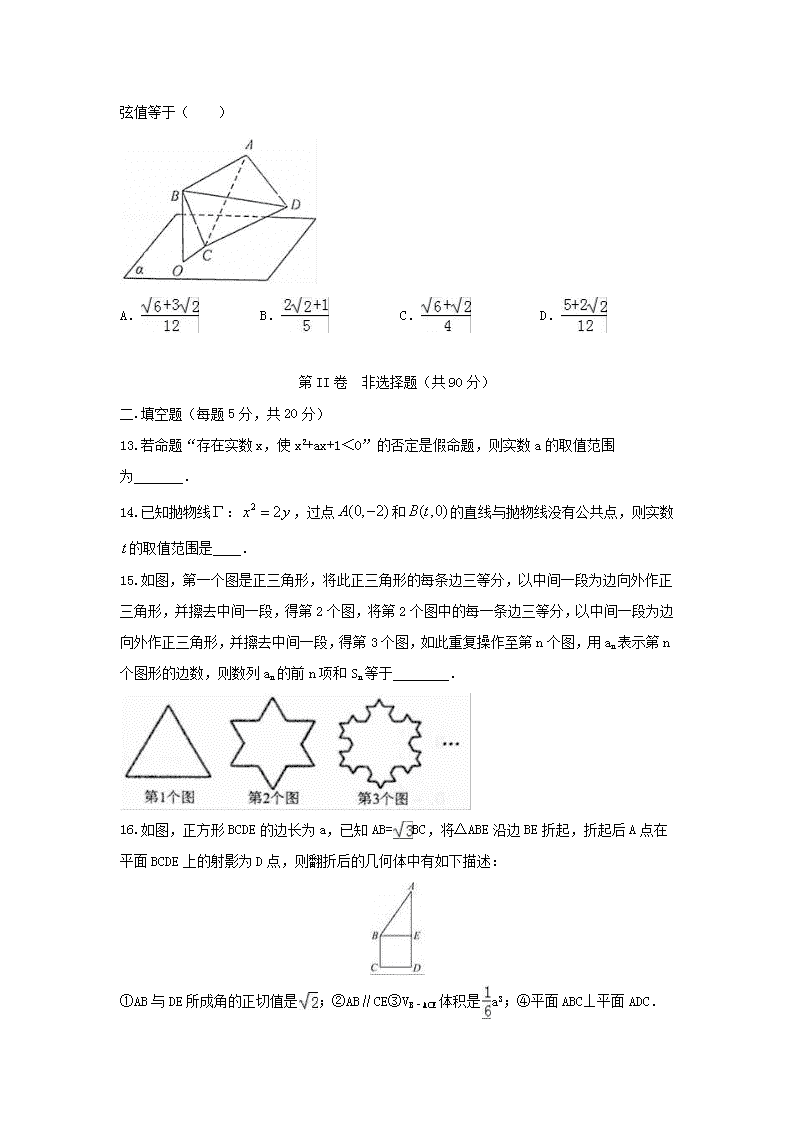
‎ 2016年下期永州市第四中学期末综合质量检测 理科数学（试题卷）‎ 注意事项：‎ ‎1.本卷共22题，满分150分，考试时间为120分钟。请考生注意考试时间，开考15分钟后，考生禁止进入考室，监考老师回收试卷。‎ ‎2.请考生遵守考室秩序，发卷后注意检查试卷是否完整，如果妨碍答题现象请立即通知监考老师。‎ 第I卷 选择题（每题5分，共60分）‎ ‎1.已知a，b∈R，则命题“若a2+b2=0，则a=0或b=0”的否命题是（　　） ‎ A．若a2+b2≠0，则a≠0且b≠0 B．若a2+b2≠0，则a≠0或b≠0 ‎ C．若a≠0且b≠0，则a2+b2≠0 D．若a≠0或b≠0，则a2+b2≠0 ‎ ‎2.双曲线的焦距为（　 ）‎ A. B. C. D. ‎ ‎3.下列求导运算正确的是（　　） ‎ A．（x）′=1 B．（x2cosx）′=﹣2xsinx C．（3x）′=3xlog3e D．（log2x）′= ‎ ‎4.在复平面内，复数i（2﹣i）对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎5.若曲线处的切线与两坐标轴围成的三角形的面积为9，则a=（ ）‎ A．8 B．16 C．32 D．64‎ ‎6.某产品的广告费用x与销售额y的统计数据如下表 根据上表可得回归方程中的为9．4，据此模型预报广告费用为6万元时销售额为（ ）‎ A．63．6万元 B．65．5万元 C．67．7万元 D．72．0万元 ‎7.某校在暑假组织社会实践活动，将8名高一年级学生，平均分配甲、乙两家公司，其中两名英语成绩优秀学生不能分给同一个公司；另三名电脑特长学生也不能分给同一个公司，则不同的分配方案有（ 　）‎ A．36种 B．38种 C．108种 D．114种 ‎8.空间四边形ABCD中，AB=CD，边AB．CD所在直线所成的角为30°，E、F分别为边BC、AD的中点，则直线EF与AB所成的角为（　　）‎ A．75° B．15° C．75°或15° D．90°‎ ‎9.已知F1、F2分别是双曲线﹣=1（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）‎ A．（1，） B．（，+∞） C．（，2） D．（2，+∞）‎ ‎10.如果函数满足：对于任意的，都有恒成立，‎ 则的取值范围是（ ）‎ A． B． C． D．‎ ‎11.如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1，CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（　　）‎ A． B． C． D．‎ ‎12.‎ 如图，正四面体ABCD的顶点C在平面α内，且直线BC与平面α所成角为45°，顶点B在平面α上的射影为点O，当顶点A与点O的距离最大时，直线CD与平面α所成角的正弦值等于（　　）‎ A． B． C． D．‎ 第II卷 非选择题（共90分）‎ 二.填空题（每题5分，共20分）‎ ‎13.若命题“存在实数x，使x2+ax+1＜0”的否定是假命题，则实数a的取值范围为　 　．‎ ‎14.已知抛物线：，过点和的直线与抛物线没有公共点，则实数的取值范围是 ．‎ ‎15.如图，第一个图是正三角形，将此正三角形的每条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第2个图，将第2个图中的每一条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第3个图，如此重复操作至第n个图，用an表示第n个图形的边数，则数列an的前n项和Sn等于　 　．‎ ‎16.如图，正方形BCDE的边长为a，已知AB=BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：‎ ‎①AB与DE所成角的正切值是；②AB∥CE③VB﹣ACE体积是a3；④平面ABC⊥平面ADC．‎ 其中正确的有　　．（填写你认为正确的序号）‎ 三.解答题（请写出对应的文字说明，公式定理，解答过程，共6题，共70分）‎ ‎17.（本题满分10分）‎ 已知命题p：∃x0∈，满足x02+x0﹣a+1＞0，命题q：∀t∈（0，1），方程x2+=1都表示焦点在y轴上的椭圆．若命题p∨q为真命题，p∧q为假命题，求实数a的取值范围．‎ ‎18.（本题满分12分）‎ 如图，已知平面平面，与分别是棱长为1与 ‎2的正三角形，//，四边形为直角梯形，//，，点为的重心，为中点，．‎ ‎（Ⅰ）当时，求证：//平面；‎ ‎（Ⅱ）若直线与所成角为，试求二面角的余弦值．‎ ‎19.（本题满分12分）‎ 某市为了了解高二学生物理学习情况，在34所高中里选出5所学校，随机抽取了近千名学生参加物理考试，将所得数据整理后，绘制出频率分布直方图如图所示. ‎ ‎（1）将34所高中随机编号为01，02，…，34，用下面的随机数表选取5组数抽取参加考试的五所学校.选取方法是从随机数表第一行的第6列和第7列数字开始，由左到右依次取两个数字，则选出来的第4所学校的编号是多少？‎ ‎49 54 43 54 82 17 37 93 23 78 87 35 20‎ ‎96 43 84 26 34 91 64 57 24 55 06 88 77‎ ‎04 74 47 67 21 76 33 50 25 83 92 12 06‎ ‎（2）求频率分布直方图中的值，试估计全市学生参加物理考试的平均成绩；‎ ‎（3）如果从参加本次考试的同学中随机选取3名同学，这3名同学中考试成绩在80分以上（含80分）的人数记为，求的分布列及数学期望.‎ ‎（注：频率可以视为相应的概率）‎ ‎20.（本题满分12分）‎ 如图，在平面直角坐标系xOy中，椭圆C：的左焦点为F，右顶点为A，动点M为右准线上一点（异于右准线与x轴的交点），设线段FM交椭圆C于点P，已知椭圆C的离心率为，点M的横坐标为．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）若∠FPA为直角，求P点坐标；‎ ‎（3）设直线PA的斜率为k1，直线MA的斜率为k2，求k1•k2的取值范围．‎ ‎21. (本题满分12分)‎ ‎ 某旅游景区的观景台P位于高为的山峰上(即山顶到山脚水平面M的垂直高度)，山脚下有一段位于水平线上笔直的公路AB，山坡面可近似地看作平面PAB，且为以为底边的等腰三角形. 山坡面与山脚所在水平面M所成的二面角为，且. 现从山脚的水平公路AB某处C0开始修建一条盘山公路，该公路的第一段, 第二段, 第三段, …, 第n－1段依次为C0C1，C1C2，C2C3，…，Cn－1Cn(如图所示)，C0C1，C1C2，C2C3，…，Cn－1Cn与AB所成的角均为，且.‎ ‎（1）问每修建盘山公路多少米，垂直高度就能升高100米? 若修建盘山公路至半山腰(高度为山高的一半)，在半山腰的中心Q处修建上山缆车索道站，索道PQ依山而建(与山坡面平行，离坡面高度忽略不计)，问盘山公路的长度和索道的长度各是多少？‎ ‎（2）若修建盘山公路，其造价为万元. 修建索道的造价为万元. 问修建盘山公路至多高时，再修建上山索道至观景台，总造价最少?‎ ‎22.（本题满分12分）‎ 已知函数f（x）=lnx．‎ ‎（1）求函数g（x）=f（x+1）﹣x的最大值；‎ ‎（2）若对任意x＞0，不等式f（x）≤ax≤x2+1恒成立，求实数a的取值范围；‎ ‎（3）若x1＞x2＞0，求证：＞．‎ ‎2016年下期永州四中高二年级期末考试理科数学参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B D A B B A C D C A A ‎ ‎ ‎13.a＜﹣2或a＞2‎ ‎14.‎ ‎15.4n﹣1‎ ‎16.①③④‎ ‎17.‎ 因为∃x0∈，满足，所以只须；‎ ‎∵，∴x0=1时，的最大值为3﹣a，∴3﹣a＞0，所以命题p：a＜3；‎ 因为∀t∈（0，1），方程都表示焦点在y轴上的椭圆，所以t2﹣（2a+2）t+a2+2a+1＞1即t2﹣（2a+2）t+a2+2a=（t﹣a）（t﹣（a+2））＞0对t∈（0，1）恒成立，只须a+2≤0或a≥1，得a≤﹣2或a≥1；‎ 根据已知条件知，p和q中一真一假：‎ 若p真q假，得，即﹣2＜a＜1；‎ 若p假q真，得，得a≥3‎ 综上所述，﹣2＜a＜1，或a≥3；‎ ‎∴a的取值范围为（﹣2，1）∪．‎ ‎（3）当x1＞x2＞0时，＞等价于．‎ 令t=，设u（t）=lnt﹣，t＞1‎ 则＞0，‎ ‎∴u（t）在（1，+∞）上单调递增，‎ ‎∴u（t）＞u（1）=0，‎ ‎∴＞．‎ ‎ ‎