- 2021-07-01 发布 |
- 37.5 KB |
- 10页

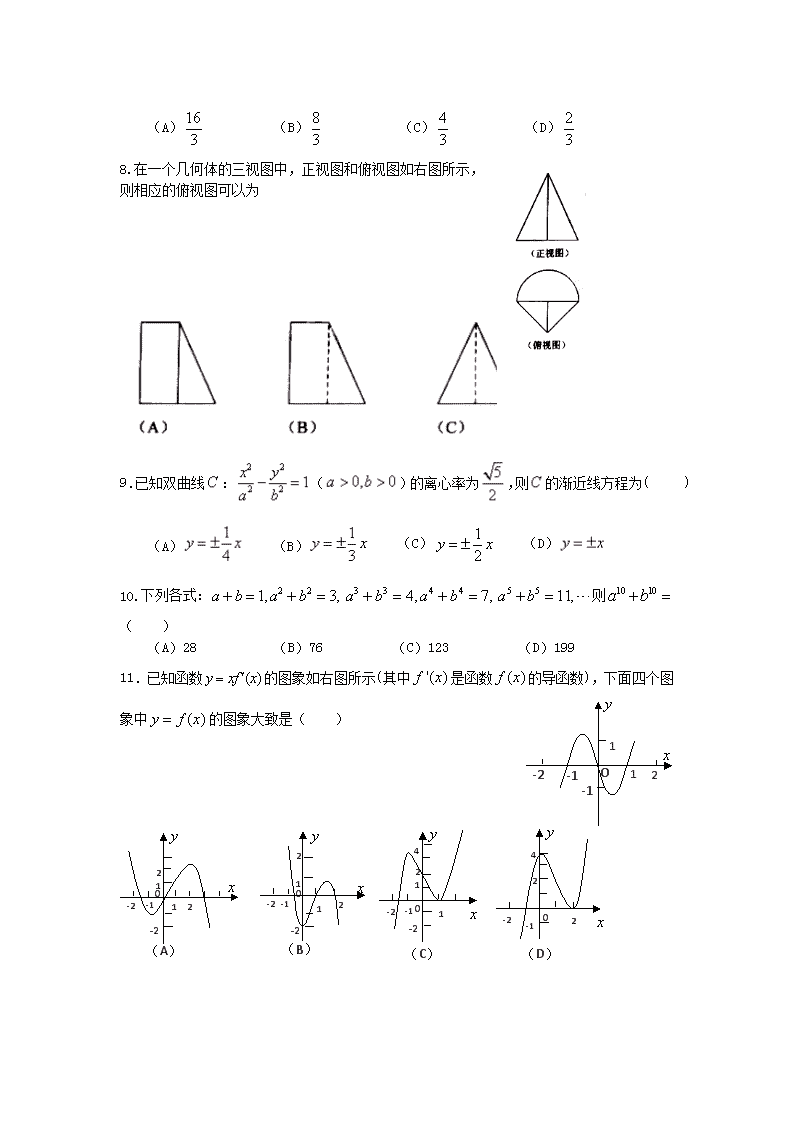

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届广东省仲元中学高二下学期期中考试(2017-04)
广东仲元中学2016学年第二学期期中考试 高二年级理科数学学科试卷 命题人: 审题人: 一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。 1.复数的实部是( ) (A) (B) (C)3 (D) 2. 函数,已知在时取得极值,则=( ) (A)2 (B) 3 (C) 4 (D)5 3.用反证法证明命题:“已知为实数,则方程至少有一个实根”时,要做的假设是 (A)方程没有实根 (B)方程至多有一个实根 (C)方程至多有两个实根(D)方程恰好有两个实根 4. 函数的定义域为 (A) (B) (C) (D) 5.设D为△ABC所在平面内一点,则 (A) (B) (C) (D) 6.的展开式中的系数( ) (A)-56 (B)56 (C)-336 (D)336 7.如下图,已知幂函数的图像过点,则图中阴影部分的面积等于( ) (A) (B) (C) (D) 8.在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的俯视图可以为 9.已知双曲线:()的离心率为,则的渐近线方程为( ) (A) (B) (C) (D) 10.下列各式:则( ) (A)28 (B)76 (C)123 (D)199 -2 2 O 1 -1 -1 1 11.已知函数的图象如右图所示(其中是函数的导函数),下面四个图象中的图象大致是( ) O -2 2 1 -1 -2 1 2 O -2 -2 2 1 -1 1 2 O -2 4 1 -1 -2 1 2 O -2 2 -1 2 4 (A) (B) (C) (D) 12.是定义在上单调递减的奇函数,当时,的取值范围是 ( ) (A) (B) (C) (D) 二、填空题:本大题共4小题,每小题5分 13.如果曲线与在处的切线互相垂直,则= . 14.把编号为1,2,3,4的四封电子邮件分别发送到编号为1,2,3,4的四个网址,则至多有一封邮件的编号与网址的编号相同的概率为 . 15.已知正弦函数具有如下性质: 若,则(其中当时等号成立).根据上述结论可知,在中,的最大值为__ __. 16. 下列几个命题: ①方程有一个正实根,一个负实根,则; ② 和表示相同函数; ③ 函数是非奇非偶函数; ④方程有两解,则 其中正确的有___________________. 三、解答题(6题,共70分,要求写出解答过程或者推理步骤) 17.(本题满分1 0分)已知函数的图象在 轴右侧的第一个最高点和第一个最低点的坐标分别为和. (1)求函数的解析式; (2)求的值 18.(本题满分1 2分)2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示: 等 级 一级 二级 三级 四级 频 率 0.30 0.10 现从该港口随机抽取了家公司,其中消防安全等级为三级的恰有20家. (Ⅰ)求的值; (Ⅱ)按消防安全等级利用分层抽样的方法从这家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率. 19.(本题满分12分) 设等差数列的公差为d,前项和为,等比数列的公比为.已知,,,. (Ⅰ)求数列,的通项公式; (Ⅱ)当时,记,求数列的前项和. 20. (本题满分1 2分)如图,在四棱锥中,底面是平行四边形,,侧面底面,,, 分别为的中点,点在线段上. (Ⅰ)求证:平面; (Ⅱ)如果直线与平面所成的角和直线与平面所成的角相等,求的值. 21. (本题满分1 2分)已知椭圆:()的焦距为,且经过点. (Ⅰ)求椭圆的方程; (Ⅱ)、是椭圆上两点,线段的垂直平分线经过,求面积的最大值(为坐标原点). 22. (本题满分1 2分)已知函数. (Ⅰ)当时,求函数的图象在点(1,)处的切线方程; (Ⅱ)讨论函数的单调区间; (Ⅲ)已知,对于函数图象上任意不同的两点,其中,直线的斜率为,记,若求证 广东仲元中学2016学年第二学期期中考试高二年级理科数学学科试卷(答案) 一、 选择: 1-5:B、D、A、C、A 6-:10:A、B、D、C 、C 11-12:C、D. 二、填空: 13. 14. 15. 16.___①④____. 三、解答: 17. 解:由题意可得, …………………………1分 , …………………………3分 ∴ …………………………4分 由得, …………………………5分 ∴. …………………………6分 (2)解: ∵ 点是函数在轴右侧的第一个最高点, ∴ . …………………………7分 ∴ . …………………………8分 ∴ …………………………9分 . …………………………10分 18解: (Ⅰ)由已知可得;0.30+2m+m+0.10=1,解得:m=0.20. ……………………2分 所以. ……………………4分 (Ⅱ)由(Ⅰ)知,利用分层抽样的方法从中抽取10家公司,则消防安全等级为一级的有3家,二级的有4家,三级的有2家,四级的有1家. ……………………6分 记消防安全等级为二级的4家公司分别为A,B,C,D,三级的2家公司分别记为,,则从中抽取2家公司,不同的结果为(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)(A,)(A,)(B,)(B,)(C,)(C,)(D,)(D,)(,)…共15种,………8分 记“抽取的2家公司的消防安全等级都是二级”为事件M,则事件M包含的结果有:(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)…共6种,……………………10分 所以. ……………………12分 19. 解:(1)由题意有, 即 ……………………2分 解得或 ……………………4分 故或……………………6分 (2)由d>1,知an=2n-1,bn=2n-1,故cn=,于是Tn=1+++++…+, ①……………………8分 Tn=+++++…+. ②……………………10分 ①-②可得 Tn=2+++…+-=3-, 故Tn=6-.……………………12分 20. (Ⅰ)证明:在平行四边形中,因为,, 所以.由分别为的中点,得, 所以. …………2分 因为侧面底面,且,所以底面. 又因为底面,所以. …………4分 又因为,平面,平面, 所以平面. ………………6分 (Ⅱ)解:因为底面,,所以两两垂直,以分别为、、,建立空间直角坐标系, 则, 所以,,,设, 则, 所以, ,易得平面的法向 量. 设平面的法向量为,由,,得 令, 得. 因为直线与平面所成的角和此直线与平面所成的角相等, 所以,即, 所以 , 解得,或(舍). 综上所得:……12分 21. 解:(Ⅰ)依题意,,椭圆的焦点为,……1分 ……3分 所以,椭圆的方程为……4分 (Ⅱ)根据椭圆的对称性,直线与轴不垂直,设直线:……5分 由得,……6分 设,,则,……7分 ,到直线的距离,的面积……8分 依题意,,, ……9分 ,,代入整理得,……10分 若,则,等号当且仅当时成立……11分 若,则,,等号当且仅当, 时成立。 综上所述,面积的最大值为……12分 22. 解:(Ⅰ)当时, 1分 又2分 函数的图象在点(1,)处的切线方程为:, 即3分 (Ⅱ)的定义域为 4分 当时,在上恒成立,在定义域内单调递增; 5分 当时,令解得, 则时,,单调递增; 时,,单调递减;6分 综上,时,的单调递增区间为; 时,的单调递增区间为, 的单调递增区间为 …….7分 (Ⅲ)证明: , 又, …….8分 要证:,只需证 …….9分 即证:,设 令则 …….10分 令 对称轴. …….11分 ,故在内单调递减,则; 故. …….12分查看更多