数学理卷·2017届北京昌平临川育人学校高三上学期期末考试（2017

数学理卷·2017届北京昌平临川育人学校高三上学期期末考试（2017

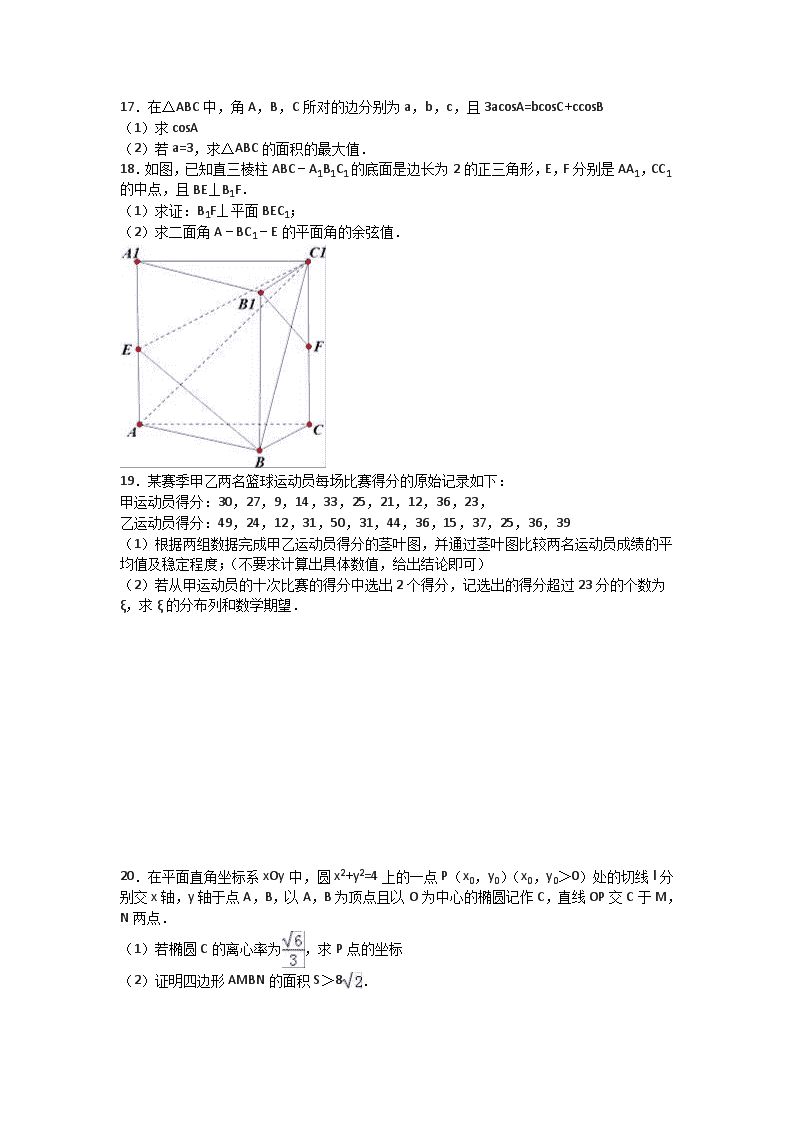
北京临川育人学校2016—2017学年上学期期末考试 高三理科数学试卷 ‎ 命题 ——李永刚 一、选择题 ‎1．设集合A={x|x2﹣3x＞0}，B={x||x|＜2}，则A∩B=（　　）‎ A．（﹣2，0） B．（﹣2，3） C．（0，2） D．（2，3）‎ ‎2．把复数z的共轭复数记作，已知（3﹣4i）=1+2i，则z=（　　）‎ A． +i B．﹣+i C．﹣﹣i D．﹣‎ ‎3．设命题p：∀x＞0，x＞lnx．则￢p为（　　）‎ A．∀x＞0，x≤lnx B．∀x＞0，x＜lnx C．∃x0＞0，x0＞lnx0 D．∃x0＞0，x0≤lnx0【来源：全,品…中&高*考+网】‎ ‎4．已知向量、，其中||=，||=2，且（﹣）⊥，则向量和的夹角是（　　）‎ A． B． C． D．π ‎5．如图，网格纸上小正方形的边长为1，粗线画出的为某几何体的三视图，则此几何体的体积为（　　）‎ A． B．1 C． D．2‎ ‎6．已知2sin2α=1+cos2α，则tan（α+）的值为（　　）‎ A．﹣3 B．3 C．﹣3或3 D．﹣1或3‎ ‎7．执行如图所示的程序框图，则输出的c的值是（　　）‎ A．8 B．13 C．21 D．34‎ ‎8．如图，在多面体ABC﹣DEFG中，平面ABC∥平面DEFG，AC∥GF，且△ABC是边长为2的正三角形，DEFG是边长为4的正方形，M，N分别是AD，BE的中点，则MN=（　　）‎ A． B．4 C． D．5‎ ‎9．已知f（x）=asinx+cosx，若f（+x）=f（﹣x），则f（x）的最大值为（　　）‎ A．1 B． C．2 D．2‎ ‎10．设数列{an}的前n项和为Sn，若Sn+1，Sn，Sn+2成等差数列，且a2=﹣2，则a7=（　　）‎ A．16 B．32 C．64 D．128‎ ‎11．设双曲线=1的两焦点分别为F1，F2，P为双曲线上的一点，若PF1与双曲线的一条渐近线平行，则•=（　　）‎ A． B． C． D．‎ ‎12．已知f′（x）是函数f（x），（x∈R）的导数，满足f′（x）=﹣f（x），且f（0）=2，设函数g（x）=f（x）﹣lnf3（x）的一个零点为x0，则以下正确的是（　　）‎ A．x0∈（﹣4，﹣3） B．x0∈（﹣3，﹣2） C．x0∈（﹣2，﹣1） D．x0∈（﹣1，0）‎ ‎　‎ 二、填空题 ‎13．已知实数x，y满足，若x﹣y的最大值为6，则实数m=　　　　　　．‎ ‎14．二项式（﹣）n的展开式中各项系数之和为，则展开式中的常数项为　　　　　　．‎ ‎15．已知{an}是公差不为0的等差数列，{bn}为等比数列，满足a1=3，b1=1，a2=b2，3a5=b3，若对于每一个正整数n，均有an=a1+logabn，则常数a=　　　　　　．‎ ‎16．已知△ABC的三个顶点均在抛物线y2=x上，边AC的中线BM∥x轴，|BM|=2，则△ABC的面积为　　　　　　．‎ ‎　‎ 三、解答题 ‎17．在△ABC中，角A，B，C所对的边分别为a，b，c，且3acosA=bcosC+ccosB ‎（1）求cosA ‎（2）若a=3，求△ABC的面积的最大值．‎ ‎18．如图，已知直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是AA1，CC1的中点，且BE⊥B1F．‎ ‎（1）求证：B1F⊥平面BEC1；‎ ‎（2）求二面角A﹣BC1﹣E的平面角的余弦值．‎ ‎19．某赛季甲乙两名篮球运动员每场比赛得分的原始记录如下：‎ 甲运动员得分：30，27，9，14，33，25，21，12，36，23，‎ 乙运动员得分：49，24，12，31，50，31，44，36，15，37，25，36，39‎ ‎（1）根据两组数据完成甲乙运动员得分的茎叶图，并通过茎叶图比较两名运动员成绩的平均值及稳定程度；（不要求计算出具体数值，给出结论即可）‎ ‎（2）若从甲运动员的十次比赛的得分中选出2个得分，记选出的得分超过23分的个数为ξ，求ξ的分布列和数学期望．‎ ‎20．在平面直角坐标系xOy中，圆x2+y2=4上的一点P（x0，y0）（x0，y0＞0）处的切线l分别交x轴，y轴于点A，B，以A，B为顶点且以O为中心的椭圆记作C，直线OP交C于M，N两点．‎ ‎（1）若椭圆C的离心率为，求P点的坐标 ‎（2）证明四边形AMBN的面积S＞8．‎ ‎21．已知函数f（x）=aex+bxlnx图象上x=1处的切线方程为y=2ex﹣e．‎ ‎（Ⅰ）求实数a和b的值；‎ ‎（Ⅱ）求函数g（x）=f（x）﹣ex2的最小值．‎ ‎　‎ 选考题（二选一）[选修4-1：几何证明选讲]‎ ‎ [选修4-4：坐标系与参数方程]‎ ‎23．在平面直角坐标系xoy中，直线，（t为参数）与抛物线y2=2px（p＞0）相交于横坐标分别为x1，x2的A，B两点 ‎（1）求证：x02=x1x2；‎ ‎（2）若OA⊥OB，求x0的值．‎ ‎　‎ ‎[选修4-5：不等式选讲]024．已知a，b∈R+，设x=，y=，求证：‎ ‎（1）xy≥ab；‎ ‎（2）x+y≤a+b．‎ ‎　‎ 北京临川育人学校2016—2017学年上学期期末考试高三理科数学答案 ‎ 命题 ——李永刚 一、选择题 ‎1．设集合A={x|x2﹣3x＞0}，B={x||x|＜2}，则A∩B=（　　）‎ A．（﹣2，0） B．（﹣2，3） C．（0，2） D．（2，3）‎ ‎【考点】交集及其运算．‎ ‎【分析】化简集合A、B，再求A∩B．‎ ‎【解答】解：∵集合A={x|x2﹣3x＞0}={x|x＜0或x＞3}=（﹣∞，0）∪（3，+∞），‎ B={x||x|＜2}={x|﹣2＜x＜2}=（﹣2，2），‎ ‎∴A∩B=（﹣2，0）．‎ 故选：A．‎ ‎　‎ ‎2．把复数z的共轭复数记作，已知（3﹣4i）=1+2i，则z=（　　）‎ A． +i B．﹣+i C．﹣﹣i D．﹣‎ ‎【考点】复数代数形式的乘除运算．‎ ‎【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简，求得，则z可求．‎ ‎【解答】解：∵，‎ ‎∴．‎ 故选：C．‎ ‎　‎ ‎3．设命题p：∀x＞0，x＞lnx．则￢p为（　　）‎ A．∀x＞0，x≤lnx B．∀x＞0，x＜lnx C．∃x0＞0，x0＞lnx0 D．∃x0＞0，x0≤lnx0‎ ‎【考点】命题的否定．‎ ‎【分析】根据全称命题的否定是特称命题进行判断．‎ ‎【解答】解；∵命题是全称命题的否定，是特称命题，只否定结论．‎ ‎∴￢p：x0≤lnx0‎ 故选：D．‎ ‎　‎ ‎4．已知向量、，其中||=，||=2，且（﹣）⊥，则向量和的夹角是（　　）‎ A． B． C． D．π ‎【考点】平面向量数量积的运算．‎ ‎【分析】由（﹣）⊥，则（）=0，即有=，再由向量的数量积的定义和性质，即可得到夹角．‎ ‎【解答】解：由于||=，||=2，且（﹣）⊥，‎ 则（）=0，即有=，‎ 则2=×＞，‎ 则有cos＜＞=，‎ 即有向量和的夹角为．【来源：全,品…中&高*考+网】‎ 故选A．‎ ‎　‎ ‎5．如图，网格纸上小正方形的边长为1，粗线画出的为某几何体的三视图，则此几何体的体积为（　　）‎ A． B．1 C． D．2‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】依三视图知该几何体为三棱锥，画出直观图、判断出位置关系和求出长度，利用椎体的体积公式求出答案．‎ ‎【解答】解：依三视图知该几何体为三棱锥P﹣ABC，‎ 且PD⊥平面ABD，AD⊥BD，C是AD的中点，PD=AD=BD=2，‎ 所以其体积，‎ 故选：A．‎ ‎　‎ ‎6．已知2sin2α=1+cos2α，则tan（α+）的值为（　　）‎ A．﹣3 B．3 C．﹣3或3 D．﹣1或3‎ ‎【考点】两角和与差的正切函数．‎ ‎【分析】由倍角公式求得sinα与cosα的数量关系，结合正弦、余弦以及正切函数的转化关系进行解答即可．‎ ‎【解答】解：∵2sin2α=1+cos2α，‎ ‎∴4sinαcosα=1+2cos2α﹣1，‎ 即2sinαcosα=cos2α，‎ ‎①当cosα=0时，，此时，‎ ‎②当cosα≠0时，，此时，‎ 综上所述，tan（α+）的值为﹣1或3．‎ 故选：D．‎ ‎　‎ ‎7．执行如图所示的程序框图，则输出的c的值是（　　）‎ A．8 B．13 C．21 D．34‎ ‎【考点】程序框图．‎ ‎【分析】框图首先给变量a，b，k赋值，a=1，b=1，k=0，然后执行一次运算k=k+1，判断k＜6是否成立，成立则执行用a+b替换c，用b替换a，用c替换b，用k+1替换k，不成立输出c的值，然后再判断k＜6是否成立，依次判断执行．‎ ‎【解答】解：框图首先给变量a，b，k赋值，a=1，b=1，k=0，‎ 执行k=0+1=1；‎ 判断1＜6成立，执行c=1+1=2，a=1，b=2，k=1+1=2；‎ 判断2＜6成立，执行c=1+2=3，a=2，b=3，k=2+1=3；‎ 判断3＜6成立，执行c=2+3=5，a=3，b=5，k=3+1=4；‎ 判断4＜6成立，执行c=3+5=8，a=5，b=8，k=4+1=5；‎ 判断5＜6成立，执行c=5+8=13，a=8，b=13，k=5+1=6；‎ 判断6＜6不成立，跳出循环，输出c=13．‎ 故选B．‎ ‎　‎ ‎8．如图，在多面体ABC﹣DEFG中，平面ABC∥平面DEFG，AC∥GF，且△ABC是边长为2的正三角形，DEFG是边长为4的正方形，M，N分别是AD，BE的中点，则MN=（　　）‎ A． B．4 C． D．5‎ ‎【考点】点、线、面间的距离计算．‎ ‎【分析】取BD中点P，连结MP，NP，利用余弦定理，求出MN．‎ ‎【解答】解：如图，取BD中点P，连结MP，NP，‎ 则MP∥AB，NP∥DE，，，‎ 又∵AC∥GF，∴AC∥NP，∵∠CAB=60°，∴∠MPN=120°，‎ ‎∴．‎ 故选A．‎ ‎　‎ ‎9．已知f（x）=asinx+cosx，若f（+x）=f（﹣x），则f（x）的最大值为（　　）‎ A．1 B． C．2 D．2‎ ‎【考点】三角函数中的恒等变换应用．‎ ‎【分析】由题意得f（x）的对称轴为，及f（x）=sin（x+α），由此得到f（x）的最值的关系式，得到a=1，由此得到f（x）的最大值．‎ ‎【解答】选B．解：由题意得f（x）的对称轴为，‎ f（x）=asinx+cosx=sin（x+α）‎ 当时，f（x）取得最值 即，得a=1，‎ ‎∴f（x）的最大值为．‎ 故选B．‎ ‎　‎ ‎10．设数列{an}的前n项和为Sn，若Sn+1，Sn，Sn+2成等差数列，且a2=﹣2，则a7=（　　）‎ A．16 B．32 C．64 D．128‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】由题意得Sn+2+Sn+1=2Sn，得an+2=﹣2an+1，从而得到{an}从第二项起是公比为﹣2的等比数列，由此能求出结果．‎ ‎【解答】解：∵数列{an}的前n项和为Sn，若Sn+1，Sn，Sn+2成等差数列，且a2=﹣2，‎ ‎∴由题意得Sn+2+Sn+1=2Sn，得an+2+an+1+an+1=0，即an+2=﹣2an+1，‎ ‎∴{an}从第二项起是公比为﹣2的等比数列，‎ ‎∴．‎ 故选：C．‎ ‎　‎ ‎11．设双曲线=1的两焦点分别为F1，F2，P为双曲线上的一点，若PF1与双曲线的一条渐近线平行，则•=（　　）‎ A． B． C． D．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】求得双曲线的a，b，c，可得两焦点的坐标和渐近线方程，可设PF1与直线平行，求得平行线的方程代入双曲线的方程，求得P的坐标，再由向量的数量积的坐标表示，计算即可得到所求值．‎ ‎【解答】解：由双曲线=1的a=，b=1，c=2，‎ 得F1（﹣2，0），F2（2，0），‎ 渐近线为，‎ 由对称性，不妨设PF1与直线平行，‎ 可得，‎ 由得，‎ 即有，，‎ ‎•=﹣×+（﹣）2=﹣．‎ 故选B．‎ ‎　‎ ‎12．已知f′（x）是函数f（x），（x∈R）的导数，满足f′（x）=﹣f（x），且f（0）=2，设函数g（x）=f（x）﹣lnf3（x）的一个零点为x0，则以下正确的是（　　）‎ A．x0∈（﹣4，﹣3） B．x0∈（﹣3，﹣2） C．x0∈（﹣2，﹣1） D．x0∈（﹣1，0）‎ ‎【考点】利用导数研究函数的单调性．‎ ‎【分析】求出f（x）的表达式，得到g（x）的表达式，设h（x）=f（x）﹣g（x），求出h（0）和h（﹣1）的值，从而求出x0的范围．‎ ‎【解答】解：设f（x）=ke﹣x，‎ 则f（x）满足f′（x）=﹣f（x），‎ 而f（0）=2，∴k=2，‎ ‎∴f（x）=2e﹣x，‎ ‎∴g（x）=3lnf（x）=3（﹣x+ln2）=﹣3x+3ln2，‎ 设h（x）=f（x）﹣g（x），‎ 则h（x）=2e﹣x+3x﹣3ln2，‎ ‎∴h（0）=2﹣3ln2＜0，h（﹣1）=2e﹣3﹣3ln2＞0，‎ 即在（﹣1，0）上存在零点，‎ 故选：D．‎ ‎　‎ 二、填空题 ‎13．已知实数x，y满足，若x﹣y的最大值为6，则实数m=　8　．‎ ‎【考点】简单线性规划．‎ ‎【分析】依题意，在平面直角坐标系内画出题中的不等式组表示的平面区域及直线x﹣y=6，结合图形可知，要使直线x﹣y=6经过该平面区域内的点时，其在x轴上的截距达到最大，直线x+y﹣m=0必经过直线x﹣y=6与直线y=1的交点（7，1），于是有7+1﹣m=0，即m=8．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 图形可知，要使直线x﹣y=6经过该平面区域内的点时，其在x轴上的截距达到最大，‎ 直线x+y﹣m=0必经过直线x﹣y=6与直线y=1的交点A（7，1），于是有7+1﹣m=0，即m=8．‎ 故答案为：8．‎ ‎　‎ ‎14．二项式（﹣）n的展开式中各项系数之和为，则展开式中的常数项为　﹣　．‎ ‎【考点】二项式系数的性质．‎ ‎【分析】先x=1，求出n的值，再利用二项式展开式的通项公式求出常数项．‎ ‎【解答】解：令x=1，根据题意有，‎ 解得n=6；‎ ‎（﹣）6展开式的通项公式为：‎ ‎，‎ 令，解得r=3；‎ 所以，展开式的常数项为：‎ ‎．‎ 故答案为：﹣．‎ ‎　‎ ‎15．已知{an}是公差不为0的等差数列，{bn}为等比数列，满足a1=3，b1=1，a2=b2，3a5=b3，若对于每一个正整数n，均有an=a1+logabn，则常数a=　　．‎ ‎【考点】等比数列的通项公式；等差数列的通项公式．‎ ‎【分析】设等差数列{an}的公差为d，等比数列{bn}的公比为q，由题意列式求得d，q的值，则等差数列和等比数列的通项公式可求，代入an=a1+logabn，求解即可得到a值．‎ ‎【解答】解：设等差数列{an}的公差为d，等比数列{bn}的公比为q，‎ ‎∵a1=3，b1=1，a2=b2，3a5=b3，‎ ‎∴，解得d=6，q=9，【来源：全,品…中&高*考+网】‎ ‎∴an=3+6（n﹣1）=6n﹣3，，‎ 代入an=a1+logabn得，‎ ‎，‎ 即loga9=6，‎ ‎∴．‎ 故答案为：．‎ ‎　‎ ‎16．已知△ABC的三个顶点均在抛物线y2=x上，边AC的中线BM∥x轴，|BM|=2，则△ABC的面积为　　．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】作AH⊥BM交BM的延长线于H，求出|BM|，|AH|，即可求得△ABC的面积．‎ ‎【解答】解：根据题意设A（a2，a），B（b2，b），C（c2，c），不妨设a＞c，‎ ‎∵M为边AC的中点，∴，又BM∥x轴，则，‎ 故，‎ ‎∴（a﹣c）2=8，即，‎ 作AH⊥BM交BM的延长线于H．‎ 故．‎ 故答案为：．‎ ‎　‎ 三、解答题 ‎17．在△ABC中，角A，B，C所对的边分别为a，b，c，且3acosA=bcosC+ccosB ‎（1）求cosA ‎（2）若a=3，求△ABC的面积的最大值．‎ ‎【考点】正弦定理；余弦定理．‎ ‎【分析】（1）根据正弦定理将边化角，利用两角和的正弦函数公式化简得出cosA；‎ ‎（2）利用余弦定理和基本不等式得出bc的最大值，代入三角形的面积公式求出面积最大值．‎ ‎【解答】解：（1）在△ABC中，∵3acosA=bcosC+ccosB，‎ ‎∴3sinAcosA=sinBcosC+sinCcosB=sin（B+C）=sinA，即3sinAcosA=sinA，‎ 又A∈（0，π），∴sinA≠0，‎ ‎∴．‎ ‎（2）∵a2=b2+c2﹣2bccosA，即，∴b2+c2=9+bc≥2bc，∴．‎ ‎∵sinA==，‎ ‎∴△ABC的面积，（时取等号）‎ ‎∴．‎ ‎　‎ ‎18．如图，已知直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是AA1，CC1的中点，且BE⊥B1F．‎ ‎（1）求证：B1F⊥平面BEC1；‎ ‎（2）求二面角A﹣BC1﹣E的平面角的余弦值．‎ ‎【考点】二面角的平面角及求法；直线与平面垂直的判定．‎ ‎【分析】（Ⅰ）分别取BC1，BC中点D，G，连结ED，AG，推导出AG⊥面BCC1B1，从而ED⊥B1F，BE⊥B1F，由此能证明B1F⊥面BEC1．‎ ‎（Ⅱ）以O为原点，OE为x轴，OC为y轴，过O作平面ABC的垂线为z轴，建立空间直角坐标系O﹣xyz，利用向量法能求出二面角A﹣BC1﹣E的余弦值．‎ ‎【解答】证明：（Ⅰ）分别取BC1，BC中点D，G，连结ED，AG，‎ ‎∵ABC﹣A1B1C1是直三棱柱，且底面是正三角形，‎ ‎∴AG⊥面BCC1B1，又∵E，D都是中点，‎ 由题意ED∥AG，∴ED⊥面BCC1B1，∴ED⊥B1F，‎ 已知BE⊥B1F，BE∩ED=E，∴B1F⊥面BEC1； …‎ 解：（Ⅱ）由（Ⅰ）知B1F⊥面BEC1，∴B1F⊥BC1，‎ 由题意∽，‎ ‎∴，设BB1=a，则，代入得，‎ 以O为原点，OE为x轴，OC为y轴，过O作平面ABC的垂线为z轴，建立如图坐标系O﹣xyz，‎ 得A（0，﹣1，0），，，‎ ‎，，，‎ 则，，，‎ ‎∵B1F⊥面BEC1，∴平面 BEC1的法向量为==（﹣，1，﹣），‎ 设平面ABC1的法向量为=（x，y，z），‎ 则，得，取x=1，得=（1，﹣，），‎ 设二面角A﹣BC1﹣E的平面角为θ，‎ ‎∴cosθ==，‎ ‎∴二面角A﹣BC1﹣E的余弦值为．…‎ ‎　‎ ‎19．某赛季甲乙两名篮球运动员每场比赛得分的原始记录如下：‎ 甲运动员得分：30，27，9，14，33，25，21，12，36，23，‎ 乙运动员得分：49，24，12，31，50，31，44，36，15，37，25，36，39‎ ‎（1）根据两组数据完成甲乙运动员得分的茎叶图，并通过茎叶图比较两名运动员成绩的平均值及稳定程度；（不要求计算出具体数值，给出结论即可）‎ ‎（2）若从甲运动员的十次比赛的得分中选出2个得分，记选出的得分超过23分的个数为ξ，求ξ的分布列和数学期望．‎ ‎【考点】离散型随机变量的期望与方差；茎叶图；离散型随机变量及其分布列．‎ ‎【分析】（Ⅰ）由某赛季甲乙两名篮球运动员每场比赛得分的原始记录作出茎叶图，由茎叶图得，乙的平均值大于甲的平均数，甲比乙稳定．‎ ‎（Ⅱ）根据题意ξ的所有可能取值为0，1，2，分别求出相应的概率，由此能求出ξ的分布列和数学期望．‎ ‎【解答】‎ 解：（Ⅰ）由某赛季甲乙两名篮球运动员每场比赛得分的原始记录作出茎叶图：‎ 由茎叶图得，乙的平均值大于甲的平均数，甲比乙稳定．…‎ ‎（Ⅱ）根据题意ξ的所有可能取值为0，1，2，‎ 则，‎ ‎，‎ ‎，‎ 所以ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ P（ξ）‎ E（ξ）==1…‎ ‎　‎ ‎20．在平面直角坐标系xOy中，圆x2+y2=4上的一点P（x0，y0）（x0，y0＞0）处的切线l分别交x轴，y轴于点A，B，以A，B为顶点且以O为中心的椭圆记作C，直线OP交C于M，N两点．‎ ‎（1）若椭圆C的离心率为，求P点的坐标 ‎（2）证明四边形AMBN的面积S＞8．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）运用直线的斜率公式，可得直线l的方程，求得A，B的坐标，可得椭圆的方程，讨论焦点位置，运用离心率公式可得P的坐标；‎ ‎（2）直线OP的斜率为k，依题意有k＞0且k≠1，直线OP的方程为y=kx，直线l的方程为，‎ ‎，求得A，B的坐标，椭圆方程，代入直线y=kx，求得M，N的坐标，可得|OM|，|AB|，运用四边形的面积公式和基本不等式，化简整理，即可得到结论．‎ ‎【解答】解：（1）依题意，，直线l方程为，‎ 令x=0，得，令y=0，得，‎ 即有，‎ 椭圆C的方程为，‎ ‎①若x0＞y0，则椭圆的离心率，‎ 由，得，而，‎ 解得，则；‎ ‎②若x0＜y0，同理可得；‎ 综上可得P点坐标为，；‎ ‎（2）证明：直线OP的斜率为k，依题意有k＞0且k≠1，‎ 直线OP的方程为y=kx，直线l的方程为，‎ 令x=0，得，令y=0，得x=ky0+x0，‎ 可得，‎ 椭圆C的方程，‎ 联立，‎ 解出，‎ 可得，，‎ 即有 ‎=【来源：全,品…中&高*考+网】‎ ‎=‎ ‎=，‎ 即有，‎ ‎|AB|==‎ ‎==，‎ 可得S=|AB|•|MN|=4（k+）•，‎ 令t=k+（t＞2），则f（t）=t2（1+）=（t2﹣2）++4‎ ‎＞2+4=8，‎ 即有f（t）＞8，故．‎ ‎　‎ ‎21．已知函数f（x）=aex+bxlnx图象上x=1处的切线方程为y=2ex﹣e．‎ ‎（Ⅰ）求实数a和b的值；‎ ‎（Ⅱ）求函数g（x）=f（x）﹣ex2的最小值．‎ ‎【考点】利用导数求闭区间上函数的最值；利用导数研究曲线上某点切线方程．‎ ‎【分析】（Ⅰ）求函数的导数，利用导数的几何意义建立方程关系即可求实数a和b的值；‎ ‎（Ⅱ）求函数g（x）=f（x）﹣ex2的导数，研究函数的单调性，判断函数的极值和最值关系即可求g（x）的最小值．‎ ‎【解答】解：（Ⅰ）函数的导数f′（x）=aex+blnx+bx=aex+blnx+b，‎ 则f′（1）=ae+b，‎ ‎∵f（x）=aex+bxlnx图象上x=1处的切线方程为y=2ex﹣e．‎ ‎∴当x=1时，y=2e﹣e=e，即切点坐标为（1，e），‎ 则切线斜率k=f′（1）=ae+b=2e，‎ f（1）=ae+bln1=ae=e，‎ 得a=1，b=e；‎ ‎（Ⅱ）∵a=1，b=e，∴f（x）=ex+exlnx 则函数g（x）=f（x）﹣ex2=ex+exlnx﹣ex2，‎ 函数的定义域为（0，+∞），‎ 则函数的导数g′（x）=ex+elnx+e﹣2e=ex+elnx﹣e 则g′（x）=ex+elnx﹣e在（0，+∞）上为增函数，‎ ‎∵g′（1）=e+eln1+e=e﹣e=0，‎ ‎∴当x＞1时，g′（x）＞0，函数g（x）递增，‎ 当0＜x＜1时，g′（x）＜0，函数g（x）递减，‎ 即当x=1时，g（x）取得极小值，同时也是最小值g（1）=e﹣e=0，‎ 即g（x）=f（x）﹣ex2的最小值是0．‎ ‎　‎ 选考题（二选一）[选修4-1：几何证明选讲]‎ ‎2‎ ‎[选修4-4：坐标系与参数方程]‎ ‎23．在平面直角坐标系xoy中，直线，（t为参数）与抛物线y2=2px（p＞0）相交于横坐标分别为x1，x2的A，B两点 ‎（1）求证：x02=x1x2；‎ ‎（2）若OA⊥OB，求x0的值．‎ ‎【考点】抛物线的简单性质；参数方程化成普通方程．‎ ‎【分析】（1）联立直线与抛物线方程的方程组，利用参数的几何意义化简求解即可．‎ ‎（2）通过向量垂直的充要条件，化简求解即可．‎ ‎【解答】‎ 解：（1）设直线…①与抛物线y2=2px（p＞0）…②‎ 交于点A（x1，y1），B（x2，y2），∴α≠0‎ 把①代入②，得关于t的一元二次方程 t2sin2α﹣2tpcosα﹣2px0=0，‎ 设点A，B所对应的参数分别为t1，t2，则，…③‎ ‎∴…④‎ 把③代入④得…．‎ ‎（2）∵OA⊥OB，∴x1x2+y1y2=0，由（Ⅰ）知，‎ 又y1=t1sinα，y2=t2sinα，∴，‎ 由③知，∴x0=2p． …‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．已知a，b∈R+，设x=，y=，求证：‎ ‎（1）xy≥ab；‎ ‎（2）x+y≤a+b．‎ ‎【考点】基本不等式．‎ ‎【分析】（1）利用基本不等式的性质即可得出．‎ ‎（2）通过平方作差利用乘法公式即可得出．‎ ‎【解答】证明：（1）∵a，b∈R+，x=，y=，‎ ‎∴xy=≥=ab，当且仅当a=b时取等号．‎ ‎（2）∵a，b∈R+，x+y=+，‎ 则（a+b）2﹣（x+y）2=（a+b）2﹣=﹣，‎ 而（a+b）4﹣（a﹣b）4=8ab（a2+b2），∴（a+b）4﹣8ab（a2+b2）=（a﹣b）4，‎ ‎∴（a+b）2≥，‎ ‎∴（a+b）2﹣（x+y）2≥0，‎ ‎∴a+b≥x+y．‎