数学卷·2019届云南省曲靖市沾益县第一中学高二上学期第二次月考(2017-11)
高二年级上学期第二次月考试卷
姓名:__________ 班级:__________考号:__________
一、单选题(共12题;共60分)
1、“点在直线y=x+1上”是“数列为等差数列”的( )
A、充分但不必要条件B、必要但不充分条件
C、充要条件D、既不充分不必要条件
2、在中,已知,则角A等于 ( )
A、B、 C、D、
3、“”是“”的( )
A、充分而不必要条件B、必要而不充分条件
C、充分必要条件D、既不充分也不必要条件
4、命题“如果x≥a2+b2,那么x≥2ab”的逆否命题是( )
A.如果x
2011C、i≤1005D、i>1005
6、已知p,q,r是三个命题,若p是r的充要条件,且q是r的必要条件,则q是p的( )
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
7、已知等差数列的通项公式,则等于( )
A、1B、2C、0D、3
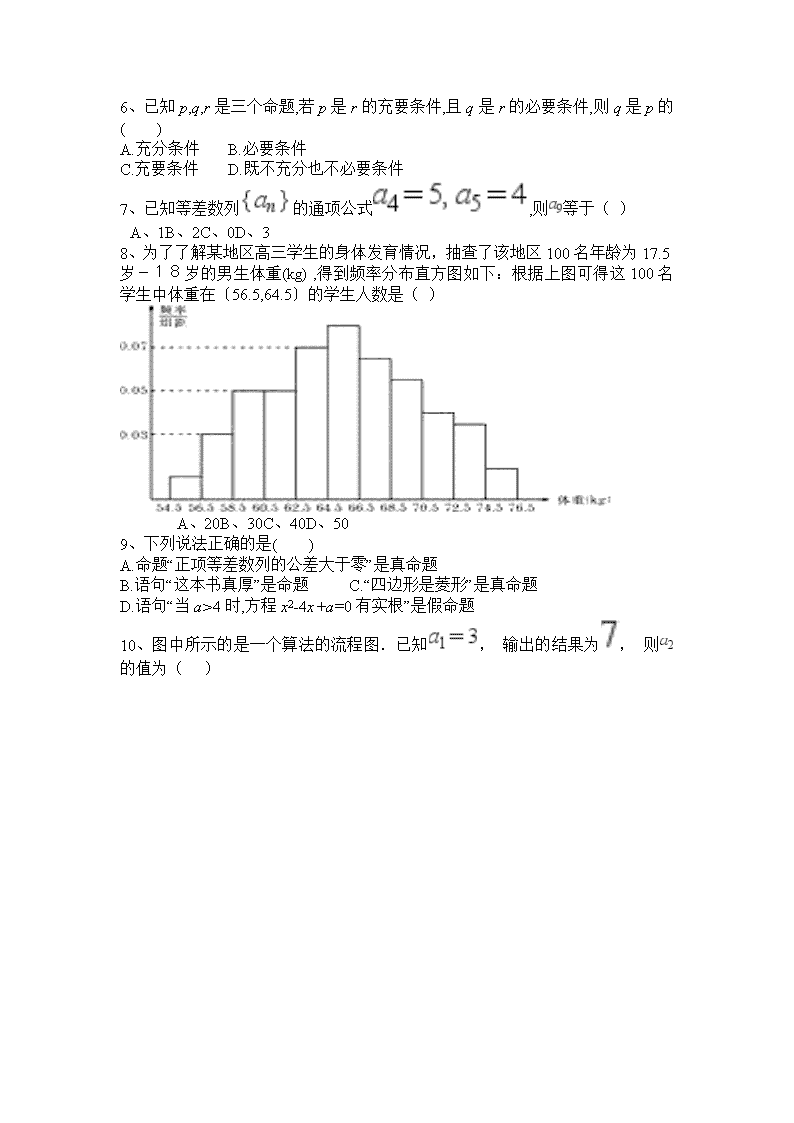
8、为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( )
A、20B、30C、40D、50
9、下列说法正确的是( )
A.命题“正项等差数列的公差大于零”是真命题
B.语句“这本书真厚”是命题 C.“四边形是菱形”是真命题
D.语句“当a>4时,方程x2-4x+a=0有实根”是假命题
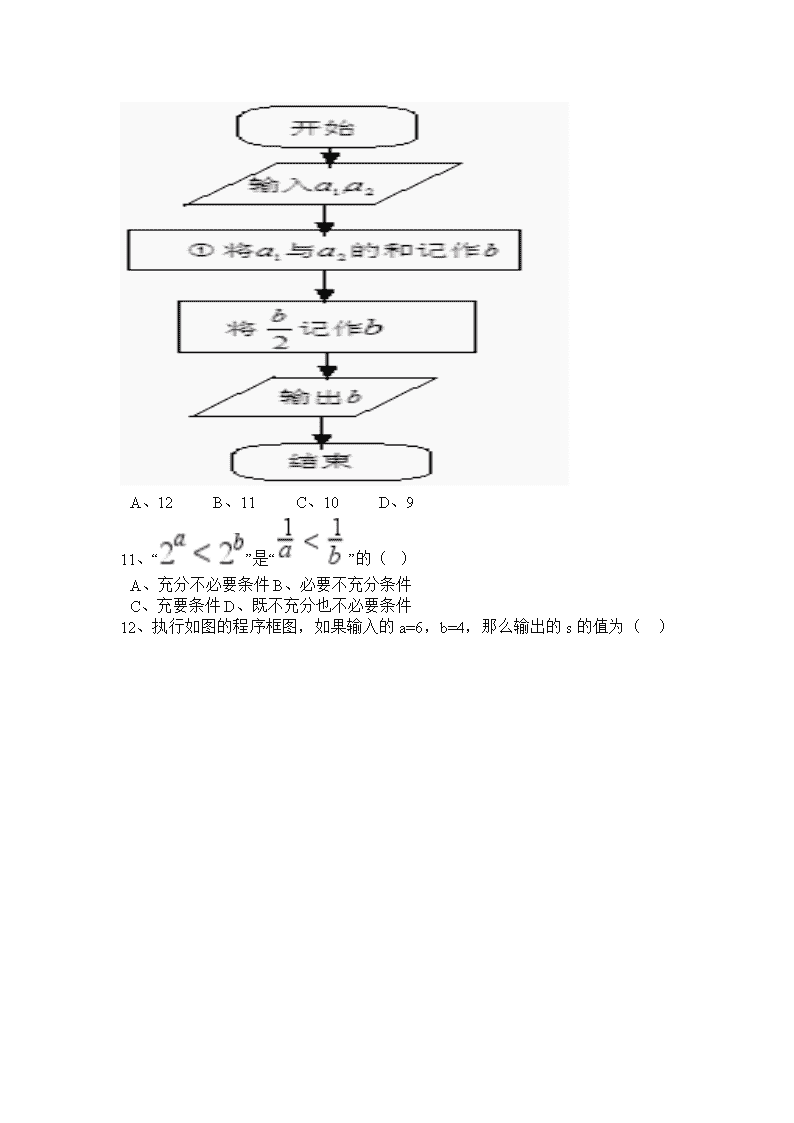
10、图中所示的是一个算法的流程图.已知, 输出的结果为, 则的值为( )
A、12 B、11 C、10 D、9
11、“”是“”的( )
A、充分不必要条件B、必要不充分条件
C、充要条件D、既不充分也不必要条件
12、执行如图的程序框图,如果输入的a=6,b=4,那么输出的s的值为( )
A、17B、22C、18D、20
二、填空题(共5题;共20分)
13、从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是________.
14、若数a1 , a2 , a3 , a4 , a5的标准差为2,则数3a1﹣2,3a2﹣2,3a3﹣2,3a4﹣2,3a5﹣2的方差为________.
15、命题“若a>b,则2a>2b﹣1”的否命题为________.
16、在等差数列{an}中,若a1+a3+a5=3,则a2+a4等于________.
三、解答题(共6题;共70分)
17、如图,已知AB与CD是异面直线,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=G,BC∩α=H.求证:四边形EFGH是平行四边形.
18、中央二台经济生活频道,在主持人马斌主持的“购物街”栏目中,有一个幸运转盘游戏该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲、乙两名入选观众每人都有两次转动盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记;且规定:若某人在第一次转动后,认为分值理想,则可以放弃第二次机会,得分按第一次所指的数记,两人中得分多者为优胜,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85,试回答以下问题:
(Ⅰ)如果甲选择第二次转动,求甲得0分的概率;
(Ⅱ)如果甲放弃了第二次机会,求乙选手获胜的概率.
19、如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?
20、已知直线l经过两点(2,1),(6,3).
(1)求直线l的方程;
(2)圆C的圆心在直线l上,且过点(2,0)和(3,1),求圆C的方程.
21、已知下列三个方程:
x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0,若至少有一个方程有实根,求实数a的取值范围.
22、某厂商调查甲乙两种不同型号汽车在10个不同地区卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图,为了鼓励卖场,在同型号汽车的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”
(1)求在这10个卖场中,甲型号汽车的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号汽车销售量的平均数为26.7,求a<b的概率;
(3)若a=1,记乙型号汽车销售量的方差为s2 , 根据茎叶图推断b为何值时,s2达到最小值(只写出结论) 注:方差 其中 为x1 , x2 , …,xn的平均数.
答案解析部分
一、单选题
1、【答案】A
【考点】等差数列的通项公式,等差数列与一次函数的关系
【解析】【解答】根据题意,由于点在直线, 则可知
, 因此可知为等差数列,但是反之当数列为等差数列时,通项公式就不唯一了,因此不能推出条件,那么将诶和充分条件的判定,可知选A.
【分析】解决该试题的关键是对于点在线上的理解和翻译,从而得到其通项公式,然后结合等差数列的定义来判定是否成立。同时要明白等差数列的通项公式与一次函数的关系,属于基础题。
2、【答案】C
【考点】余弦定理的应用
【解析】【分析】.选C
【点评】要知道余弦定理的结构形式,还要掌握余弦定理可解决两类问题:一是已知两边及夹角,解三角形;二是已知三边,解三角形。.
3、【答案】A
【考点】必要条件、充分条件与充要条件的判断,三角函数的化简求值
【解析】【分析】若, 则, 所以“”是“”的充分而不必要条件。选A。
【点评】熟练掌握充分必要充要条件的判断。此题为基础题型。
4、【答案】C
【考点】命题的真假判断与应用
5、【答案】A
【考点】程序框图
【解析】【分析】因为每循环一次,i就增加2,所以计算的值,当出现后就要输出S,
故判断框中要填条件i≤2011,选A。
【点评】简单题,关键是理解循环体的意义。
6解析:p是r的充要条件,且q是r的必要条件,故有p⇔r⇒q,即p⇒q,所以q是p的必要条件.
答案:B
7、【答案】C
【考点】等差数列的通项公式
【解析】【分析】本题主要考查了等差数列的通项公式的运用。
【解答】由于等差数列的通项公式中,, 而结合通项公式的性质有=+5d=5+5(-1)=0,故选C。
【点评】解决该试题的关键是能够熟练的运用通项公式的性质,联立方程组得到首项和公差,进而得到第n项的值。
8、【答案】C
【考点】频率分布直方图
【解析】【分析】由图可知:则56.5~64.5段的频率为(0.03+0.05×2+0.07)×2=0.4,
则频数为100×0.4=40人.
故选C.
9、答案:D
10、【答案】B
【考点】程序框图
【解析】【解答】由已知,=7,所以=11,故选B。。
【分析】简单题,关键是读懂各个“框”的语句意义。
11、【答案】D
【考点】必要条件、充分条件与充要条件的判断
【解析】【解答】由得,, 若或则, 若, 则, 若, 故既不是充分也不是必要条件,选D.
12、【答案】D
【考点】程序框图
【解析】【解答】解:模拟执行程序,可得 a=6,b=4,n=0,s=6
执行循环体,a=﹣2,b=6,a=4,s=10,n=1
不满足条件s>16,执行循环体,a=2,b=4,a=6,s=16,n=2
不满足条件s>16,执行循环体,a=﹣2,b=6,a=4,s=20,n=3
满足条件s>16,退出循环,可得输出S的值为20.
故选:D.
【分析】模拟执行程序,根据赋值语句的功能依次写出每次循环得到的a,b,s,n的值,当s=20时满足条件s>16,退出循环,输出S的值为20.
二、填空题
13、【答案】
【考点】古典概型及其概率计算公式
【解析】【解答】解:从2,3,8,9中任取两个不同的数字,分别记为a,b,基本事件总数n= =12,
logab为整数满足的基本事件个数为(2,8),(3,9),共2个,
∴logab为整数的概率p= .故答案为: .
【分析】由已知条件先求出基本事件总数,再利用列举法求出logab为整数满足的基本事件个数,由此能求出logab为整数的概率;本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.
14、【答案】36
【考点】极差、方差与标准差
【解析】【解答】解:数a1 , a2 , a3 , a4 , a5的标准差为2,
则数a1 , a2 , a3 , a4 , a5的方差为4,
∴数3a1﹣2,3a2﹣2,3a3﹣2,3a4﹣2,3a5﹣2的方差为4×32=36,
故答案为:36
【分析】根据方差是标准差的平方,数据增加a,方差不变,数据扩大a,方差扩大a2倍,可得答案.
15、【答案】若a≤b,则2a≤2b﹣1
【考点】四种命题,命题的否定
【解析】【解答】解:命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”.
故答案为若a≤b,则2a≤2b﹣1.
【分析】写出一个命题的否命题的关键是正确找出原命题的条件和结论.
16、【答案】2
【考点】等差数列的通项公式
【解析】【解答】解:∵等差数列an中,a1+a5=2a3 , 又由题意a1+a3+a5=3,
∴3a3=3,a3=1,
则a2+a4=2a3=2.
故答案是:2.
【分析】根据等差数列的性质,利用p+q=m+n时,ap+aq=am+an , 求出a3的值,进而可得到a2+a4的值.
一、选择题
1.A
2.C
3.A
4.C
5.A
6.B
7.C
8.C
9.D
10.B
11.D
12.D
二、 填空题
13. 14.36 15. 若a≤b,则2a≤2b﹣1 16. 2
三、解答题
17【答案】证明:因为AB∥平面α,AB⊂平面ABC,
平面ABC∩平面α=EH,所以AB∥EH.
因为AB∥平面α,AB⊂平面ABD,
平面ABD∩平面α=FG,所以AB∥FG,所以EH∥FG,
同理由CD∥平面α可证EF∥GH,
所以四边形EFGH是平行四边形.
出的首项和公差直接代入等差数列的前n项和公式求解;(Ⅲ)利用二次函数的性质求前n项和的最大值.
18、【答案】解:(Ⅰ)若甲第二次转动盘指针所指的数字是5,10,15这三种情况,则甲的得分不是0,否则,甲得0分.
故甲得0分的概率为 1﹣ = .
(Ⅱ)用ξ1、ξ2分别表示乙第一次、第二次转动时,指针所指分数,
当乙1次转动盘就赢取甲的概率P′= ,(此时,指针指的数为 90,95,100,共三种情况).
下面计算当乙2次转动盘赢取甲的概率.
若乙第一次转动盘 指针所指分数 ξ1=5,则乙赢取甲时,乙第二次转动时,指针所指分数为85、90、或95,
故此时乙赢取甲的概率的概率 P1= .
若乙第一次转动盘 指针所指分数 ξ1=10,则乙赢取甲时,乙第二次转动时,指针所指分数为80、85、或90,
故此时乙赢取甲的概率的概率 P2= ,
…,
以此类推,若乙第一次转动盘 指针所指分数 ξ1=85,则乙赢取甲时,乙第二次转动时,指针所指分数为5、10、或15,
故此时乙赢取甲的概率的概率 P17= ,
故当乙2次转动盘赢取甲的概率为 P=P1+P2+P3+…+P17= = .
综上可得,乙赢取甲的概率的概率为 P+P′= + =
【考点】互斥事件的概率加法公式,几何概型
【解析】【分析】(Ⅰ)若甲第二次转动盘指针所指的数字是5,10,15这三种情况,则甲的得分不是0,否则,甲得0分. 用1减去得甲得不是0分的概率,记得所求.(Ⅱ)当乙1次转动盘就赢取甲的概率P′的值,再求出当乙转动盘2次,赢得甲的概率P=P1+P2+…+P17 的值,再把这两个概率相加,记得所求.
19、【答案】解:设汽车前进20千米后到达点B, 则在△ABC中,AC=31,BC=20,AB=21,
由余弦定理得cosC= = = ,
则sinC= = ,
由已知∠AMC=60°,∴∠MAC=120°﹣C,
sin∠MAC=sin(120°﹣C)=sin120°cosC﹣cos120°sinC=
在△MAC中,由正弦定理得 = =35
从而有MB=MC﹣BC=15(千米)
所以汽车还需行驶15千米,才能到达M汽车站.
【考点】正弦定理的应用,解三角形的实际应用
【解析】【分析】在△ABC中,由余弦定理得cosC,然后利用同角三角函数的基本关系式求出sinC,通过sin∠MAC=sin(120°﹣C),在△MAC中求出MC,然后求解MB即可.
二、综合题
20、【答案】(1)解:∵直线l经过两点(2,1),(6,3), ∴直线l的方程为y﹣1= (x﹣2),即x﹣2y=0
(2)解:圆C的圆心在直线l上,设圆心为(2a,a), ∵过点(2,0)和(3,1),
∴(2a﹣2)2+a2=(2a﹣3)2+(a﹣1)2 ,
∴a=1,
∴圆C的方程(x﹣2)2+(y﹣1)2=1
【考点】直线与圆相交的性质
【解析】【分析】(1)求出直线的斜率,可得直线l的方程;(2)设圆心为(2a,a),利用两点间的距离公式建立方程,求出a,即可求圆C的方程.
21、分析三个方程的根有如下四种情况:
(1)三个方程都无实根;
.
若按分类讨论,则需分三种情况,且(2)(3)又分多种情况,显然运算量太大,若注意到(2)(3)(4)可合并为至少有一个方程有实根,利用“补集”的思想,问题即可等价转化.
解:假设三个方程都无实根,
则
故若三个方程中至少有一个方程有实根,
则a的取值范围是a≥-1或a≤
22、【答案】(1)解:根据茎叶图得到甲组数据的平均值: = (10+10+18+14+22+25+27+30+41+43)=24.
∵该厂商将销售量高于数据平均数的卖场命名为该型号的“星级卖场”,
∴在这10个卖场中,甲型号汽车的“星级卖场”的个数为5个.
(2)解:记事件A为“a<b”, 乙组数据的平均值:
= (10+18+20+22+23+31+32+a+a+30+30+43)=26.7,
∴a+b=8,
和取值共9种,分别为:
(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1),(8,0),
其中a<b的有4种,
∴a<b的概率P(A)= .
(3)解:b=0时,S2达到最小值.
【考点】极差、方差与标准差,古典概型及其概率计算公式
【解析】【分析】(1)根据茎叶图得到甲组数据的平均值,由此能求出在这10个卖场中,甲型号汽车的“星级卖场”的个数.(2)记事件A为“a<b”,求出乙组数据的平均值,由此利用列举法能求出a<b的概率.(3)由方差的性质能求出b=0时,S2达到最小值.