数学文卷·2017届江西省上高二中高三下学期开学考试(第七次)(2017
2017届高三年级第七次月考数学(文科)试卷
一、选择题(共12小题,每小题5分)
1.已知集合A={x|log2x<1},B={x|0
0}.若A∪B=B,则c的取值范围是( )
A.(0,1] B.[1,+∞) C.(0,2] D.[2,+∞)
2.复数满足,则等于( )
A. B. C. D.
3.在数列中,,则( )
A. B. C. D.
4.在面积为S的矩形ABCD内随机取一点P,则△PBC的面积小于的概率是( )
A. B. C. D.
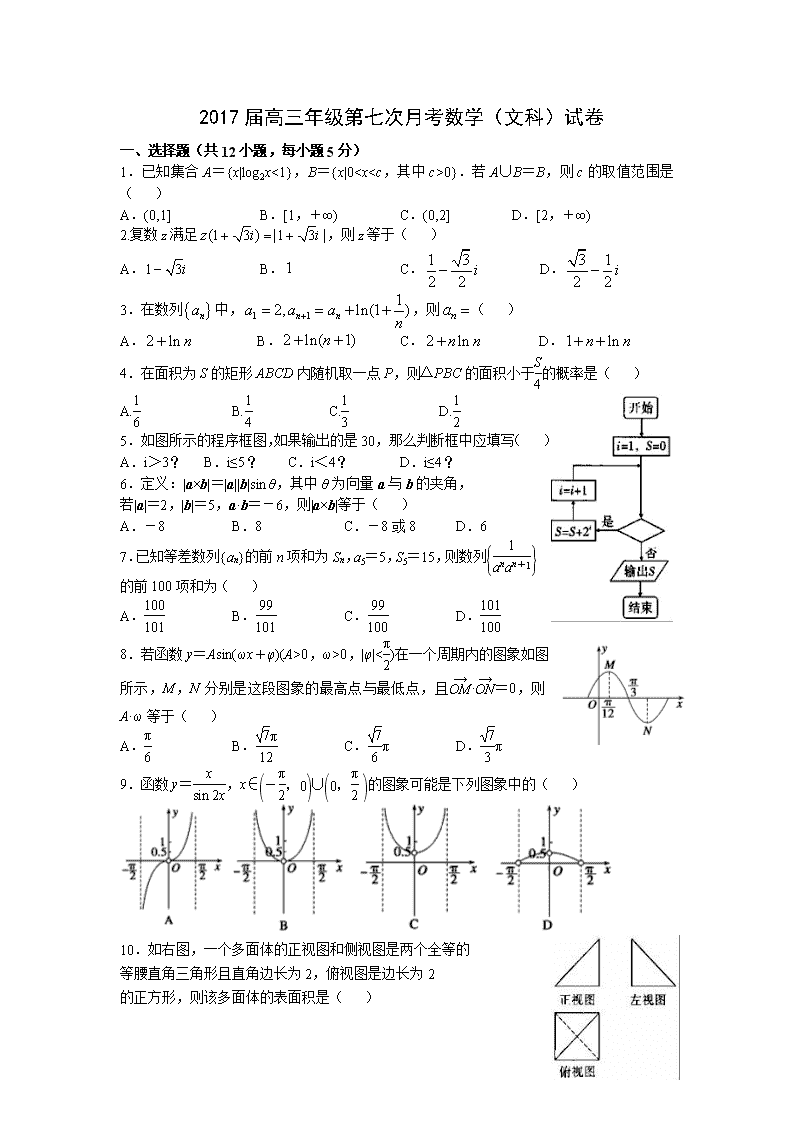
5.如图所示的程序框图,如果输出的是30,那么判断框中应填写( )
A.i>3? B.i≤5? C.i<4? D.i≤4?
6.定义:|a×b|=|a||b|sin θ,其中θ为向量a与b的夹角,
若|a|=2,|b|=5,a·b=-6,则|a×b|等于( )
A.-8 B.8 C.-8或8 D.6
7.已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列的前100项和为( )
A. B. C. D.
8.若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象如图所示,M,N分别是这段图象的最高点与最低点,且·=0,则A·ω等于( )
A. B. C.π D.π
9.函数y=,x∈∪的图象可能是下列图象中的( )
10.如右图,一个多面体的正视图和侧视图是两个全等的
等腰直角三角形且直角边长为2,俯视图是边长为2
的正方形,则该多面体的表面积是( )
A. B.
C. D.
11.已知是单位圆上互不相同的三点,且满足,则的最小值为( )
A. B. C. D.
12.在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”.在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个正方形;
②到原点的“折线距离”等于1的点的集合是一个圆;
③到M(-1,0),N(1,0)两点的“折线距离”相等的点的轨迹方程是x=0;
④到M(-1,0),N(1,0)两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
其中真命题有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共4小题,每小题5分)
13.设直线x-my-1=0与圆(x-1)2+(y-2)2=4相交于A,B两点,且弦AB的长为2,则实数m的值是________.
14.若不等式组表示的区域为一个锐角三角形及其内部,则实数的范围是 .
15.所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥中,是的中点,且,底面边长,则其外接球的表面积为 .
16.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=()x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是________.
三、解答题(共70分)
17.(本小题满分10分) 在中,分别是角的对边,
.
(1)若且角为锐角,求角的大小;
(2)在(1)的条件下,若,求的值
18.(本小题满分12分)已知数列的前项和为,且是等差数列.
(1)求数列的通项公式;
(2)若,设,求数列的前项和为.
19.(本题满分为12分) 已知函数.
(1)求函数的单调增区间;
(2)在中,分别是角的对边,且,求的面积.
20.(本小题满分12分)元旦前夕,某校高三某班举行庆祝晚会,人人准备了才艺,由于时间限制不能全部展示,于是找四张红色纸片和四张绿色纸片上分别写1,2,3,4,确定由谁展示才艺的规则如下:
①每个人先分别抽取红色纸片和绿色纸片各一次,并将上面的数字相加的和记为;
②当或时,即有资格展现才艺;当时,即被迫放弃展示.
(1)请你写出红绿纸片所有可能的组合(例如);
(2)求甲同学能取得展示才艺资格的概率.
21.(本小题满分12分)如图,在底面是菱形的四棱柱中,,
,,点在上.
(1)求证:平面;
(2)当为何值时,平面,并求出此时
直线与平面之间的距离.
22.(本小题满分12分)已知函数,.
(1)当时,求函数在处的切线方程;
(2)令,求函数的极值;
(3)若,正实数满足,证明:
2017届高三年级第七次月考数学(文科)试卷答题卡
一、选择题(共12小题,每小题5分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(共4小题,每小题5分)
13、 14、 15、 16、
三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17、(本题满分10分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分12分)
2017届高三年级第七次月考数学(文科)试卷参考答案
【答案】DCADD BACCA BC
13.± 14. 15. 16.(,2)
17.解析:(1) ,,解得
又角为锐角, 5分
(2) 在中,则,
,由正弦定理得,解得 10分
18.【解析】(1)由是等差数列知…①,
当时,,则;………… 2分
当时,…②,①-②得,即;………… 4分
故数列是首项为1,公比为2的等比数列,所以. ………… 6分
(2),,………… 8分
…③
…④
③-④得
. ………… 12分
19. 解:(1)∵=
==. 3分
∴函数的单调递增区间是. 5分
(2)∵,∴.
又,∴.
∴. 7分
在中,∵,
∴,即.
∴. 10分
∴ 12分
20.解:(1)取得这些可能的值的红绿卡片可能的组合为:
(2)从(1)中可知红绿卡片所有可能组合对共有16个.
满足当或的红绿卡片组合对有:,,共9对.
所以甲同学取得展示才艺资格的概率为.
21.(1)证明:因为底面为菱形,,所以,
在中,由知,
同理,
又因为,所以平面.
(2)解:当时,平面.证明如下:
连结交于,当时,即点为的中点时,连结,则,
所以平面,
所以直线与平面之间的距离等于点到平面的距离.
因为点为的中点,可转化为到平面的距离,,
设的中点为,连结,则,
所以平面,且,可求得,
所以,
又,,,,
所以(表示点到平面的距离),,
所以直线与平面之间的距离为.
22、解:(1)当时,,则,所以切点为,
又,则切线斜率,
故切线方程为,即.………………………………………3分
(2),
则,……………………………………4分
当时,∵,∴.
∴在上是递增函数,函数无极值点,………………………………5分
当时,,
令得.
∴当时,;当时,.
因此在上是增函数,在上是减函数. ……………………………7分
∴时,有极大值.
综上,当时,函数无极值;
当时,函数有极大值.……………………………………8分
(3)证明:当时,,.
由,即,
从而
令,则由得:,
可知,在区间上单调递减,在区间上单调递增.
∴,∴,
∵,,∴成立. …………………………12分