福建省漳州市2020届高三高考适应性测试数学（理）

福建省漳州市2020届高三高考适应性测试数学（理）

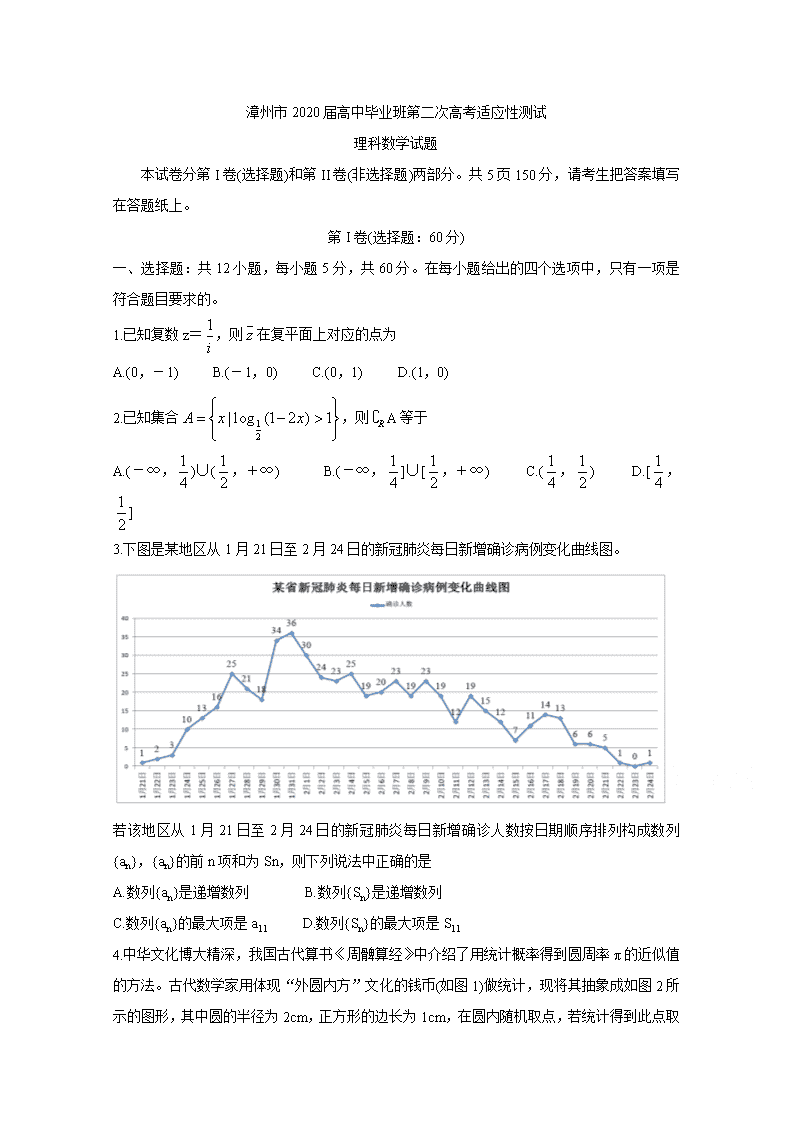
漳州市2020届高中毕业班第二次高考适应性测试 理科数学试题 本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共5页150分，请考生把答案填写在答题纸上。‎ 第I卷(选择题：60分)‎ 一、选择题：共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知复数z＝，则在复平面上对应的点为 A.(0，－1) B.(－1，0) C.(0，1) D.(1，0)‎ ‎2.已知集合，则A等于 A.(－∞，)∪(，＋∞) B.(－∞，]∪[，＋∞) C.(，) D.[，]‎ ‎3.下图是某地区从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图。‎ 若该地区从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列{an}，{an}的前n项和为Sn，则下列说法中正确的是 A.数列{an}是递增数列 B.数列{Sn}是递增数列 C.数列{an}的最大项是a11 D.数列{Sn}的最大项是S11‎ ‎4.中华文化博大精深，我国古代算书《周髀算经》中介绍了用统计概率得到圆周率π的近似值的方法。古代数学家用体现“外圆内方”文化的钱币(如图1)做统计，现将其抽象成如图2所示的图形，其中圆的半径为2cm，正方形的边长为1cm，在圆内随机取点，‎ 若统计得到此点取自阴影部分的概率是p，则圆周率π的近似值为 A. B. C. D.‎ ‎5.已知点(1，2)在双曲线的渐近线上，则该双曲线的离心率为 A. B. C. D.‎ ‎6.在△ABC中，AB＝2，∠ABC＝30°，AD是BC边上的高，则等于 A.0 B. C.2 D.1‎ ‎7.已知函数，则下列说法错误的是 A.g(x)的定义域是R B.g(x)是偶函数 C.g(x)在(0，＋∞)单调递减 D.g(x)的最小值为1‎ ‎8.已知△ABC的内角A，B，C的对边分别为a，b，c，A＝60°，b＝3c，角A的平分线交BC于点D，且BD＝，则cos∠ADB的值为 A. B. C. D.±‎ ‎9.若正四棱柱ABCD－A1B1C1D1的底面边长为2，外接球的表面积为40π，四边形ABCD和BCC1B1的外接圆的圆心分别为M，N，则直线MN与CD1所成的角的余弦值是 A. B. C. D. ‎ ‎10.已知函数f(x)＝－x3＋x2＋ln|x|－a有三个零点，则实数a的取值范围是 A.a<0 B.a≤1 C.a>0 D.a>1‎ ‎11.如图，已知△ABC的三个顶点均在抛物线x2＝4y上，AB经过抛物线的焦点F，点D为AC中点。若点D的纵坐标等于线段AC的长度减去1，则当∠AFC最大时，线段AB的长度为 A.12 B.14 C.10 D.16‎ ‎12.已知函数f(x)＝sin(ωx＋φ)(ω>0，φ∈[0，])的图象经过点(0，)，若关于x的方程f(x)＝－1在[，π]上恰有一个实数解，则ω的取值范围是 A.[，) B.[，8] C.[，20] D.[，20]‎ 第II卷(非选择题：90分)‎ 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎13.若sinα＝，则cos2α＝ 。‎ ‎14.若(1＋mx)6＝a0＋a1x＋a2x2＋…＋a6x6，且a1＋a2＋…＋a6＝63，则实数m＝ 。‎ ‎15.定义在R上的函数f(x)为奇函数，f(1)＝1，又g(x)＝f(x＋2)也是奇函数，则f(2020)＝ 。‎ ‎16.已知正方体ABCD－A1B1C1D1的棱长为4，点P是AA1的中点，点M在侧面AA1B1B内，若D1M⊥CP，则△BCM面积的最小值为 。‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22题、第23题为选考题，考生根据要求作答。‎ ‎(一)必考题：共60分。‎ ‎17.(12分)‎ 已知数列{an}的前n项和为Sn，an>0，2Sn＝an2＋an，n∈N*。‎ ‎(1)求an；‎ ‎(2)若bn＝，数列{bn}的前n项和为Tn，求Tn。‎ ‎18.(12分)‎ 在如图所示的六面体中，四边形ABCD是边长为2的正方形，四边形ABEF是梯形，AF//BE，平面ABCD⊥平面ABEF，BE＝2AF＝2，EF＝。‎ ‎ ‎ ‎(1)在图中作出平面ABCD与平面DEF的交线，并写出作图步骤，但不要求证明；‎ ‎(2)求证：AC//平面DEF；‎ ‎(3)求平面ABEF与平面ECD所成锐二面角的余弦值。‎ ‎19.(12分)‎ 眼保健操是一种眼睛的保健体操，主要是通过按摩眼部穴位，调整眼及头部的血液循环，调节肌肉，改善眼的疲劳，达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果，在应届高三的全体800名学生中随机抽取了100名学生进行视力检查，并得到如图的频率分布直方图。‎ ‎(1)若直方图中后三组的频数成等差数列，试估计全年级视力在5.0以上的人数；‎ ‎(2)为了研究学生的视力与眼保健操是否有关系，对年级不做眼保健操和坚持做眼保健操的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?‎ ‎(3)在(2)中调查的100名学生中，按照分层抽样在不近视的学生中抽取8人，进一步调查他们良好的护眼习惯，在这8人中任取2人，记坚持做眼保健操的学生人数为X，求X的分布列和数学期望。‎ 附：‎ ‎20.(12分)‎ 已知椭圆与双曲线有相同的焦点坐标，且点(，)在椭圆上。‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设A、B分别是椭圆的左、右顶点，动点M满足MB⊥AB，垂足为B，连接AM交椭圆于点P(异于A)，则是否存在定点T，使得以线段MP为直径的圆恒过直线BP与MT的交点Q，若存在，求出点T的坐标；若不存在，请说明理由。‎ ‎21.(12分)‎ 已知函数f(x)＝lnx＋(a－)x2－2ax，a∈R。‎ ‎(1)讨论f(x)的单调性；‎ ‎(2)若f(x)在定义域内是增函数，且存在不相等的正实数x1，x2，使得f(x1)＋f(x2)＝－3，证明：x1＋x2>2。‎ ‎(二)选考题：共10分。请考生在第22、23两题中任选一题作答。如果多做，则按所做第一个题目计分。‎ ‎22.[选修4－4：坐标系与参数方程](10分)‎ 已知曲线C的参数方程为(α为参数)，P是曲线C上的点且对应的参数为β，0<β<。直线l过点P且倾斜角为π－β。‎ ‎(1)求曲线C的普通方程和直线l的参数方程；‎ ‎(2)已知直线l与x轴，y轴分别交于A，B，求证：|PA|·|PB|为定值。‎ ‎23.[选修4－5：不等式选讲](10分)‎ 已知a>0，b>0，a2＋4b2＝＋3。‎ ‎(1)求证：ab≤1；‎ ‎(2)若b>a，求证：。‎