2020届二轮复习三角函数（一）学案（全国通用）

2020届二轮复习三角函数（一）学案（全国通用）

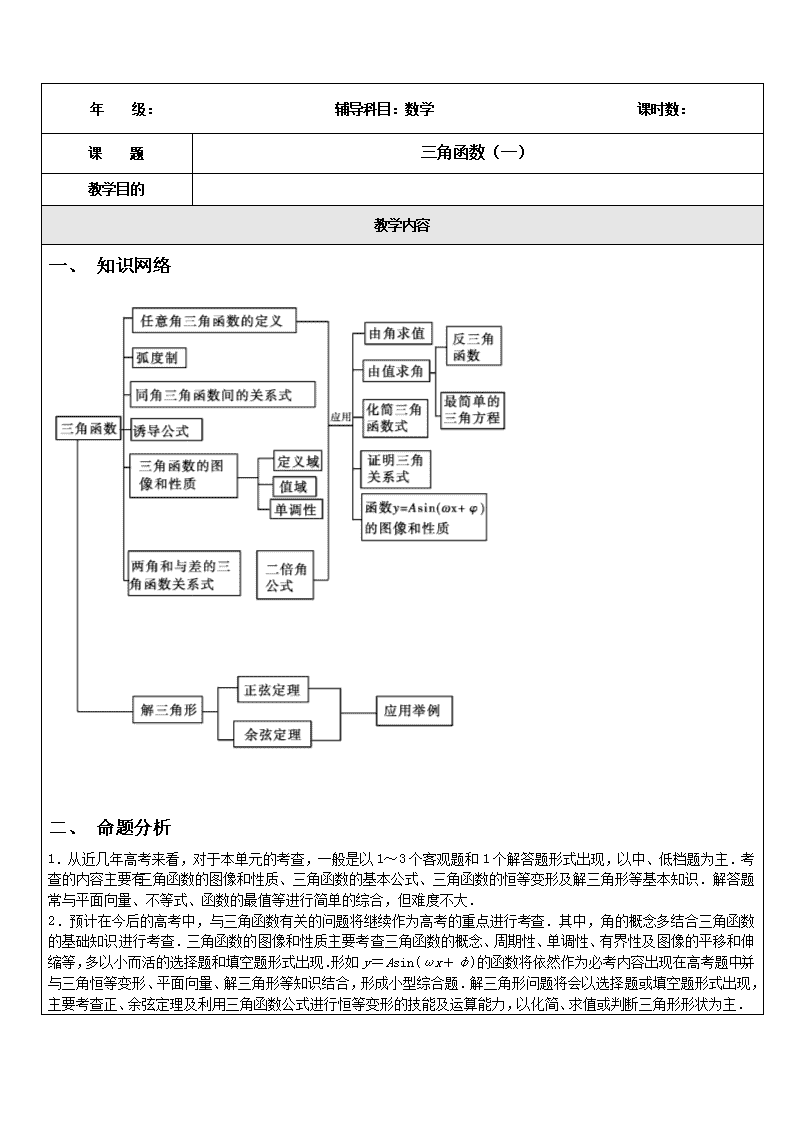
年 级： 辅导科目：数学 课时数： 课 题 三角函数（一） 教学目的 教学内容 一、 知识网络 二、 命题分析 1．从近几年高考来看，对于本单元的考查，一般是以 1～3 个客观题和 1 个解答题形式出现，以中、低档题为主．考 查的内容主要有：三角函数的图像和性质、三角函数的基本公式、三角函数的恒等变形及解三角形等基本知识．解答 题常与平面向量、不等式、函数的最值等进行简单的综合，但难度不大． 2．预计在今后的高考中，与三角函数有关的问题将继续作为高考的重点进行考查．其中，角的概念多结合三角函数 的基础知识进行考查．三角函数的图像和性质主要考查三角函数的概念、周期性、单调性、有界性及图像的平移和伸 缩等，多以小而活的选择题和填空题形式出现．形如 y＝Asin(ωx＋φ)的函数将依然作为必考内容出现在高考题中，并 与三角恒等变形、平面向量、解三角形等知识结合，形成小型综合题．解三角形问题将会以选择题或填空题形式出现， 主要考查正、余弦定理及利用三角函数公式进行恒等变形的技能及运算能力，以化简、求值或判断三角形形状为主． 三、复习建议 1．复习中要注意几个知识点的综合应用，这就要求我们要从整体上掌握本单元的知识结构，注重知识点之间的联系 和综合运用并加大练习力度，解决公式的综合运用问题，提高计算能力． 2．掌握正弦函数、余弦函数和 y＝Asin(ωx＋φ)的图像和性质，这是历年高考的重点． 3．在训练中，强化“变换”意识，但训练难度不宜过大，立足课本，掌握常见问题的解法，熟记课本中出现的公式 和常用到的重要的结论，并注意其变形应用． 4．从“整体处理”的思想高度去认识理解运用“五点法”，尤其是对y＝Asin(ωx＋φ)的图像和性质的理解、应用． 5．在复习过程中，要着重加强三角函数应用意识的训练． 四、知识讲解 第一节 任意角、弧度制及三角函数定义 （一）高考目标 考纲解读 1．了解任意角的概念． 2．了解弧度制的概念，能进行弧度与角度的互化． 3．理解任意角三角函数(正弦、余弦、正切)的定义． 考向预测 1．三角函数的定义及应用是本节考查重点，注意三角函数值符号的确定． 2．主要以选择题、填空题的形式考查． （二）课前自主预习 知识梳理 1．角的有关概念 (1)角：角可以看成由 绕着端点从一个位置 到另一个位置所成的 .旋转开始时的射线叫做角α的 ，旋转终止时的射线叫做角α的 ，射线的端点叫做角α的 ． (2)角的分类：角分 (按角的旋转方向)． (3)在直角坐标系内讨论角 ①象限角：角的顶点在原点，始边在 上，角的终边在第几象限，就说这个角是 ． ②象限界角：若角的终边在 ，就说这个角不属于任何象限，它叫 ③与角α终边相同的角的集合：{β|β＝k·360°＋α，k∈Z}． (4)弧度制 ①1 弧度的角： 叫做 1 弧度的角． ②规定：正角的弧度数为 ，负角的弧度数为 ，零角的弧度数为 ，|α|＝ l r，l 是以角 α 作为圆心角时 所对圆弧的长，r 为半径． ③以“弧度”作为单位来度量角的单位制叫做弧度制．比值与所取的 r 的大小 ，仅与 有关． ④弧度与角度的换算：360°＝2π弧度；180°＝ 弧度． ⑤弧长公式： ，扇形面积公式：S 扇形＝ 1 2l·r＝ 1 2|α|r2. 2．任意角的三角函数定义 设 α 是一个任意角，角 α 的终边上任意一点 P(x，y)，它与原点的距离为 r(r>0)，那么角 α 的正弦、余弦、 正切分别是：sinα＝ y r，cosα＝ x r，tanα＝ y x，它们都是以角为 ，以比值为 的函数． 3．设角α的顶点在坐标原点，始边与 x 轴正半轴重合，终边与单位圆相交于点 P，过 P 作 PM 垂直于 x 轴于 M，则点 M 是点 P 在 x 轴上的正射影．由三角函数的定义知，点 P 的坐标为 ，即 ，其中 cosα＝ ， sinα＝ ，单位圆与 x 轴的正半轴交于点 A，单位圆在 A 点的切线与α的终边或其反向延长线相交于点 T(T′)，则 tan α＝ .我们把有向线段 OM、MP、AT(或 AT′)叫做α的 ． （三）基础自测 1．与 610°角终边相同的角可表示为(　　) A．k·360°＋230°，k∈Z　 B．k·360°＋250°，k∈Z C．k·360°＋70°，k∈Z D．k·360°＋270°，k∈Z [答案]　B [解析]　由于 610°＝360°＋250°，所以 610°与 250°角的终边相同． 2．已知角 α 的终边经过点( 3，－1)，则角 α 的最小正值是(　　) A. 2π 3 B. 11π 6 C. 5π 6 D. 3π 4 [答案]　B [解析]　∵sinα＝ －1 2 ＝－ 1 2，且 α 的终边在第四象限， ∴α＝ 11 6 π. 3．若－π>θ>－ 3π 2 ，则点(tanθ，sinθ)在(　　) A．第一象限 B．第二象限 C．第三象限 D．第四象限 [答案]　B [解析]　易知θ在第二象限，则 tanθ<0，sinθ>0. 4．若α的终边过点 P(2sin30°，－2cos30°)，则 sinα的值为(　　) A. 1 2 B．－ 1 2 C．－ 3 2 D．－ 3 3 [答案]　C [解析]　P(2sin30°，－2cos30°)即 P(1，－ 3)，∴r＝2，故 sinα＝－ 3 2 ，故选 C. 5．已知角 α 的终边在直线 y＝－3x 上，则 10sinα＋ 3 cosα＝________. [答案]　0 [解析]　设α终边上任一点 P(k，－3k)， 则 r＝ x2＋y2＝ k2＋－3k2＝ 10|k|. 当 k>0 时，r＝ 10k， ∴sinα＝ －3k 10k＝－ 3 10，cosα＝ k 10k＝ 1 10， ∴10sinα＋ 3 cosα＝－3 10＋3 10＝0. 当 k<0 时，r＝－ 10k，∴sinα＝ 3 10，cosα＝－ 1 10，∴10sinα＋ 3 cosα＝0. 6．若 π 4 <θ< π 2 ，则 sinθ、cosθ、tanθ 的大小关系为__________． [答案]　cosθ0)，且 sinθ＝ 2 4 m，求 tanθ，cosθ 的值． [解析]　∵m>0，则 P(－ 3，m)在第二象限， x＝－ 3，y＝m，r＝ 3＋m2， ∴sinθ＝ m 3＋m2， 又∵sinθ＝ 2 4 m＝ m 8，∴ m 3＋m2＝ m 8. 可知 m＝ 5，tanθ＝ m － 3＝－ 15 3 ，cosθ＝ － 3 8 ＝－ 6 4 . （四）典型例题 1.命题方向：判断角所在象限 [例 1]　(1)若 sinθ·cosθ>0，试确定θ所在象限． (2)已知 α 为第二象限角，则 α 2 为第几象限角？ [分析]　(1)先确定 sinθ 与 cosθ 的符号，再判断 θ 所在象限；(2)用不等式表示出α 的范围，讨论可得 α 2 所 在象限． [解析]　(1)由 sinθ·cosθ>0，得Error!① 或Error!② 由①知 θ 在第一象限，由②知 θ 在第三象限， ∴θ 在第一或第三象限． (2)∵α 为第二象限角， ∴2kπ＋ π 2 <α<π＋2kπ，k∈Z. ∴kπ＋ π 4 < α 2 < π 2 ＋kπ，k∈Z. k 为偶数时 k＝2n(n∈Z)，2nπ＋ π 4 < α 2 <2kπ＋ π 2 为第一象限角； k 为奇数时 k＝2n＋1(n∈Z)，2nπ＋ 5π 4 < α 2 <2nπ＋ 3π 2 为第三象限角． ∴ α 2 为第一或第三象限角． [点评]　问题(1)主要是利用三角函数值在各象限的符号来判断，注意θ是满足两个条件的公共解． 问题(2) 主要是利用不等式表示出 α n 的范围，对 k 进行讨论，然后利用终边相同角的特点，即可确定 α n 所在象 限． 跟踪练习 1： 设 θ 为第三象限角，试判断 sin θ 2 cos θ 2 的符号 [解析]　∵θ 为第三象限角，∴2kπ＋π<θ<2kπ＋ 3π 2 (k∈Z)， kπ＋ π 2 < θ 2 0，∴ sin θ 2 cos θ 2 <0.综上可知： sin θ 2 cos θ 2 <0. 2.命题方向：弧长公式及扇形面积公式的应用 [例 2]　已知一扇形的中心角是α，所在圆的半径是 R. (1)若α＝60°，R＝10 cm，求扇形的弧长及该弧所在弓形的面积； (2)若扇形的周长是一定值 C(C>0)，当α为多少弧度时，该扇形有最大面积？ [分析]　(1)直接套用公式 l＝αR 可求弧长，利用 S 弓＝S 扇－S△可求弓形面积． (2)将 S 扇表示为α的函数，转化为函数求最大值问题． [解析]　(1)设弧长为 l，弓形面积为 S 弓， ∵α＝60°＝ π 3 ，R＝10，l＝ 10π 3 ， S 弓＝S 扇－S△＝ 1 2× 10π 3 ×10－ 1 2×102sin60°＝50( π 3 － 3 2 )． (2)解法 1：扇形周长 C＝2R＋l＝2R＋αR. ∴R＝ C 2＋α，∴S 扇＝ 1 2α·R2＝ 1 2α· C2 (2＋α)2＝ C2 2 ×α· 1 α2＋4α＋4＝ C2 2 · 1 α＋ 4 α＋4 ≤ C2 16， ∴当 α＝ 4 α即 α＝2(α＝－2 舍去)时， 扇形面积有最大值 C2 16. 解法 2：由已知 2R＋l＝C，∴R＝ C－l 2 (l0，r＝5a，α 角在第二象限，sinα＝ y r＝ 3a 5a＝ 3 5， cosα＝ x r＝ －4a 5a ＝－ 4 5，tanα＝ y x＝ 3a －4a＝－ 3 4； 若 a<0，r＝－5a，a 角在第四象限， sinα＝－ 3 5，cosα＝ 4 5，tanα＝－ 3 4. 跟踪练习 3： 已知角 α 的终边上一点的坐标为(sin π 3 ，cos π 3 )，则角 α 在[0,2π)内的值为(　　) A. 5π 6 或 π 6 　 B. 2π 3 或 5 3π　 C. π 3 　　　 D. π 6 [答案]　D [解析]　∴sin π 3 >0，cos π 3 <0， ∴点(sin π 3 ，cos π 3 )落在第一象限， 又∵tanα＝ cos π 3 sin π 3 ＝ 3 3 ，∴α＝ π 6 ，故选 D. 4.命题方向：单位圆的应用 已知：α∈(0， π 2 )，求证：sinα<αcosx 成立的 x 的取值范围是______． [答案]　(π 4 ， 5π 4 ) [解析]　由三角函数定义结合三角函数线知，在(0,2π)内，使 sinx>cosx 成立的 x 的取值范围为(π 4 ， 5π 4 ). （五）思想方法点拨： 1．弧度制与角度制不能混用，如 α＝2kπ＋30°(k∈Z)，β＝k·360°＋ π 2 (k∈Z)都是不正确的． PB 2．在学习中要正确区分象限角和象限界角(角的终边落在坐标轴上的角)及它们的表示方法，特别是第一象限的角 {α|k·360°<α0，sinα<0，即该点位于第四象限． 2．如果点 P(sinθcosθ，2cosθ)位于第三象限，那么角 θ 所在的象限是(　　) A．第一象限 B．第二象限 C．第三象限 D．第四象限 [答案]　B [解析]　因为点 P(sinθcosθ，2cosθ)位于第三象限，所以 sinθcosθ<0,2cosθ<0，即Error!，θ 为第二象限角． 3．若角 α 的终边落在直线 y＝－x 上，则 sinα 1－sin2α ＋ 1－cos2α cosα 的值等于(　　) A．0　　　 B．2　　　　 C．－2　　　　 D．2tanα [答案]　A [解析]　∵角 α 的终边在直线 y＝－x 上， ∴α＝kπ＋3π 4 　(k∈Z)，∴sinα 与 cosα 符号相反， ∴ sinα 1－sin2α ＋ 1－cos2α cosα ＝ sinα |cosα|＋|sinα| cosα＝0. 4．已知扇形的周长为 6cm，面积是 2cm2，则扇形的圆心角的弧度数是(　　) A．1 B．4 C．1 或 4 D．2 或 4 [答案]　C [解析]　设扇形圆心角为 αrad，半径为 r，弧长为 l. 则Error!∴Error!或Error! ∴α＝l r＝4 或 α＝1.∴选 C. 5．已知锐角 α 终边上一点 P 的坐标是(2sin2，－2cos2)，则 α 等于(　　) A．2 B．－2 C．2－π 2 D.π 2－2 [答案]　C [解析]　点 P 位于第一象限，且 tanα＝－cot2＝－tan( π 2－2 )＝tan(2－π 2 )， ∵2－π 2∈(0，π 2 )，∴α＝2－π 2. 6．若 A、B、C 为△ABC 的三个内角，且 A0. ∴sinx－cosx<0，从而可得 sinx－cosx＝－ 7 5. (2)由(1)得， 3sin2 x 2－2sin x 2cos x 2＋cos2 x 2 tanx＋ 1 tanx ＝ 2sin2 x 2－sinx＋1 sinx cosx＋ cosx sinx ＝sinxcosx(2－cosx－sinx)＝(－ 12 25 )×(2－ 1 5 )＝－ 108 125. [点评]　(1)在三角函数的变换求值中，已知 sinα＋cosα，sinαcosα，sinα－cosα(或 cosα－sinα)中的一个， 可利用方程的思想求出另外两个的值；(2)注意整体代入的思想方法． 跟踪练习 2： 已知 sinα，cosα 是关于 x 的二次方程 2x2＋( 2＋1)x＋m＝0 的两根，求 2tanα· cosα－sinα 1－tan2α 的值． [分析]　先将所给三角函数式化简，由方程的判别式Δ≥0，结合韦达定理求解． [解析]　2tanα· cosα－sinα 1－tan2α ＝ 2sinα cosα · cosα－sinα 1－ sin2α cos2α ＝ 2sinαcosα cosα＋sinα 由根与系数关系可得 sinα＋cosα＝－ 2＋1 2 且 m 2＝sinα·cosα＝ sinα＋cosα2－1 2 ＝ (－ 2＋1 2 )2－1 2 ＝ 2 2－1 8 ，所以 m＝ 2 2－1 4 . 故原式＝ 2 2－1 4 － 2＋1 2 ＝ 3 2－5 2 . 3.命题方向：利用诱导公式进行化简与求值 [例 3]　已知 f(α)＝ sinπ－αcos2π－αtan－α＋π －tan－α－πsin－π－α ； (1)化简 f(α)； (2)若 α 是第三象限角，且 cos(α－ 3π 2 )＝ 1 5，求 f(α)的值． [分析]　显然应用到诱导公式，可以直接从六组诱导公式中合理选用． [解析]　(1)f(α)＝ sinα·cosα·－tanα tanαsinα ＝－cosα. (2)∵cos(α－ 3π 2 )＝－sinα， ∴sinα＝－ 1 5，cosα＝－ 52－12 5 ＝－ 2 5 6， ∴f(α)＝ 2 5 6. [点评]　熟练应用诱导公式是解答本题的关键．诱导公式应用原则是：负化正、大化小、化到锐角为终了．(能求值 的要求出值) [例 4]　化简： tanπ－αcos2π－αsin(－α＋ 3π 2 ) cos－α－πsin－π－α [分析]　化简上式，要认真观察“角”，显然需利用诱导公式，注意诱导公式的合理选用． [解析]　解法 1： 原式＝ －tanα·cos[π＋(π－α)]·sin(π＋ π 2 －α) cos(π＋α)·[－sin(π＋α)] ＝ －tanα·[－cosπ－α]·[－sin(π 2 －α)] －cosα·sinα ＝ －tanα·cosα·－cosα －cosα·sinα ＝ －tanα·cosα sinα ＝－ sinα cosα· cosα sinα＝－1. 解法 2：原式＝ －tanα·cos－α·sin(－α－ π 2 ) cos(π－α)·sin(π－α) ＝ tanα·cosα·sin(α＋ π 2 ) －cosα·sinα ＝ sinα cosα·cosα －sinα ＝－1. [点评]　解决此类问题需合理运用诱导公式，用公式时需特别注意化简后函数的名称与符号，一定要细心计算，以免 出错． 跟踪练习 3： 化简： tan3π－α sinπ－αsin(3π 2 －α) ＋ sin2π－αcos(α－7π 2 ) sin(3π 2 ＋α)cos2π＋α [分析]　要认真观察“角”，运用诱导公式时特别注意函数名称与符号． [解析]　原式＝ tan－α sinα·－cosα＋ sin－α·cos(α＋ π 2 ) －cosα·cosα ＝ tanα sinα·cosα＋ －sinα·－sinα －cosα·cosα ＝ 1 cos2α－ sin2α cos2α＝ 1－sin2α cos2α ＝ cos2α cos2α＝1. 4.命题方向：三角函数公式在解三角形中的应用 [例 5]　在△ABC 中，若 sin(2π－A)＝－ 2sin(π－B)， 3cosA＝－ 2cos(π－B)，求△ABC 的三个内角． [分析]　由诱导公式可化简得到 sinA＝ 2sinB， 3cosA＝ 2cosB，进而由 sin2A＋cos2A＝1 可求出 A，进一 步即可求出 B 和 C. [解析]　由已知得 sinA＝ 2sinB， 3cosA＝ 2cosB，两式平方相加得 2cos2A＝1，cosA＝± 2 2 . 若 cosA＝－ 2 2 ，则 cosB＝－ 3 2 ， 此时，A，B 均为钝角，不可能， ∴cosA＝ 2 2 ，故 A＝ π 4 ， cosB＝ 3 2cosA＝ 3 2 ⇒B＝ π 6 ， C＝π－(A＋B)＝ 7π 12 . [点评]　1.诱导公式在三角形中经常应用，常用的变形结论有：A＋B＝π－C； 2A＋2B＋2C＝2π； A 2＋ B 2＋ C 2＝ π 2 . 2．求角时，一般先求出该角的某一三角函数值，再确定该角的范围，最后求角． 跟踪练习 4： 在锐角三角形 ABC 中，求证：sinA＋sinB＋sinC>cosA＋cosB＋cosC. [解析]　∵△ABC 是锐角三角形， ∴A＋B> π 2 ，即 π 2 >A> π 2 －B>0， ∴sinA>sin(π 2 －B)，即 sinA>cosB； 同理 sinB>cosC，sinC>cosA， ∴sinA＋sinB＋sinC>cosA＋cosB＋cosC. （五）思想方法点拨 1．计算任意角的三角函数值，主要是运用诱导公式化任意角三角函数为锐角三角函数，其一般步骤是： (1)负化正：当已知角为负角时，先利用－α的诱导公式把这个角的三角函数值化为正角的三角函数值； (2)正化主：当已知角是大于 360°的角时，可用 k·360°＋α 的诱导公式把这个角的三角函数值化为主区间(0°， 360°)上的角的三角函数值； (3)主化锐：当已知角是 90°到 360°间的角时，可利用 180°±α，360°－α的诱导公式把这个角的三角函数值化 为 0°到 90°间的角的三角函数值(对于非特殊角用查表或用计算器求出结果)． 2．已知角α的某一种三角函数值，求角α的其余三角函数值时，如果应用平方关系，就要进行分类讨论，先确定角 的终边所在的象限，再确定三角函数值的符号．要注意公式的合理选择和方法的灵活性． 3．在利用同角三角函数的基本关系化简、求值时，要注意用“是否是同角”来区分和选用公式． 4．在应用诱导公式进行三角式的化简、求值时，应注意公式中符号的选取．应用公式时把角α看成锐角，如果出现 kπ±α 的形式时，常对 k 值是奇数还是偶数进行分类讨论，以确定角所在的象限． 5．在进行三角函数化简和三角恒等式的证明时，细心观察题目的特征，灵活、恰当的选用公式，一般思路是将 切化弦，但在某些特殊问题中就不要化切为弦，只须利用倒数关系即可，否则解法较繁，如“求证 tanα－cotβ tanβ－cotα＝ tanαcotβ”，利用倒数关系可得简证． （六）课后强化作业 一、选择题 1．sin600°＋tan240°的值是(　　) A．－ 3 2 　　　　B. 3 2 C．－1 2＋ 3 D.1 2＋ 3 [答案]　B [解析]　sin600°＋tan240°＝sin240°＋tan240°＝sin(180°＋60°)＋tan(180°＋60°) ＝－sin60°＋tan60°＝－ 3 2 ＋ 3＝ 3 2 . 2．设 tan(5π＋α)＝m，则sin(α－3π)＋cos(π－α) sin(－α)－cos(π＋α) 的值为(　　) A.m＋1 m－1 B.m－1 m＋1 C．－1 D．1 [答案]　A [解析]　sin(α－3π)＋cos(π－α) sin(－α)－cos(π＋α) ＝sin(－4π＋π＋α)－cosα －sinα＋cosα ＝ －sinα－cosα －sinα＋cosα＝tanα＋1 tanα－1. 又 tan(5π＋α)＝m， ∴tanα＝m，∴原式＝m＋1 m－1. 3．若 sin2θ＝1 4且 θ∈( π 4，π 2 )，则 cosθ－sinθ 的值是(　　) A. 3 2 B.3 4 C．－ 3 2 D．－3 4 [答案]　C [解析]　(cosθ－sinθ)2＝1－sin2θ＝3 4， ∵π 4<θ<π 2，∴cosθ0，cosx<0，且|sinx|>|cosx|， ∴tanx<0 且|tanx|>1，故选 A. 5．已知 tanθ＝2，则 sin( π 2＋θ )－cos(π＋θ) sin( π 2－θ )－sin(π－θ) ＝(　　) A．2 B．－2 C．0 D.2 3 [答案]　B [解析]　 sin( π 2＋θ )－cos(π＋θ) sin( π 2－θ )－sin(π－θ) ＝cosθ＋cosθ cosθ－sinθ＝ 2 1－tanθ＝ 2 1－2＝－2. 6．已知 tan2α＝－2 2，且满足π 4<α<π 2，则 2cos2α 2－sinα－1 2sin(π 4＋α) 的值为(　　) A. 2 B．－ 2 C．－3＋2 2 D．3－2 2 [答案]　C [解析]　 2cos2α 2－sinα－1 2sin(π 4＋α) ＝cosα－sinα sinα＋cosα＝1－tanα tanα＋1. 又 tan2α＝－2 2＝ 2tanα 1－tan2α⇒2 2tan2α－2tanα－2 2＝0.解得 tanα＝－ 2 2 或 2. 又π 4<α<π 2，∴tanα＝ 2.原式＝1－ 2 2＋1 ＝－3＋2 2. 7．已知 cos( π 6－α )＝ 3 3 ，则 cos( 5 6π＋α)－sin2 (α－π 6 )的值是(　　) A.2＋ 3 2 B．－2＋ 3 2 C.2－ 3 3 D. －2＋ 3 3 [答案]　B [解析]　∵cos( 5 6π＋α)＝cos[π－( π 6－α )]＝－cos( π 6－α )＝－ 3 3 ， 而 sin2 (α－π 6 )＝1－cos2 (α－π 6 )＝1－1 3＝2 3， ∴原式＝－ 3 3 －2 3＝－2＋ 3 3 . 8．若 sinα＋cosα＝tanα(0 < α < π 2)，则 α 的取值范围是(　　) A.(0，π 6 ) B.( π 6，π 4 ) C.( π 4，π 3 ) D.( π 3，π 2 )[答案]　C [解析]　方法一：排除法． 在(0，π 4 )上，sinα＋cosα>1，而 tanα 在(0，π 4 )上小于 1，故排除答案 A、B；因为 sinα＋cosα≤ 2，而在( π 3，π 2 )上 tanα> 3，sinα＋cosα 与 tanα 不可能相等，故排除 D. 方法二：由 sinα＋cosα＝tanα，0<α<π 2， ∴tan2α＝1＋2sinαcosa＝1＋sin2α， ∵0<α<π 2，∴0<2α<π， ∴00， ∴10， d＝cos(－cos32°)＝cos(cos32°)>0， 又 00，cosα<0. (1)(sinα－cosα)2＝1－2sinα·cosα＝1－(－7 9 )＝16 9 ，∴sinα－cosα＝4 3. (2)sin3 ( π 2－α )＋cos3 ( π 2＋α )＝cos3α－sin3α ＝(cosα－sinα)(cos2α＋cosα·sinα＋sin2α) ＝－4 3×(1－ 7 18)＝－22 27. 13．已知 cos( π 2＋α )＝2sin(α－π 2 ).求 sin3(π－α)＋cos(α＋π) 5cos( 5π 2 －α)＋3sin( 7π 2 －α) 的值． [解析]　∵cos( π 2＋α )＝2sin(α－π 2 )， ∴－sinα＝－2sin( π 2－α )， ∴sinα＝2cosα，即 tanα＝2. ∴ sin3(π－α)＋cos(α＋π) 5cos( 5π 2 －α)＋3sin( 7π 2 －α) ＝ sin3α－cosα 5cos(2π＋π 2－α)＋3sin(4π－π 2－α) ＝ sin3α－cosα 5cos( π 2－α )－3sin( π 2＋α ) ＝ sin3α－cosα 5sinα－3cosα＝sin2α·tanα－1 5tanα－3 ＝2sin2α－1 10－3 ＝2sin2α－1 7 ＝2sin2α－(sin2α＋cos2α) 7(sin2α＋cos2α) ＝ sin2α－cos2α 7(sin2α＋cos2α)＝ tan2α－1 7(tan2α＋1)＝ 4－1 7 × (4＋1)＝ 3 35. 14．已知 sinθ，cosθ 是方程 x2－( 3－1)x＋m＝0 的两根． (1)求 m 的值； (2)求 sinθ 1－cosθ sinθ ＋ cosθ 1－tanθ的值． [解析]　(1)由韦达定理可得 Error!， 由①得 1＋2sinθ·cosθ＝4－2 3. 将②代入得 m＝3 2－ 3，满足 Δ＝( 3－1)2－4m≥0，故所求 m 的值为3 2－ 3. (2)先化简： sinθ 1－cosθ sinθ ＋ cosθ 1－tanθ＝ sinθ 1－cosθ sinθ ＋ cosθ 1－sinθ cosθ ＝ sin2θ sinθ－cosθ＋ cos2θ cosθ－sinθ＝cos2θ－sin2θ cosθ－sinθ ＝cosθ＋sinθ＝ 3－1. 15．已知 tanα 是方程 x2＋ 2 cosαx＋1＝0 的两个根中较小的根，求 α 的值． [解析]　∵tanα 是方程 x2＋ 2 cosαx＋1＝0 的较小根， ∴方程的较大根是 1 tanα.由根与系数的关系知 tanα＋ 1 tanα＝－ 2 cosα，即 1 sinαcosα＝－ 2 cosα ∴sinα＝－1 2. 解得 α＝2kπ＋7π 6 ，或 α＝2kπ－π 6，k∈Z. 当 α＝2kπ＋7π 6 (k∈Z)时，tanα＝ 3 3 ，cotα＝ 3； 当 α＝2kπ－π 6(k∈Z)时，tanα＝－ 3 3 ，cotα＝－ 3，不合题意．∴α＝2kπ＋7π 6 ，k∈Z.