- 2021-07-01 发布 |
- 37.5 KB |
- 5页
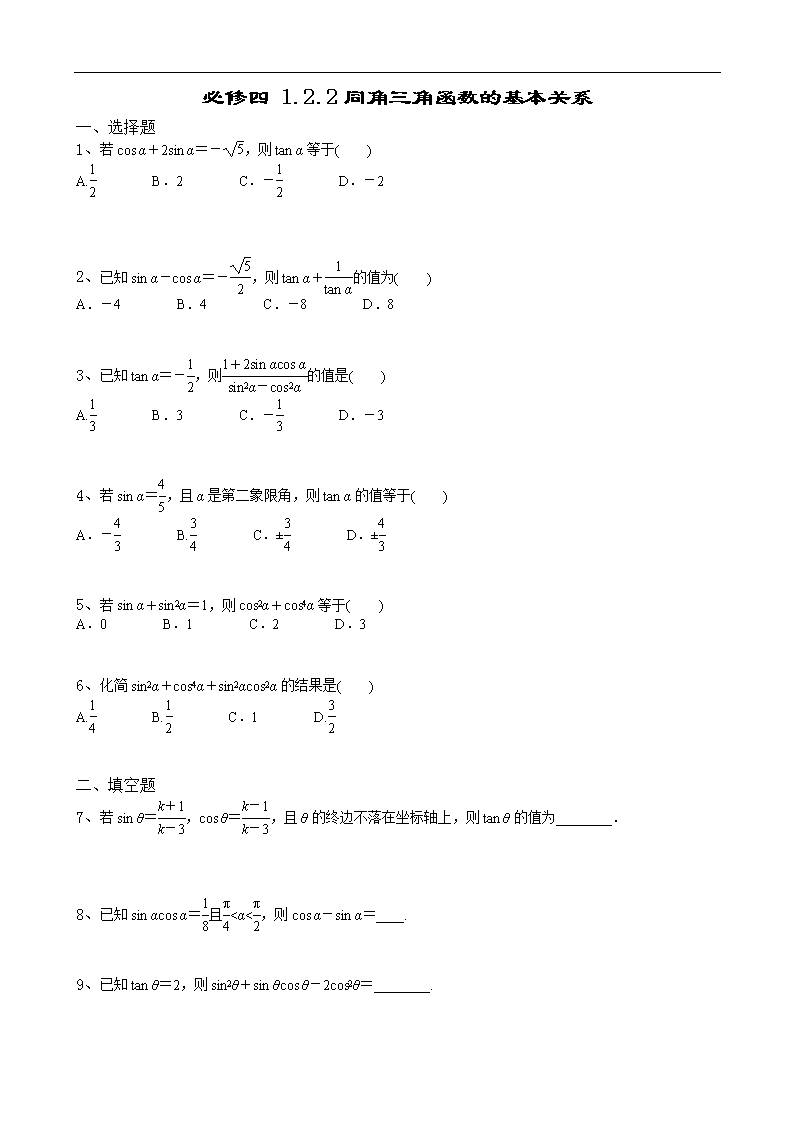


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修4同步练习:同角三角函数的基本关系
必修四 1.2.2同角三角函数的基本关系 一、选择题 1、若cos α+2sin α=-,则tan α等于( ) A. B.2 C.- D.-2 2、已知sin α-cos α=-,则tan α+的值为( ) A.-4 B.4 C.-8 D.8 3、已知tan α=-,则的值是( ) A. B.3 C.- D.-3 4、若sin α=,且α是第二象限角,则tan α的值等于( ) A.- B. C.± D.± 5、若sin α+sin2α=1,则cos2α+cos4α等于( ) A.0 B.1 C.2 D.3 6、化简sin2α+cos4α+sin2αcos2α的结果是( ) A. B. C.1 D. 二、填空题 7、若sin θ=,cos θ=,且θ的终边不落在坐标轴上,则tan θ的值为________. 8、已知sin αcos α=且<α<,则cos α-sin α=____. 9、已知tan θ=2,则sin2θ+sin θcos θ-2cos2θ=________. 10、已知α是第四象限角,tan α=-,则sin α=________. 三、解答题 11、已知sin θ、cos θ是关于x的方程x2-ax+a=0的两个根(a∈R). (1)求sin3θ+cos3θ的值; (2)求tan θ+的值. 12、证明: (1)-=sin α+cos α; (2)(2-cos2α)(2+tan2α)=(1+2tan2α)(2-sin2α). 13、求证:=. 14、化简:. 以下是答案 一、选择题 1、B [方法一 由联立消去cos α后得(--2sin α)2+sin2α=1. 化简得5sin2α+4sin α+4=0 ∴(sin α+2)2=0,∴sin α=-. ∴cos α=--2sin α=-. ∴tan α==2. 方法二 ∵cos α+2sin α=-, ∴cos2α+4sin αcos α+4sin2α=5, ∴=5, ∴=5, ∴tan2α-4tan α+4=0, ∴(tan α-2)2=0,∴tan α=2.] 2、C [tan α+=+=. ∵sin αcos α==-,∴tan α+=-8.] 3、C [=====-.] 4、A 5、B 6、C 二、填空题 7、 解析 ∵sin2θ+cos2θ=2+2=1, ∴k2+6k-7=0, ∴k1=1或k2=-7. 当k=1时,cos θ不符合,舍去. 当k=-7时,sin θ=,cos θ=,tan θ=. 8、- 解析 (cos α-sin α)2=1-2sin αcos α=, ∵<α<,∴cos α查看更多
相关文章
- 当前文档收益归属上传用户