数学理卷·2018届重庆市合川大石中学高二上学期第一次月考（2016-10）

数学理卷·2018届重庆市合川大石中学高二上学期第一次月考（2016-10）

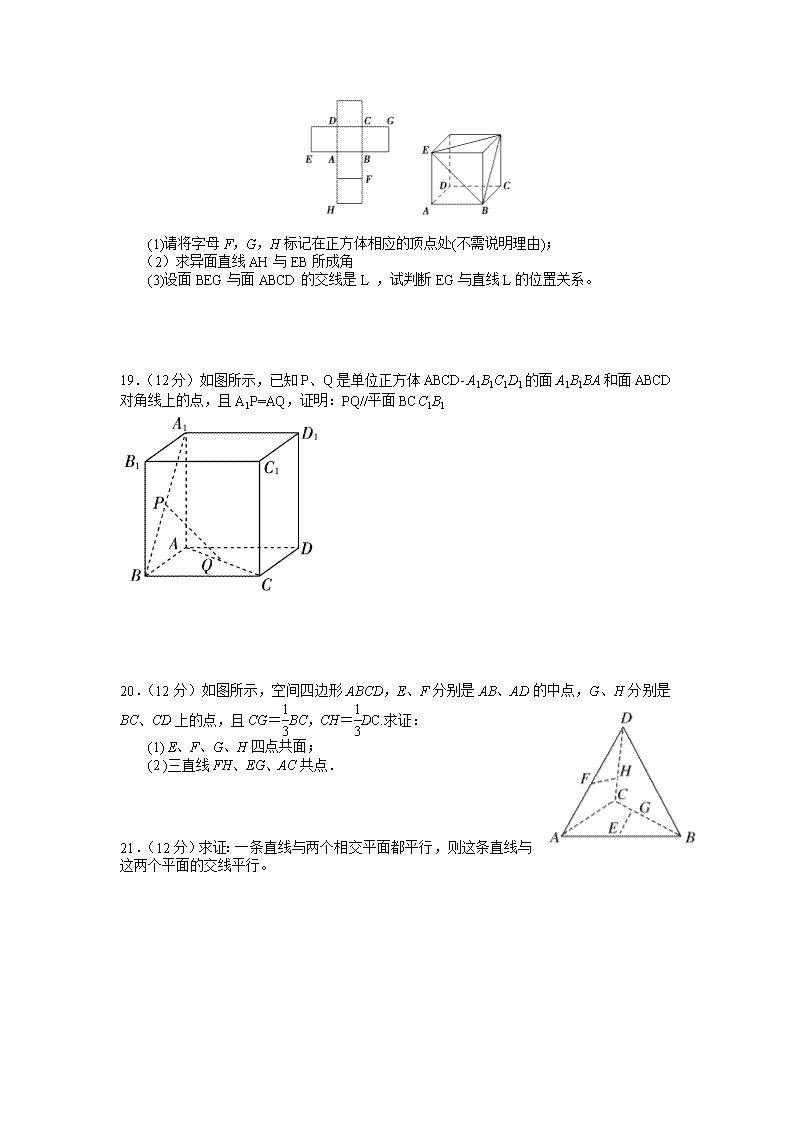
重庆市合川大石中学高2018级１６年秋期第一次月考 数学试卷（理科）‎ ‎ 　　　　满分：150分 时间：120分钟 一、选择题（5×12=60）‎ ‎1．一几何体的直观图如图，下列给出的四个俯视图中正确的是(　　)‎ ‎2．下列推理错误的是(　　)‎ A．A∈l，A∈α，B∈l，B∈α⇒lα B．A∈α，A∈β，B∈α，B∈β⇒α∩β＝AB C．lα，A∈l⇒A∉α D．A∈l，lα⇒A∈α ‎3．若某几何体的三视图如图所示，则这个几何体的直观图可以是(　　)‎ ‎ ‎ ‎ A 　B C D ‎4．已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为(　　)‎ ‎5．下列四个结论中正确的个数为(　　)‎ ‎①两条不同的直线都和同一个平面平行，则这两条直线平行.‎ ‎②两条不同直线都和第三条直线垂直，则这两条直线平行.‎ ‎③‎ ‎④若 ‎ 　 A．0 B．‎1 ‎C．2 D．3‎ ‎6．某几何体的三视图如图所示，则该几何体的体积为 (　　)‎ A．＋ B．1＋ C．＋ D．1＋ ‎7．如图，正方体ABCDA1B‎1C1D1中，E、F分别为棱AB，CC1的中点,在平面ADD‎1A1内且与平面D1EF平行的直线(　　)‎ A．不存在 ‎ B．有1条 C．有2条 ‎ D．有无数条 ‎8．在正方体ABCD－A1B‎1C1D1中，M和N分别为A1B1和B‎1C1的中点，那么直线AM与CN所成角的余弦值是 （ ）‎ A． B． C． D． ‎ ‎9．设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.可以填入的条件有(　　)‎ ‎ A．①② 　 B．②③　　 C．①③ 　 D．①②③‎ ‎10．某三棱锥的三视图如图所示，则该三棱锥的表面积是（ ）‎ A． ‎ B． ‎ C． ‎ D．5‎ ‎11．圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为(　　)‎ A．120° B．150° C．180° D．240°‎ ‎12．已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O ABC体积的最大值为36，则球O的表面积为(　　)‎ A．36π B．64π C．144π D．256π 二、填空题（4×5=20）‎ ‎13．如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，‎ 其中O′A′＝6，O′C′＝2，则原图形OABC的面积为________．‎ ‎14．现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个。若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为 ‎ ‎15．高为4，底面边长为2的正四棱锥的内切球的体积为 ‎ ‎16．空间四边形ABCD中，AB＝CD且AB与CD所成的角为30°，‎ E、F分别为BC、AD的中点，则EF与AB所成角的大小为 ．‎ 三、解答题（共70分）‎ ‎17．（10分）如图所示，在三棱柱ABCA1B‎1C1中，E，F，G，H分别是AB，AC，A1B1，A‎1C1的中点，‎ 求证：(1)GH∥面ABC ‎(2)平面EFA1∥平面BCHG.‎ ‎18．（12分）一个正方体的平面展开图及该正方体的直观图的示意图如图所示．‎ ‎(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；‎ ‎（2）求异面直线AH与EB所成角 ‎(3)设面BEG与面ABCD的交线是L ，试判断EG与直线L的位置关系。‎ ‎19．（12分）如图所示，已知P、Q是单位正方体ABCD-A1B‎1C1D1的面A1B1BA和面ABCD对角线上的点，且A1P=AQ，证明：PQ//平面BCC1B1‎ ‎20．（12分）如图所示，空间四边形ABCD，E、F分别是AB、AD的中点，G、H分别是BC、CD上的点，且CG＝BC，CH＝DC.求证：‎ ‎(1) E、F、G、H四点共面；‎ ‎(2 )三直线FH、EG、AC共点．‎ ‎21．（12分）求证：一条直线与两个相交平面都平行，则这条直线与这两个平面的交线平行。‎ ‎22．（12分）（1）如图所示，四边形EFGH为空间四边形ABCD的一个截面，若ＣＤ∥面EFGH，求证：ＥＨ∥ＦＧ ‎（2）如图所示，在底面是平行四边形的四棱锥P－ABCD中，点E在PD上，且PE∶ED＝2∶1，在棱PD上是否存在一点F，使BF∥平面AEC？并证明你的结论．‎ ‎ ‎