专题05+线性规划（第01期）-2018年高考数学（理）备考之百强校小题精练系列

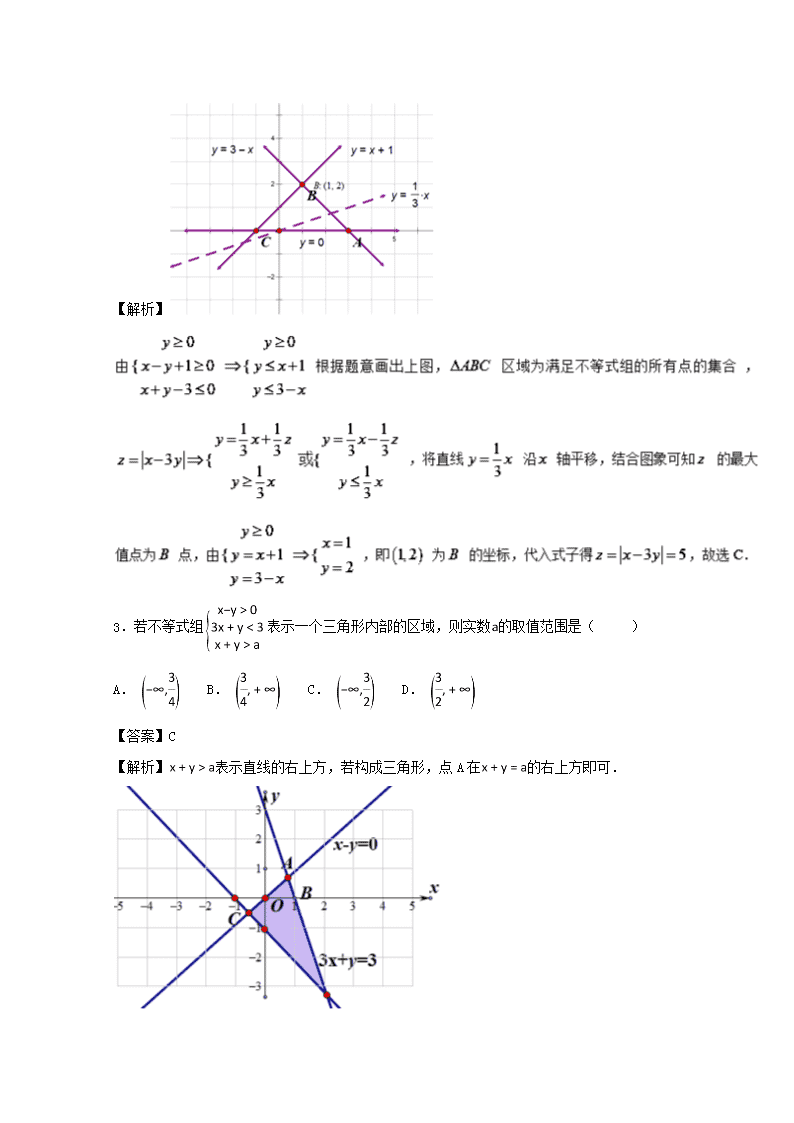
专题05+线性规划（第01期）-2018年高考数学（理）备考之百强校小题精练系列

‎2018届高考数学（理）小题精练 专题05 线性规划 ‎1．若直线上存在点满足约束条件则实数的最大值为（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】如图，当直线经过函数的图象 点睛：直线上存在点满足约束条件，即直线和可行域有公共区域．‎ ‎2．设满足约束条件，则的最大值为（ ）‎ A． 1 B． 3 C． 5 D． 6‎ ‎【答案】C ‎【解析】‎ ‎3．若不等式组表示一个三角形内部的区域，则实数的取值范围是（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】表示直线的右上方，若构成三角形，点A在的右上方即可．‎ 又，所以，即．故选C 点睛：本题考查的是线性规划问题，解决线性规划问题的实质是把代数问题几何化，即数形结合思想．需要注意的是：一，准确无误地作出可行域;二，画目标函数所对应的直线时，要注意让其斜率与约束条件中的直线的斜率进行比较，避免出错;三，一般情况下，目标函数的最大值或最小值会在可行域的端点或边界上取得．‎ ‎4．设实数满足 , 则 的取值范围为（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】画出可行域如图所示：‎ 点睛：本题是线性规划的综合应用，考查的是非线性目标函数的最值的求法．解决这类问题的关键是利用数形结合的思想方法，给目标函数赋于一定的几何意义．‎ ‎5．设满足约束条件 ，则的最大值为（ ）‎ A． 1024 B． 256 C． 8 D． 4‎ ‎【答案】B ‎【解析】由，令u=2x−y，作出约束条件 ,对应的平面区域如图(阴影部分):‎ 平移直线y=2x−u 点睛：含有实际背景的线性规划问题其解题关键是找到制约求解目标的两个变量，用这两个变量建立可行域和目标函数，在解题时要注意题目中的各种相互制约关系，列出全面的制约条件和正确的目标函数．‎ ‎6．若变量满足条件，则的最小值是（ ）‎ A． 13 B． 18 C． 20 D． 26‎ ‎【答案】B ‎【解析】目标函数表示点 到 的距离的平方，画出可行域，由图象知道点 到的距离最小， ，==18． ‎ ‎7．若，且当时，恒有，则以为坐标点所形成的平面区域的面积等于（ ）‎ A． B． 1 C． D． ‎ ‎【答案】B ‎【解析】令 恒成立， ‎ ‎8．已知满足约束条件，且的最大值是最小值的3倍，则的值是（ ）‎ A． B． C．7 D．不存在 ‎【答案】A ‎【解析】‎ 试题分析：由题意得，作出不等式组对应的平面区域，由得 ‎，平移直线由图象可知，当直线经过点（直线和的交点），此时最大，为，当直线经过点（直线和的交点）时，最小，为，又因为的最大值是最小值的倍，故，故选A．‎ 考点：线性归划最值问题．‎ ‎9．设，在约束条件下，目标函数的最大值小于，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】‎ 考点：线性规划．‎ ‎10．已知实数满足，若目标函数的最大值为，最小值为，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】‎ 考点：线性规划．‎ ‎11．设满足约束条件，则 的最大值为________．‎ ‎【答案】‎ ‎【解析】不等式组表示的平面区域如图阴影所示，‎ 点睛：线性规划中，目标函数是两点间的距离，做这类型题一定要处理好目标函数，分清目标函数符合什么样的几何意义．‎ ‎12．已知实数， 满足则的取值范围为__________．‎ ‎【答案】‎ ‎【解析】作出可行域:‎ 观察可知： ，易得： ,故，‎ 故答案为： ‎ 点睛：本题考查的是线性规划问题，解决线性规划问题的实质是把代数问题几何化，即数形结合思想．需要注意的是：一，准确无误地作出可行域;二，画目标函数所对应的直线时，要注意让其斜率与约束条件中的直线的斜率进行比较，避免出错;三，一般情况下，目标函数的最大值或最小值会在可行域的端点或边界上取得．‎