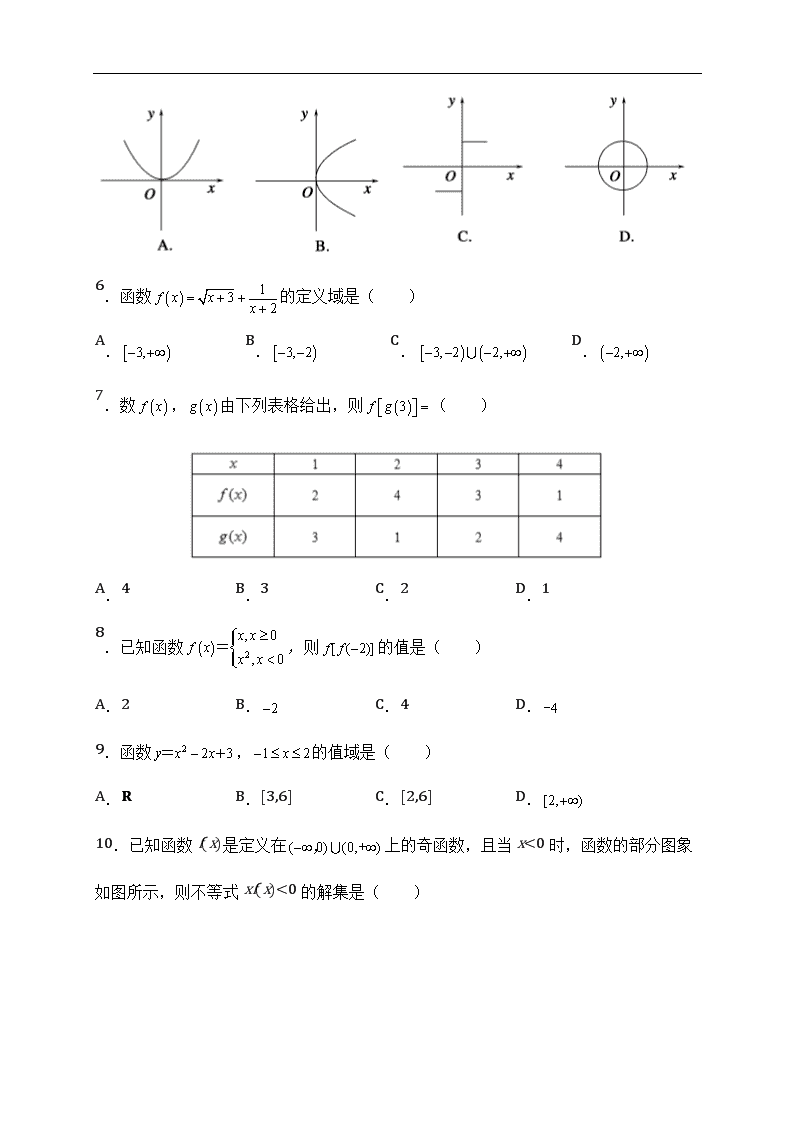四川省眉山市东坡区多悦高级中学校2020-2021学年高一上学期期中考试数学试题
多悦高中 2023 届半期考试
数 学 试题
一、选择题(本大题共 12 个小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项
是符合题目要求的)
1
.已知集合 1,0,1A , 2,0,2B ,则集合 A B ( )
A
.
0 B
.
C
. 0
D
. 1
2
.设全集
U
=
R
,集合 2 2{ | }M y y x x U= = + , ,集合 3{ | }N y y x x U= = , ,则 M N 等于
( )
A
.
{1,3,2,6} B
.
{(1,3)
,
(2,6)} C
.
M D
.
{3,6}
3
.如图所示,阴影部分表示的集合是( )
A
. ABCU
B
. BACU
C
. BACU
D
. BACU
4
.设全集
U
{x|0
0x x
f x f x
,
则( )
A
. 5( )f
a}
,
U
=
R
.
(
1
)求
A∪B
, BACU ;
(
2
)若 A C ,求
a
的取值范围.
18
.(
12
分)设
A
=
{x|x
2
2(a
1)x
a
2
1
=
0}
, { | ( 02) 14B x x x x
= + = ,
x∈Z}
.
若
A∩B
=
A
,求
a
的取值范围.
19
.(
12
分)已知函数
f(x)
=
2x
m
,其中
m
为常数.
(
1
)求证:函数
f(x)
在
R
上是减函数;
(
2
)当函数
f(x)
是奇函数时,求实数
m
的值.
20
.(
12
分)已知函数
f(x)
是正比例函数,函数
g(x)
是反比例函数,且
f(1)
=
1
,
g(1)=
2
,
(
1
)求函数
f(x)
和
g(x)
;
(
2
)判断函数
f(x)
g(x)
的奇偶性
.
21.
(
12
分)经过市场调查,超市中的某种小商品在过去的近
40
天的日销售量(单位:
件)与价格(单位:元)为时间t(单位:天)的函数,且日销售量近似满足 100 2g t t ,
价格近似满足 40 20f t t .
(1)
写出该商品的日销售额 y (单位:元)与时间t (0 40t )的函数解析式并用分段
函数形式表示该解析式(日销售额
=
销售量商品价格);
(2)
求该种商品的日销售额 y 的最大值和最小值
.
22
.(
12
分)函数
f(x)
= 21
ax b
x
是定义在 1,1 上的奇函数,且 1 2
2 5f
.
(
1
)求
f(x)
的解析式;
(
2
)证明
f(x)
在 1,1 上为增函数;
(
3
)解不等式
f(t
1)
f(t)<0
.
1
多悦高中 2023 届第一期半期考试
数 学 答 案
一、选择题
1.【答案】C
【解析】因为集合 1,0,1A , 2,0,2B ,所以 0A B ,故选 C.
2.【答案】C
【解析】 ,[ )2M = + ,N=R..故选 C.
3.【答案】A
【解析】因为阴影部分既在集合 U Bð 中又在集合 A 中,
所以阴影部分为 U B Að ,故选 A.
4.【答案】A
【解析】可借助 Venn 图(如图 2)解决,数形结合.故选 A.
图 2
5.【答案】A
【解析】根据函数的概念知,只有“一对一”或“多对一”对应才能构成函数关系.
故选 A.
6.【答案】C
2
【解析】由题可得: 3 0 32 0
x xx
且 2x ,故选 C.
7.【答案】A
【解析】由表可知 3 2g , 3 2 4f g f ,故选 A.
8.【答案】C
【解析】∵ 2x=- ,而 2 0 ,∴ 2( ) (2 2 4)f = = .
又 4>0,∴ [ ( )2 4 4]f f f .故选 C.
9.【答案】C
【解析】画出函数 2 2 3y x x= + , 1 2x 的图象,如图 3 所示,观察函数的图象可得图象上所有
点的纵坐标的取值范围是[2,6],所以值域是[2,6].故选 C.
10.【答案】D
【解析】xf(x)<0
⇔
x 与 f(x)异号,由函数图象及奇偶性易得结论.故选 D.
11.【答案】B
【解析】∵f(x)是偶函数,∴f(x)的图象关于 y 轴对称.
∴f(x)在[ ]7,0 上是减函数,且最大值为 6.故选 B.
12.【答案】C
【解析】∵对任意 1 2 ( , ]0x x , (x1≠x2),都有 2 1
2 1
>0x x
f x f x
,
∴对任意 1 2 ( , ]0x x , ,若 x18}.∴ U A Bð ={x|10.∴f(x1)>f(x2)
5
∴函数 f(x)在 R 上是减函数.
(2)∵函数 f(x)是奇函数,
∴对任意 x∈R,有 f( x)= f(x).
∴2x m= ( 2x m).∴m=0.
20.【答案】(1)f(x)=x,g(x)= 2
x
;(2)奇函数.
【解析】(1)设 1f x k x= ,g(x)= 2k
x
,其中 k1k2≠0.
∵f(1)=1,g(1)=2,∴ 1 1 1k = , 2 21
k .
∴k1=1,k2=2.∴f(x)=x,g(x)= 2
x
.
(2)设 h(x)=f(x) g(x),则 2h x x x
= ,
∴函数 h(x)的定义域是 0,,0 .
∵h( x)= x 2
x
= 2x x
= h(x),
∴函数 h(x)是奇函数,即函数 f(x) g(x)是奇函数.
21.【答案】(1)由题意知 • 100 2 40 20y g t f t t t
100 2 20 ,0 20
100 2 60 ,20 40
t t ty t t t
.
(2)当 20 40t 时, 100 2 60y t t 在区间 20,40 上单调递减,故 400,2400y ;
当 0 20t 时, 100 2 20y t t 在区间 0,15 上单调递增,在区间 15,20 上单调递减,故
2000,2450y
当 40t 时, y 取最小值 400 ,当 15t 时, y 取最大值 2450 .
6
22.【答案】(1)f(x)=
21
x
x
;(2)见解析;(3) 1t|00,
所以 f(x1) f(x2)<0,故 f(x)在 1,1 上是增函数.
(3)因为 f(x)是奇函数,所以由 f(t 1)+f(t)<0,得 f(t 1)< f(t)=f( t).
由(2)知,f(x)在 1,1 上是增函数,
所以 1
查看更多