2018届二轮复习与线性规划有关的问题探究学案（江苏专用）

2018届二轮复习与线性规划有关的问题探究学案（江苏专用）

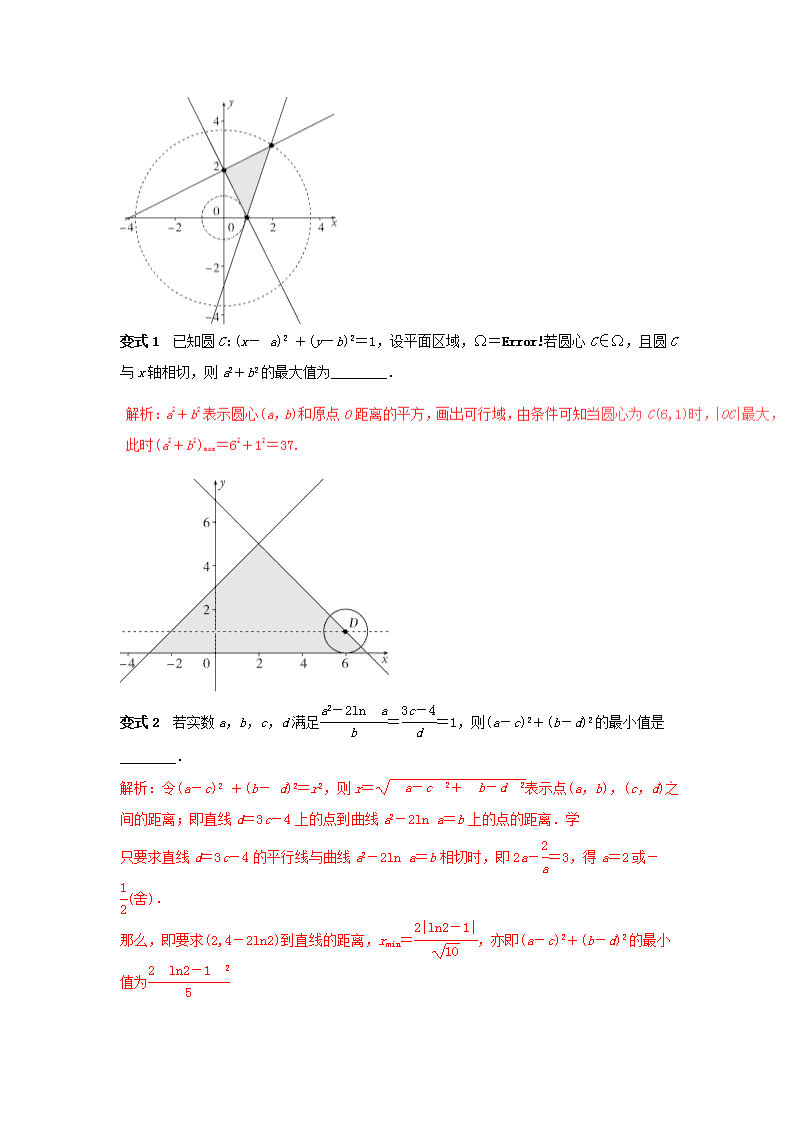
‎【热身训练】‎ ‎1. 已知实数x，y满足条件，则z＝2x＋y的最小值是________．‎ ‎2. 实数x，y满足约束条件若z＝y－ax取得最大值的最优解不唯一，则实数a的值为________．‎ 解析：作出约束条件如右图，将z＝y－ax化成斜截式y＝ax＋z，要使取得最优解不唯一，则y＝ax＋z在平移过程中与x＋y－2＝0重合，或2x－y＋2＝0重合，所以可知a等于2或－1.‎ ‎ ‎ ‎3. 设x，y满足约束条件且z＝x＋ay的最小值为7，则a＝________.‎ ‎4. 在平面直角坐标系xOy中，记不等式组表示的平面区域为D.若对数函数y＝logax(a>1)的图象与D有公共点，则实数a的取值范围是________．‎ 解析：作出不等式组表示的平面区域如图所示，若a>1，当对数函数的图象经过点A时，满足条件，此时解得即A(2,3)，则loga2＝3，解得a＝，‎ 所以当10，那么z＝10－3x－4y.令x＝rcos θ，y＝rsin θ，其中r∈[0,1]，则z＝10－3rcos θ－4rsin θ＝10－5rsin(θ＋φ)≤15.‎ 变式1　若对圆M：(x－1)2＋(y－1)2＝1上任意一点P(x，y)，|3x－4y＋a|＋|3x－4y－9|的取值与x，y无关，则实数a的取值范围是________．‎ 解析：设点P(x，y)为 那么，|3x－4y－9|＝|3cos θ－4sin θ－10|＝|10－5sin(θ＋φ)|≥5. ‎ 则由题意可知|3x－4y－9|＝9－3x＋4y，|3x－4y＋a|＝3x－4y＋a，即3x－4y＋a≥0，得a≥4y－3x＝1＋5sin(θ＋φ)，可知a≥6.学 ‎ 变式2　在平面直角坐标系xOy中，点集K＝{(x，y)|(|x|＋|3y|－6)(|3x|＋|y|－6)≤0}所对应的平面区域的面积为________．‎ 解析：当(x，y)在第一象限时，(x＋3y－ 6)(3x＋y－6)≤0，如图示，面积为6；由对称性可知，平面区域的面积为24.‎ ‎【乘热打铁】‎ ‎1．若点P(x，y)满足(x＋2y－1)(x－y＋3)≥0，则点P到原点的最短距离为________．‎ 解析：(x＋2y－1)(x－y＋3)≤0⇔或；作出可行域图象，即可知dmin＝＝.‎ ‎2. 设实数x，y满足，则u＝的取值范围是________．‎ 解析：u＝＝－；令k＝，则u＝k－，下只要求k的范围即可：由可行域易知k∈，那么u∈.‎ ‎3. 已知△ABC的三边长a，b，c，满足 b＋c≤2a，a＋c≤2b，求的取值范围．‎ 解析：由题得，令x＝，y＝，则上述不等式组可化为作出可行域得

查看更多