【数学】2019届一轮复习人教A版(文)第一章第2节命题及其关系、充分条件与必要条件学案
第二节命题及其关系、充分条件与必要条件
1.命题的概念
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
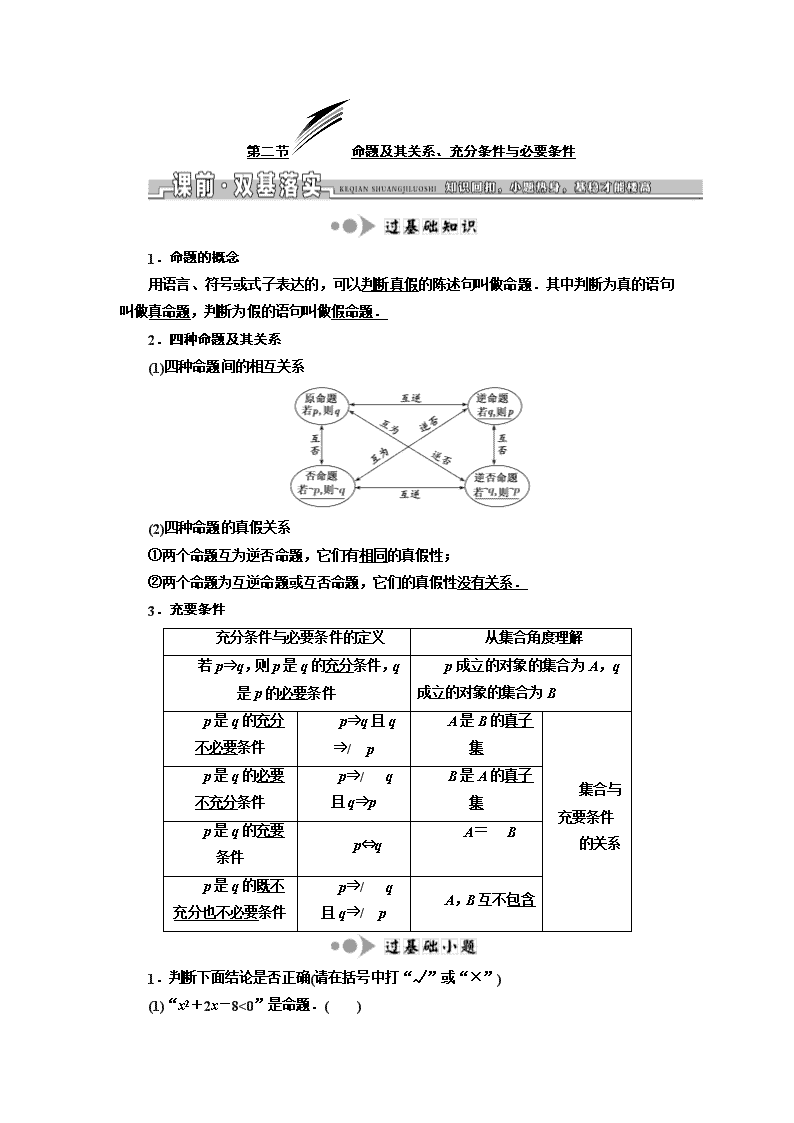
2.四种命题及其关系
(1)四种命题间的相互关系
(2)四种命题的真假关系
①两个命题互为逆否命题,它们有相同的真假性;
②两个命题为互逆命题或互否命题,它们的真假性没有关系.
3.充要条件
充分条件与必要条件的定义
从集合角度理解
若p⇒q,则p是q的充分条件,q是p的必要条件
p成立的对象的集合为A,q成立的对象的集合为B
p是q的充分不必要条件
p⇒q且qp
A是B的真子集
集合与充要条件
的关系
p是q的必要不充分条件
p q且q⇒p
B是A的真子集
p是q的充要条件
p⇔q
AB
p是q的既不充分也不必要条件
p q且qp
A,B互不包含
1.判断下面结论是否正确(请在括号中打“√”或“×”)
(1)“x2+2x-8<0”是命题.( )
(2)一个命题非真即假.( )
(3)四种形式的命题中,真命题的个数为0或2或4.( )
(4)命题“若p,则q”的否命题是“若p,则綈q”.( )
(5)若p是q成立的充分条件,则q是p成立的必要条件.( )
答案:(1)× (2)√ (3)√ (4)× (5)√
2.命题“若a>b,则a+c>b+c”的否命题是( )
A.若a≤b,则a+c≤b+c
B.若a+c≤b+c,则a≤b
C.若a+c>b+c,则a>b
D.若a>b,则a+c≤b+c
解析:选A 命题的否命题是将原命题的条件和结论均否定,所以题中命题的否命题为“若a≤b,则a+c≤b+c”.
3.在△ABC中,“A>B”是“sin A>sin B”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选C 由正弦定理知==2R(R为△ABC外接圆半径).若sin A>sin B,则>,即a>b,所以A>B;若A>B,则a>b,所以2Rsin A>2Rsin B,即sin A>sin B,所以“A>B”是“sin A>sin B”成立的充要条件.
4.(2018·唐山一模)若x∈R,则“x>1”是“<1”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选A 当x>1时,<1成立,而当<1时,x>1或x<0,所以“x>1”是“<1”的充分不必要条件,选A.
5.“若a
0,所以两边同除以c2,得a1,若x>0,则ax>1”的否命题为( )
A.已知00,则ax>1
B.已知a>1,若x≤0,则ax>1
C.已知a>1,若x≤0,则ax≤1
D.已知01”是大前提,在四种命题中不能改变;“x>0”是条件,“ax>1”是结论.由于命题“若p,则q”的否命题为“若綈p,则綈q”,故该命题的否命题为“已知a>1,若x≤0,则ax≤1”.故选C.
[怎样快解·准解]
1.判断命题真假的2种方法
(1)直接判断:判断一个命题是真命题,需经过严格的推理证明;而要说明它是假命题,只需举一反例即可.(如第2题逆命题的真假判断)
(2)间接判断(等价转化):由于原命题与其逆否命题为等价命题,如果原命题的真假不易直接判断,那么可以利用这种等价性间接地判断命题的真假.(如第2题原命题的真假判断)
2.谨防3类失误
(1)如果原命题是“若p,则q”,则否命题是“若綈p,则綈q”,而命题的否定是“若p,则綈q”,即否命题是对原命题的条件和结论同时否定,命题的否定仅仅否定原命题的结论(条件不变).
(2)对于不是“若p,则q”形式的命题,需先改写.(如第1题)
(3)当命题有大前提时,写其他三种命题时需保留大前提.(如第3题)
充分条件、必要条件以其独特的表达形式成为高考命题的热点.高考主要考查充分条件、必要条件的判断,常以选择题的形式出现,难度不大,属于基础题.,充分条件、必要条件作为一个重要载体,考查的数学知识面较广,几乎涉及数学知识各个方面.
[典题领悟]
1.(2017·北京高考)设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:选A ∵m=λn,∴m·n=λn·n=λ|n|2.
∴当λ<0,n≠0时,m·n<0.
反之,由m·n=|m||n|cos〈m,n〉<0⇔cos〈m,n〉<0⇔〈m,n〉∈,当〈m,n〉∈时,m,n不共线.
故“存在负数λ,使得m=λn”是“m·n<0”的充分而不必要条件.
2.(2017·天津高考)设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选B 由2-x≥0,得x≤2,
由|x-1|≤1,得0≤x≤2.
∵0≤x≤2⇒x≤2,x≤2⇒/ 0≤x≤2,
故“2-x≥0”是“|x-1|≤1”的必要而不充分条件.
3.已知条件p:x+y≠-2,条件q:x,y不都是-1,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选A 因为p:x+y≠-2,q:x≠-1,或y≠-1,
所以綈p:x+y=-2,綈q:x=-1,且y=-1,
因为綈q⇒綈p但綈p綈q,所以綈q是綈p的充分不必要条件,即p是q的充分不必要条件.
4.(2018·江西鹰潭中学月考)设f(x)=x2-4x(x∈R),则f(x)>0的一个必要不充分条件是( )
A.x<0 B.x<0或x>4
C.|x-1|>1 D.|x-2|>3
解析:选C 依题意,f(x)>0⇔x2-4x>0⇔x<0或x>4.又|x-1|>1⇔x-1<-1或x-1>1,即x<0或x>2,而{x|x<0或x>4}?{x|x<0或x>2},因此选C.
[解题师说]
1.熟记判断充分、必要条件的3种方法
方法
解读
适合题型
定义法
第一步,分清条件和结论:分清谁是条件,谁是结论;第二步,找推式:判断“p⇒q”及“q⇒p”的真假;第三步,下结论:根据推式及定义下结论
定义法是判断充分、必要条件最根本、最适用的方法.(如典题领悟第1题)
利用p⇒q与綈q⇒綈p;q⇒p与
适用于“
等价法
綈p⇒綈q;p⇔q与綈q⇔綈p的等价关系
直接正面判断不方便”的情况,可将命题转化为另一个等价的又便于判断真假的命题,再去判断.常用的是逆否等价法.(如典题领悟第3题)
集合法
记条件p,q对应的集合分别为A,B.若A?B,则p是q的充分不必要条件;若A?B,则p是q的必要不充分条件;若A=B,则p是q的充要条件
适用于“当所要判断的命题与方程的根、不等式的解集以及集合有关,或所描述的对象可以用集合表示时”的情况.(如典题领悟第2题及第4题)
2.把握探求某结论成立的充分、必要条件的3个方面
(1)准确化简条件,也就是求出每个条件对应的充要条件;
(2)注意问题的形式,看清“p是q的……”还是“p的……是q”,如果是第二种形式,要先转化为第一种形式,再判断;
(3)灵活利用各种方法判断两个条件之间的关系,充分、必要条件的判断常通过“⇒”来进行,即转化为两个命题关系的判断,当较难判断时,可借助两个集合之间的关系来判断.
[冲关演练]
1.(2018·安徽两校阶段性测试)设a∈R,则“a=4”是“直线l1:ax+8y-8=0与直线l2:2x+ay-a=0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选D ∵当a≠0时,==⇒直线l1与直线l2重合,∴无论a取何值,直线l1与直线l2均不可能平行,当a=4时,l1与l2重合.故选D.
2.对于直线m,n和平面α,β,m⊥α成立的一个充分条件是( )
A.m⊥n,n∥α B.m∥β,β⊥α
C.m⊥β,n⊥β,n⊥α D.m⊥n,n⊥β,β⊥α
解析:选C 对于选项C,因为m⊥β,n⊥β,所以m∥n,又n⊥α,所以m⊥α,故选C.
3.(2018·湖南湘中名校联考)“log2(2x-3)<1”是“4x>8”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选A 由log2(2x-3)<1⇒0<2x-3<2⇒8⇒2x>3⇒x>,所以“log2(2x-3)<1”是“4x>8”的充分不必要条件,故选A.
根据充分条件、必要条件求参数的范围是对充分条件、必要条件与集合之间关系的深层次考查.关键是合理转化条件,熟练掌握函数的有关性质、不等式的解法等知识,在近几年的高考题中出现频率较低,但也要引起关注.
[典题领悟]
1.(2018·保定模拟)已知集合A=,x∈,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,则实数m的取值范围是________.
解析:y=x2-x+1=2+,
∵x∈,∴≤y≤2,∴A=.
由x+m2≥1,得x≥1-m2,
∴B={x|x≥1-m2}.
∵“x∈A”是“x∈B”的充分条件,
∴A⊆B,∴1-m2≤,解得m≥或m≤-,
故实数m的取值范围是∪.
答案:∪
2.(2018·石家庄模拟)已知p:≤2,q:x2-2x+1-m2≤0(m>0),且綈p是綈q的必要不充分条件,则实数m的取值范围是________.
解析:法一:由≤2,得-2≤x≤10,
∴綈p对应的集合为{x|x>10或x<-2},
设A={x|x>10或x<-2}.
由x2-2x+1-m2≤0(m>0),得1-m≤x≤1+m(m>0),
∴綈q对应的集合为{x|x>1+m或x<1-m,m>0},
设B={x|x>1+m或x<1-m,m>0}.
∵綈p是綈q的必要不充分条件,
∴B?A,∴或解得m≥9,
∴实数m的取值范围为[9,+∞).
法二:∵綈p是綈q的必要不充分条件,
∴q是p的必要不充分条件.
即p是q的充分不必要条件,
由x2-2x+1-m2≤0(m>0),得1-m≤x≤1+m(m>0).
∴q对应的集合为{x|1-m≤x≤1+m,m>0},
设M={x|1-m≤x≤1+m,m>0},
又由≤2,得-2≤x≤10,
∴p对应的集合为{x|-2≤x≤10},
设N={x|-2≤x≤10}.
由p是q的充分不必要条件知,N?M,
∴或解得m≥9.
∴实数m的取值范围为[9,+∞).
答案:[9,+∞)
[解题师说]
1.解题“2关键”
(1)把充分、必要条件转化为集合之间关系.
(2)根据集合之间关系列出关于参数的不等式(组)求解.
2.解题“1注意”
求解参数的取值范围时,一定要注意区间端点值的检验,尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.(如典题领悟第2题)
[冲关演练]
1.(2017·湖北新联考四模)若x>2m2-3是-12m2-3是-10,q:x>a2-2a-2,若綈p是綈q的充分不必要条件,则实数a的取值范围是( )
A.[-1,+∞) B.[3,+∞)
C.(-∞,-1]∪[3,+∞) D.[-1,3]
解析:选C 由p:(x+3)(x-1)>0,解得x<-3或x>1,要使得綈p是綈q的充分不必要条件,则q是p的充分不必要条件,即q⇒p,p⇒/ q.所以a2-2a-2≥1,解得a≤-1或a≥3,故选C.
(一)普通高中适用作业
A级——基础小题练熟练快
1.命题“若一个数是负数,则它的平方是正数”的逆命题是( )
A.“若一个数是负数,则它的平方不是正数”
B.“若一个数的平方是正数,则它是负数”
C.“若一个数不是负数,则它的平方不是正数”
D.“若一个数的平方不是正数,则它不是负数”
解析:选B 依题意得,原命题的逆命题是“若一个数的平方是正数,则它是负数”.
2.设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选A 当四边形ABCD为菱形时,必有对角线互相垂直,即AC⊥BD;当四边形ABCD中AC⊥BD时,四边形ABCD不一定是菱形,还需要AC与BD互相平分.综上知,“四边形ABCD为菱形”是“AC⊥BD”的充分不必要条件.
3.命题“若x2+3x-4=0,则x=4”的逆否命题及其真假性为( )
A.“若x=4,则x2+3x-4=0”为真命题
B.“若x≠4,则x2+3x-4≠0”为真命题
C.“若x≠4,则x2+3x-4≠0”为假命题
D.“若x=4,则x2+3x-4=0”为假命题
解析:选C 根据逆否命题的定义可以排除A、D,因为x2+3x-4=0,所以x=-4或1,故原命题为假命题,即逆否命题为假命题.
4.设U为全集,A,B是集合,则“存在集合C,使得A⊆C,B⊆∁UC”是“A∩B=∅”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选C 依题意,若A⊆C,则∁U C⊆∁UA,若B⊆∁UC,可得A∩B=∅;若A∩B=∅,不妨令C=A,显然满足A⊆C,B⊆∁UC,故满足条件的集合C是存在的.
5.命题p:“若x2<1,则x<1”的逆命题为q,则p与q的真假性为( )
A.p真q真 B.p真q假
C.p假q真 D.p假q假
解析:选B q:若x<1,则x2<1.
∵p:x2<1,则-10”是“S4+S6>2S5”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:选C 因为{an}为等差数列,所以S4+S6=4a1+6d+6a1+15d=10a1+21d,2S5=10a1+20d,S4+S6-2S5=d,所以d>0⇔S4+S6>2S5.
7.在△ABC中,“A=B”是“tan A=tan B”的________条件.
解析:由A=B,得tan A=tan B,反之,若tan A=tan B,则A=B+kπ,k∈Z.∵0<A<π,00,若p(1)是假命题,p(2)是真命题,则实数m的取值范围为________.
解析:因为p(1)是假命题,所以1+2-m≤0,解得m≥3.
又p(2)是真命题,所以4+4-m>0,解得m<8.
故实数m的取值范围是[3,8).
答案:[3,8)
9.下列命题:
①“a>b”是“a2>b2”的必要条件;
②“|a|>|b|”是“a2>b2”的充要条件;
③“a>b”是“a+c>b+c”的充要条件.
其中真命题的是________(填序号).
解析:①a>b⇒/ a2>b2,且a2>b2⇒/ a>b,故①不正确;
②a2>b2⇔|a|>|b|,故②正确;
③a>b⇒a+c>b+c,且a+c>b+c⇒a>b,故③正确.
答案:②③
10.(2018·德州模拟)下列命题中为真命题的序号是________.
①若x≠0,则x+≥2;
②命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1且x≠-1,则x2≠1;
③“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件;
④命题“若x<-1,则x2-2x-3>0”的否命题为“若x≥-1,则x2-2x-3≤0”.
解析:当x<0时,x+≤-2,故①错误;根据逆否命题的定义可知,②正确;“a=±1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件,故③错误;根据否命题的定义知④正确.故填②④.
答案:②④
B级——中档题目练通抓牢
1.(2018·河南开封二十五中月考)下列命题中为真命题的是( )
A.命题“若x>1,则x2>1”的否命题
B.命题“若x>y,则x>|y|”的逆命题
C.命题“若x=1,则x2+x-2=0”的否命题
D.命题“若>1,则x>1”的逆否命题
解析:选B 对于A,命题“若x>1,则x2>1”的否命题为“若x≤1,则x2≤1”,易知当x=-2时,x2=4>1,故为假命题;对于B,命题“若x>y,则x>|y|”的逆命题为“若x>|y|,则x>y”,分析可知为真命题;对于C,命题“若x=1,则x2+x-2=0”的否命题为“若x≠1,则x2+x-2≠0”,易知当x=-2时,x2+x-2=0,故为假命题;对于D,命题“若>1,则x>1”的逆否命题为“若x≤1,则≤1”,易知为假命题,故选B.
2.如果x,y是实数,那么“x≠y”是“cos x≠cos y”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
解析:选C 设集合A={(x,y)|x≠y},B={(x,y)|cos x≠cos y},则A的补集C={(x,y)|x=y},B的补集D={(x,y)|cos x=cos y},显然C?D,所以B?A.于是“x≠y”是“cos x≠cos y”的必要不充分条件.
3.若x>5是x>a的充分条件,则实数a的取值范围为( )
A.(5,+∞) B.[5,+∞)
C.(-∞,5) D.(-∞,5]
解析:选D 由x>5是x>a的充分条件知,{x|x>5}⊆{x|x>a},∴a≤5,故选D.
4.在命题“若m>-n,则m2>n2”的逆命题、否命题、逆否命题中,假命题的个数是________.
解析:若m=2,n=3,则2>-3,但22<32,所以原命题为假命题,则逆否命题也为假命题,若m=-3,n=-2,则(-3)2>(-2)2,但-3<2
,所以逆命题是假命题,则否命题也是假命题.故假命题的个数为3.
答案:3
5.(2018·武汉调研)已知“命题p:(x-m)2>3(x-m)”是“命题q:x2+3x-4<0”成立的必要不充分条件,则实数m的取值范围为________________.
解析:命题p:x>m+3或x<m,
命题q:-4<x<1.
因为p是q成立的必要不充分条件,
所以m+3≤-4或m≥1,
故m≤-7或m≥1.
答案:(-∞,-7]∪[1,+∞)
6.写出命题“已知a,b∈R,若关于x的不等式x2+ax+b≤0有非空解集,则a2≥4b”的逆命题、否命题、逆否命题,并判断它们的真假.
解:(1)逆命题:已知a,b∈R,若a2≥4b,则关于x的不等式x2+ax+b≤0有非空解集,为真命题.
(2)否命题:已知a,b∈R,若关于x的不等式x2+ax+b≤0没有非空解集,则a2<4b,为真命题.
(3)逆否命题:已知a,b∈R,若a2<4b,则关于x的不等式x2+ax+b≤0没有非空解集,为真命题.
7.已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若x∈A是x∈B的充分条件,求a的取值范围;
(2)若A∩B=∅,求a的取值范围.
解:A={x|x2-6x+8<0}={x|20时,B={x|a0时,B={x|a-3,但22<32,所以原命题为假命题,则逆否命题也为假命题,若m=-3,n=-2,则(-3)2>(-2)2,但-3<2,所以逆命题是假命题,则否命题也是假命题.故假命题的个数为3.
答案:3
7.有下列几个命题:
①“若a>b,则a2>b2”的否命题;
②“若集合A是集合B的子集,则集合A是集合B的真子集”的逆命题;
③“若x2<4,则-2<x<2”的逆否命题.
其中真命题的序号是________.
解析:①原命题的否命题为“若a≤b,则a2≤b2”,是假命题,如-1<0,但是(-1)2>0;②原命题的逆命题为“若集合A是集合B的真子集,则集合A是集合B的子集”是真命题;③原命题的逆否命题为“若x≥2或x≤-2,则x2≥4”,是真命题.
答案:②③
8.已知p(x):x2+2x-m>0,若p(1)是假命题,p(2)是真命题,则实数m的取值范围为________.
解析:因为p(1)是假命题,
所以1+2-m≤0,解得m≥3.
又p(2)是真命题,所以4+4-m>0,解得m<8.
故实数m的取值范围是[3,8).
答案:[3,8)
9.写出命题“已知a,b∈R,若关于x的不等式x2+ax+b≤0有非空解集,则a2≥4b”的逆命题、否命题、逆否命题,并判断它们的真假.
解:(1)逆命题:已知a,b∈R,若a2≥4b,则关于x的不等式x2+ax+b≤0有非空解集,为真命题.
(2)否命题:已知a,b∈R,若关于x的不等式x2+ax+b≤0没有非空解集,则a2<4b,为真命题.
(3)逆否命题:已知a,b∈R,若a2<4b,则关于x的不等式x2+ax+b≤0没有非空解集,为真命题.
10.(2018·安徽黄山调研)已知条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0.若綈p是綈q的必要不充分条件,求实数a的取值范围.
解:由2x2-3x+1≤0,得≤x≤1,
∴条件p对应的集合P=.
由x2-(2a+1)x+a(a+1)≤0,得a≤x≤a+1,
∴条件q对应的集合为Q={x|a≤x≤a+1}.
∵綈p是綈q的必要不充分条件,
∴根据原命题与逆否命题等价,得p是q的充分不必要条件.
∴p⇒q,即P?Q⇔或
解得0≤a≤.
∴实数a的取值范围为.
B级——拔高题目稳做准做
1.已知命题p:x2+2x-3>0;命题q:x>a,且綈q的一个充分不必要条件是綈p,则a的取值范围是( )
A.[1,+∞) B.(-∞,1]
C.[-1,+∞) D.(-∞,-3]
解析:选A 由x2+2x-3>0,得x<-3或x>1,由綈q的一个充分不必要条件是綈p,可知綈p是綈q的充分不必要条件,等价于q是p的充分不必要条件.故a≥1.
2.(2017·天津高考)设θ∈R,则“<”是“sin θ<”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:选A 法一:由<,得0<θ<,
故sin θ<.由sin θ<,得-+2kπ<θ<+2kπ,k∈Z,推不出“<”.
故“<”是“sin θ<”的充分而不必要条件.
法二:<⇒0<θ<⇒sin θ<,而当sin θ<时,取θ=-,=>.
故“<”是“sin θ<”的充分而不必要条件.
3.设等比数列{an}的公比为q,前n项和为Sn,则“|q|=1”是“S4=2S2”的________条件.
解析:∵等比数列{an}的前n项和为Sn,又S4=2S2,
∴a1+a2+a3+a4=2(a1+a2),
∴a3+a4=a1+a2,
∴q2=1⇔|q|=1,
∴“|q|=1”是“S4=2S2”的充要条件.
答案:充要
4.(2018·武汉调研)已知“命题p:(x-m)2>3(x-m)”是“命题q:x2+3x-4<0”成立的必要不充分条件,则实数m的取值范围为________________.
解析:命题p:x>m+3或x<m,
命题q:-4<x<1.
因为p是q成立的必要不充分条件,
所以m+3≤-4或m≥1,
故m≤-7或m≥1.
答案:(-∞,-7]∪[1,+∞)
5.已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=∅”是假命题,求实数m的取值范围.
解:因为“A∩B=∅”是假命题,所以A∩B≠∅.
设全集U={m|Δ=(-4m)2-4(2m+6)≥0},
则U=.
假设方程x2-4mx+2m+6=0的两根x1,x2均非负,则有即解得m≥.
又集合关于全集U的补集是{m|m≤-1},
所以实数m的取值范围是(-∞,-1].
6.已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若x∈A是x∈B的充分条件,求a的取值范围;
(2)若A∩B=∅,求a的取值范围.
解:已知A={x|x2-6x+8<0}={x|20时,B={x|a0时,B={x|a
查看更多