2019届二轮复习专题九　复　数课件（11张）（全国通用）

2019届二轮复习专题九　复　数课件（11张）（全国通用）

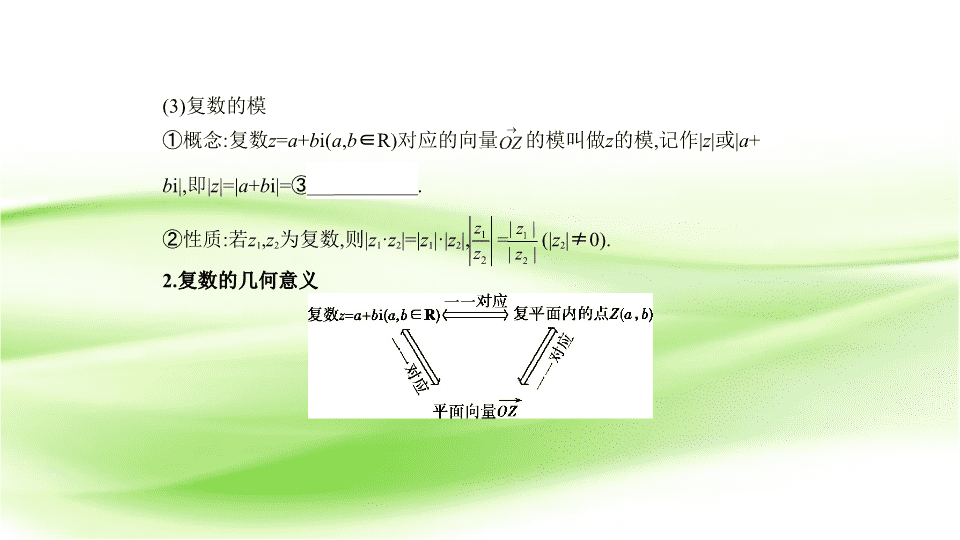
考点一    复数的有关概念及几何意义 考点清单 考向基础 1.复数的有关概念 (1)复数相等: a + b i= c + d i ⇔ ①      a = c 且 b = d      ( a , b , c , d ∈R). (2)共轭复数: a + b i与 c + d i共轭 ⇔ ②      a = c , b =- d      ( a , b , c , d ∈R). (3)复数的模 ①概念:复数 z = a + b i( a , b ∈R)对应的向量   的模叫做 z 的模,记作| z |或| a + b i|,即| z |=| a + b i|=③             . ②性质:若 z 1 , z 2 为复数,则| z 1 · z 2 |=| z 1 |·| z 2 |,   =   (| z 2 | ≠ 0). 2.复数的几何意义 考向突破 考向一    复数的有关概念 例1　 设复数 z 满足   =i(i为虚数单位),则| z |= 　　　     . 解析 　由题意知1+ z =i- z i,所以 z =   =   =i,所以| z |=1. 答案　 1 考向二    复数的几何意义 例2     (2019届江苏如东栟茶中学检测)设复数 z =   (i为虚数单位), z 的 共轭复数为   ,则在复平面内i   对应的点的坐标为 　　　     . 解析 　因为 z =   =-1+i,所以i   =i(-1-i)=1-i,其在复平面内对应的点的 坐标为(1,-1). 答案　 (1,-1) 考点二    复数的运算 考向基础 1.复数的加、减、乘、除运算法则 设 z 1 = a + b i, z 2 = c + d i( a , b , c , d ∈R),则 加法: z 1 + z 2 =( a + b i)+( c + d i)=( a + c )+( b + d )i; 减法: z 1 - z 2 =( a + b i)-( c + d i)=( a - c )+( b - d )i; 乘法: z 1 · z 2 =( a + b i)·( c + d i)=( ac - bd )+( bc + ad )i; 除法:   =   =   =   +   i( c + d i ≠ 0). 2.复数加法的运算律 复数的加法满足交换律、结合律,即对任意 z 1 、 z 2 、 z 3 ∈C,有 z 1 + z 2 = z 2 + z 1 , ( z 1 + z 2 )+ z 3 = z 1 +( z 2 + z 3 ). 3.i、 ω 常用的性质 (1)i 4 k =1,i 4 k +1 =i,i 4 k +2 =-1,i 4 k +3 =-i,其中 k ∈N * . (2)(1 ± i) 2 = ± 2i;   =i;   =-i; i n +i n +1 +i n +2 +i n +3 =0( n ∈N * ). (3) ω =-   +   i,则 ω 3 =1, ω n + ω n +1 + ω n +2 =0( n ∈N * ). 4.共轭复数及其运算性质 z = a + b i( a , b ∈R)与   = a - b i互为共轭复数 ,且 z +   =2 a , z -   =2 b i, z ·   =| z | 2 =|   | 2 ,它 的运算性质有   =   ±   ,   =   ·   ,   =   ( z 2 ≠ 0). 5.复数模的性质 (1)|| z 1 |-| z 2 || ≤ | z 1 ± z 2 | ≤ | z 1 |+| z 2 |; (2)| z | 2 = z ·   ; (3)| z |=1 ⇔ z ·   =1; (4)| z | 2 =|   | 2 =| z 2 |=|   |= z ·   . 考向突破 考向    复数的四则运算 例　 (1)(2019届江苏邗江中学检测)设i是虚数单位,则复数i 3 -   = 　　         . (2)(2019届江苏启东中学检测)若复数 z =1+2i,其中i是虚数单位,则   ·   = 　　　     . 解析 　(1)i 3 -   =-i-   =-i+2i=i. (2)因为 z =1+2i, 所以   =1-2i, 所以   ·   = z ·   +1=5+1=6. 答案 　(1)i　(2)6 方法一    复数四则运算的方法 1. 巧用“分母实数化”求解复数除法运算. 复数的除法一般是将分母实数化,即分子、分母同乘分母的共轭复数, 再进一步化简.其原理是( a + b i)( a - b i)= a 2 + b 2 ( a 、 b ∈R). 2. 巧用“结论”求解复数的乘方运算. 在进行复数的代数运算时,记住以下结论,可提高计算速度. (1)(1 ± i) 2 = ± 2i;   =i;   =-i; (2)- b + a i=i( a + b i); (3)i 4 n =1,i 4 n +1 =i,i 4 n +2 =-1,i 4 n +3 =-i,i 4 n +i 4 n +1 +i 4 n +2 +i 4 n +3 =0, n ∈N * . 方法技巧 例1 　计算:(1)   ; (2)   +   . 解析 　(1)   =   =-1-3i. (2)   +   =   +   =   +   =-1. 方法二    复数几何意义有关问题的应用方法 1. 复数 z 、复平面上的点 Z 及向量   相互联系,即 z = a + b i( a , b ∈R) ⇔ Z ( a , b ) ⇔   . 2. 由于复数、复平面上的点、向量之间建立了一一对应的关系,因此可 把复数、向量与解析几何联系在一起,解题时可运用数形结合思想. 例2     (2019届江苏海安中学检测)△ ABC 的三个顶点对应的复数分别为 z 1 , z 2 , z 3 ,若复数 z 满足| z - z 1 |=| z - z 2 |=| z - z 3 |,则 z 对应的点为△ ABC 的 　　　     . 解析 　由几何意义知,复数 z 对应的点到△ ABC 三个顶点的距离都相等, 则 z 对应的点是△ ABC 的外心. 答案 　外心