2019年相阳教育“黉门云”高考等值试卷★预测卷（全国I卷）数学（理）

2019年相阳教育“黉门云”高考等值试卷★预测卷（全国I卷）数学（理）

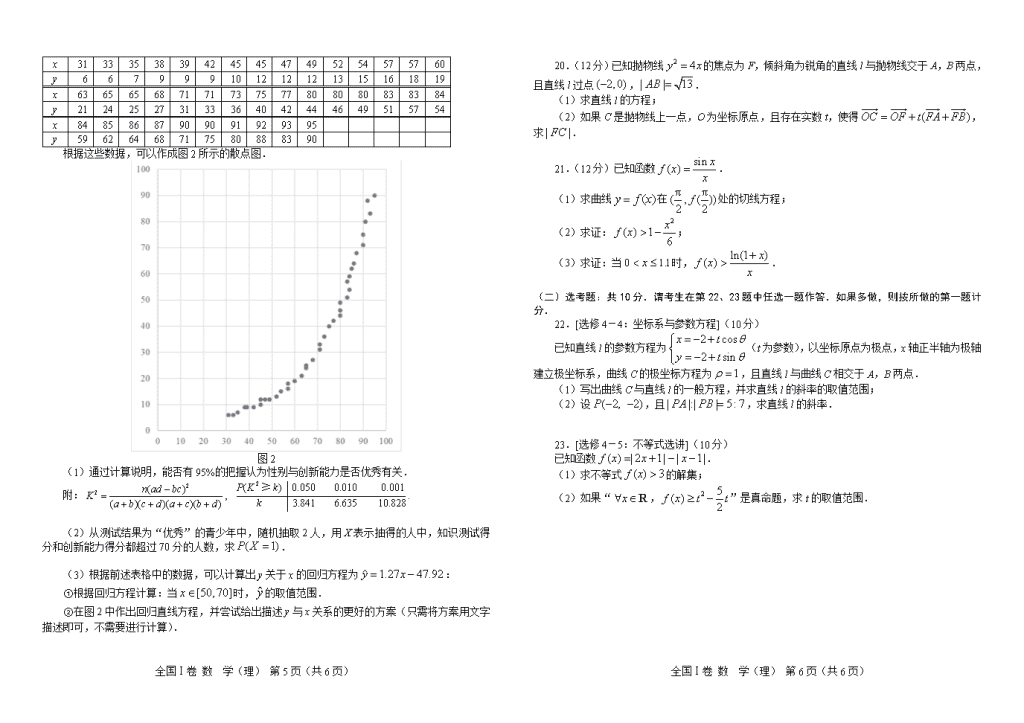
‎2019年相阳教育“黉门云”高考等值试卷★预测卷 理科数学（全国I卷）‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。全卷满分150分，考试用时120分钟。‎ 注意事项：‎ ‎ 1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。 ‎ ‎2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，在选涂其他答案标号。第Ⅱ卷必须用0.5毫米黑色签字笔书写作答.若在试题卷上作答，答案无效。‎ ‎ 3.考试结束，请将试题卷、答题卡一并收回。‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知i为虚数单位，则 ‎（A） （B） （C） （D）‎ ‎2．已知集合，，且，则实数a的取值范围是 ‎（A） （B） （C） （D）‎ ‎3．已知数列的首项为1，且对于所有大于1的正整数n都成立，，则 ‎（A）34 ‎ ‎（B）17 ‎ ‎（C）36‎ ‎（D）18 ‎ ‎4．有关数据表明，2018年我国固定资产投资（不含农户，下同）635636亿元，增长5.9%．其中，第一产业投资22413亿元，比上年增长12.9%；第二产业投资237899亿元，增长6.2%；第三产业投资375324亿元，增长5.5%．另外，2014—2018年，我国第一产业、第二产业、第三产业投资占固定资产投资比重情况如下图所示．‎ 根据以上信息可知，下列说法中： ‎ ‎①2014—2018年，我国第一产业投资占固定资产投资比重逐年增加；‎ ‎②2014—2018年，我国第一产业、第三产业投资之和占固定资产投资比重逐年增加；‎ ‎③；‎ ‎④．‎ 不正确的个数为 ‎（A）1 （B）2 （C）3 （D）4‎ ‎5．已知，，则下列说法中，正确的是 ‎（A）， （B），‎ ‎（C）， （D），‎ ‎6．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为 ‎（A） （B）‎ ‎（C） （D）‎ ‎7．已知点P为△ABC所在平面内一点，且，如果E为AC的中点，F为BC的中点，则下列结论中：‎ ‎①向量与可能平行；‎ ‎②向量与可能垂直；‎ ‎③点P在线段EF上；‎ ‎④．‎ 正确的个数为 ‎（A）1 ‎ ‎（B）2‎ ‎（C）3‎ ‎（D）4‎ ‎8．已知椭圆（）经过点，过顶点，的直线与圆相切，则椭圆的方程为 ‎（A） （B） （C） （D）‎ ‎9．已知某品牌的手机从1米高的地方掉落时，第一次未损坏的概率为0.3，在第一次未损坏的情况下第二次也未损坏的概率为0.1．则这样的手机从1米高的地方掉落两次后仍未损坏的概率为 ‎（A）0.25 （B）0.15 （C）0.1 （D）0.03‎ 全国Ⅰ卷 数 学（理） 第5页（共6页） 全国Ⅰ卷 数 学（理） 第6页（共6页）‎ ‎10．如果在区间内有且只有一个实数解，则实数a的取值范围是 ‎（A） （B）或 ‎（C） （D）或 ‎11．《九章算术》是中国古典数学最重要的著作．《九章算术》的“商功”一章中给出了很多几何体的体积计算公式．如图所示的几何体，上底面与下底面相互平行，且与均为长方形．《九章算术》中，称如图所示的图形为“刍童”．如果，，，，且两底面之间的距离为h，记“刍童”的体积为V，则 ‎（A） （B）‎ ‎（C） （D）‎ ‎12．已知数列的前项的和为，且，，．又已知当时，恒成立．则使得 成立的正整数的取值集合为 ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．在了解全校学生每年平均阅读了多少本文学经典名著时，甲同学抽取了一个容量为10的样本，并算得样本的平均数为6；乙同学抽取了一个容量为15的样本，并算得样本的平均数为5．已知甲、乙两同学抽取的样本合在一起正好组成一个容量为25的样本，则合在一起后的样本的平均数为_____________．‎ ‎14．已知是第四象限角，且，则_____________．‎ ‎15. 在平面直角坐标系中，过点的一条直线与函数的图像交于，两点，则线段长的最小值是 ．‎ ‎16．双曲线的左、右焦点分别为，，左、右顶点分别为，，P为双曲线上一点，已知直线，的斜率之积为，，到一条渐近线的距离为，则：‎ ‎（1）双曲线的方程为_______________；‎ ‎（2）△的内切圆半径与外接圆半径之比为_______________．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17题～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答．‎ ‎（一）必考题：共60分．‎ ‎17．（12分）‎ 已知△ABC中，为钝角，而且，，AB边上的高为．‎ ‎（1）求的大小；‎ ‎（2）求的值．‎ ‎18．（12分）如图，AB，CD分别是圆柱下底面、上底面的直径，AD，BC分别是圆柱的母线，ABCD是一个边长为2的正方形，E，F都是下底面圆周上的点，且，，点P在上底面圆周上运动．‎ ‎（1）判断直线AF是否有可能与平面PBE平行，并说明理由；‎ ‎（2）判断直线BE是否有可能与平面PAE垂直，并说明理由；‎ ‎（3）设平面PAE与平面ABCD所成夹角为（），求的取值范围．‎ ‎19．（12分）为了了解青少年的创新能力与性别的联系，某研究院随机抽取了若干名青少年进行测试，所得结果如图1所示．‎ 图1‎ 更进一步，该研究院对上述测试结果为“优秀”的青少年进行了知识测试，得到了每个人的知识测试得分x和创新能力得分y，所得数据如下表所示．‎ 全国Ⅰ卷 数 学（理） 第5页（共6页） 全国Ⅰ卷 数 学（理） 第6页（共6页）‎ x ‎31‎ ‎33‎ ‎35‎ ‎38‎ ‎39‎ ‎42‎ ‎45‎ ‎45‎ ‎47‎ ‎49‎ ‎52‎ ‎54‎ ‎57‎ ‎57‎ ‎60‎ y ‎6‎ ‎6‎ ‎7‎ ‎9‎ ‎9‎ ‎9‎ ‎10‎ ‎12‎ ‎12‎ ‎12‎ ‎13‎ ‎15‎ ‎16‎ ‎18‎ ‎19‎ x ‎63‎ ‎65‎ ‎65‎ ‎68‎ ‎71‎ ‎71‎ ‎73‎ ‎75‎ ‎77‎ ‎80‎ ‎80‎ ‎80‎ ‎83‎ ‎83‎ ‎84‎ y ‎21‎ ‎24‎ ‎25‎ ‎27‎ ‎31‎ ‎33‎ ‎36‎ ‎40‎ ‎42‎ ‎44‎ ‎46‎ ‎49‎ ‎51‎ ‎57‎ ‎54‎ x ‎84‎ ‎85‎ ‎86‎ ‎87‎ ‎90‎ ‎90‎ ‎91‎ ‎92‎ ‎93‎ ‎95‎ y ‎59‎ ‎62‎ ‎64‎ ‎68‎ ‎71‎ ‎75‎ ‎80‎ ‎88‎ ‎83‎ ‎90‎ 根据这些数据，可以作成图2所示的散点图．‎ 图2‎ ‎（1）通过计算说明，能否有95%的把握认为性别与创新能力是否优秀有关．‎ 附： ‎ ‎（2）从测试结果为“优秀”的青少年中，随机抽取2人，用X表示抽得的人中，知识测试得分和创新能力得分都超过70分的人数，求．‎ ‎（3）根据前述表格中的数据，可以计算出y关于x的回归方程为：‎ ‎①根据回归方程计算：当时，的取值范围．‎ ‎②在图2中作出回归直线方程，并尝试给出描述y与x关系的更好的方案（只需将方案用文字描述即可，不需要进行计算）．‎ ‎20．（12分）已知抛物线的焦点为F，倾斜角为锐角的直线l与抛物线交于A，B两点，且直线l过点，．‎ ‎（1）求直线l的方程；‎ ‎（2）如果C是抛物线上一点，O为坐标原点，且存在实数t，使得，求．‎ ‎21．（12分）已知函数．‎ ‎（1）求曲线在处的切线方程；‎ ‎（2）求证：；‎ ‎（3）求证：当时，．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．‎ ‎22．[选修4－4：坐标系与参数方程]（10分）‎ 已知直线l的参数方程为（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为，且直线l与曲线C相交于A，B两点．‎ ‎（1）写出曲线C与直线l的一般方程，并求直线l的斜率的取值范围；‎ ‎（2）设，且，求直线l的斜率． ‎ ‎23．[选修4－5：不等式选讲]（10分）‎ 已知函数．‎ ‎（1）求不等式的解集；‎ ‎（2）如果“，”是真命题，求t的取值范围．‎ 全国Ⅰ卷 数 学（理） 第5页（共6页） 全国Ⅰ卷 数 学（理） 第6页（共6页）‎