2020届高考文科数学模拟黄金卷（全国卷）（一）

2020届高考文科数学模拟黄金卷（全国卷）（一）

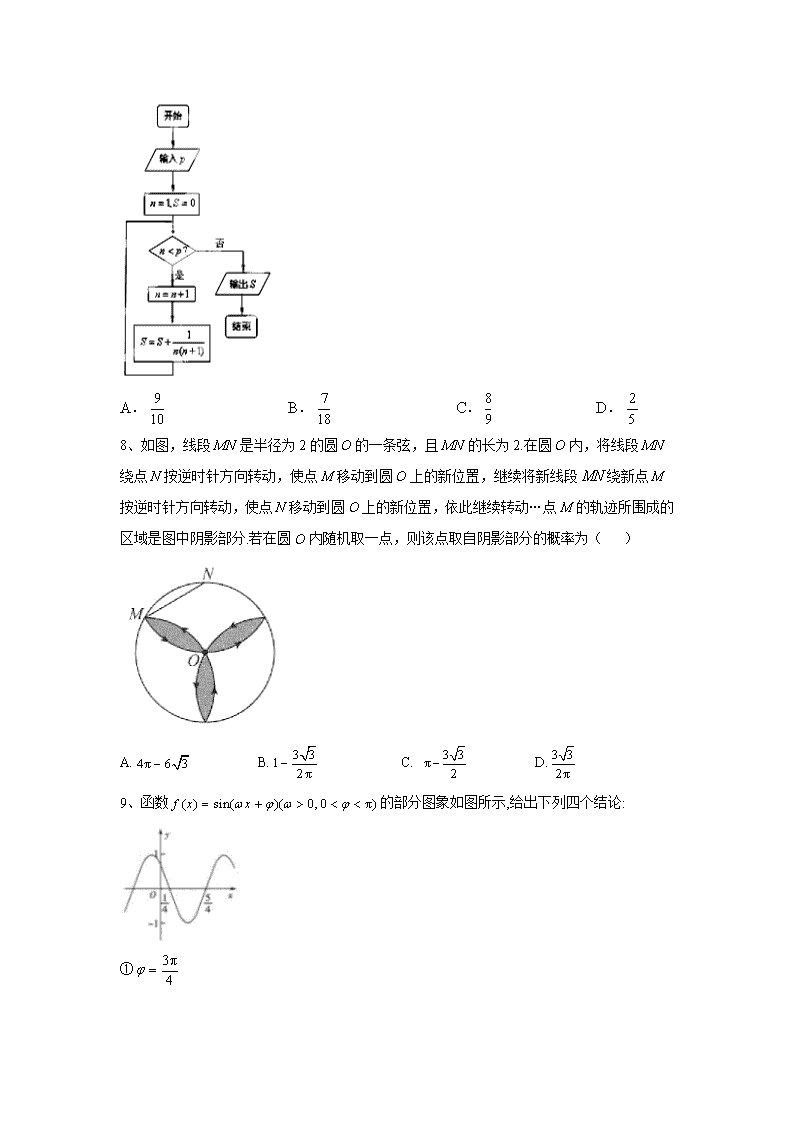
‎2020届高考文科数学模拟黄金卷（全国卷）（一）‎ ‎1、已知集合，则=（ ）‎ A． B． C． D．‎ ‎2、已知，i为虚数单位，且，则( )‎ A. B. C.2 D. ‎ ‎3、已知是过抛物线焦点F的直线与抛物线的交点，O是坐标原点，且满足,,则抛物线的标准方程为（ ）‎ A． B． C． D．‎ ‎4、设向量,,若向量与同向,则(   )‎ A.2 B.-2 C. D. 0‎ ‎5、已知函数，则函数的图像只可能是( )‎ ‎6、若满足约束条件,则的最大值为( )‎ A.-6, B.-2 C.2 D.4‎ ‎7、执行如图的程序框图,若,则输出的S= （ ）‎ A． B． C． D．‎ ‎8、如图，线段是半径为2的圆O的一条弦，且的长为2.在圆O内，将线段绕点N按逆时针方向转动，使点M移动到圆O上的新位置，继续将新线段绕新点M按逆时针方向转动，使点N移动到圆O上的新位置，依此继续转动…点M的轨迹所围成的区域是图中阴影部分.若在圆O内随机取一点，则该点取自阴影部分的概率为（ ）‎ ‎ A. B. C. D.‎ ‎9、函数的部分图象如图所示,给出下列四个结论:‎ ‎①‎ ‎②‎ ‎③当时,的最小值为-1‎ ‎④在上单调递增 其中所有正确结论的序号是( )‎ A.①②④ B.②③ C.①② D. ①②③④‎ ‎10、若关于x的方程没有实数根，则实数a的取值范围是（ ）‎ A． B． C． D．‎ ‎11、在中，若，则的面积为（ ）‎ A.8 B.2 C. D.4‎ ‎12、已知双曲线的焦点为,渐近线为,过点且与平行的直线交于M,若,则m的值为( )‎ A.1 B. C.2 D.3‎ ‎13、某单位有840名职工，现采用系统抽样方法抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间的人数为________.‎ ‎14、已知函数把函数的图象与直线交点的横坐标按从小到大的顺序排成一个数列则数列的前n项和________.‎ ‎15、已知直线为曲线的一条切线，则实数a的值为 .‎ ‎16、在正方体中，E为棱的中点，则异面直线AE与CD所成角的正切值为______________.‎ ‎17、已知各项都不相等的等差数列,,又成等比数列.‎ ‎1.求数列的通项公式 ‎2.设,求数列的前n项和为.‎ ‎18、如图，在四棱锥中，平面平面, , , ， ,M是 的中点．‎ ‎(1)求证：平面；‎ ‎(2)求三棱锥的体积．‎ ‎19、为喜迎元旦,某电子产品店规定的买超过5 000元电子产品的顾客可以今与抽奖活动，中奖者可获得扫地机器人一台.现有甲品牌和乙品牌的扫地机器人作为奖品.从这两种品牌的扫地机器人中各随机抽取6台,检侧它们充满电后的工作时长(单位:分).相关数据如下表所示.‎ 机器序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 甲品牌扫地机器人工作时长/分 ‎220‎ ‎180‎ ‎210‎ ‎220‎ ‎200‎ ‎230‎ 乙品牌扫地机器人工作时长/分 ‎200‎ ‎190‎ ‎240‎ ‎230‎ ‎220‎ ‎210‎ ‎(1)根据所提供的数据分别计算抽取的甲、乙两种品牌扫地机器人充润电后工作时长的平均数与方差.‎ ‎(2)从甲品牌被抽中的6台扫地机器人中随机抽出2台.求抽出的2台扫地机器人充满电后工作时长之和小于420分钟的概率 ‎(3)下表是一台乙品牌扫地机器人的使用次效与当次充满电后工作时长的相关欲据.求该扫地机器人工作时长y与使用次数x之间的回归直线方程，并估计该扫地机舒人使用第200次时间充满电后的工作时长 使用次数x ‎20‎ ‎40‎ ‎60‎ ‎80‎ ‎100‎ ‎120‎ ‎140‎ 工作时长y/分 ‎210‎ ‎206‎ ‎202‎ ‎196‎ ‎191‎ ‎188‎ ‎186‎ 附,,‎ ‎20、已知椭圆的四个顶点围成的菱形的面积为，椭圆的一个焦点为圆的圆心 ‎(1)求椭圆的方程.‎ ‎(2)若为椭圆上的两个动点，直线的斜率分别为，当时，的面积是否为定值？若为定值，求出此定值；若不为定值，请说明理由 ‎21、设.‎ ‎(1)若对一切恒成立,求a的最大值;‎ ‎(2)是否存在正整数a,使得对一切正整数n都成立？若存在,求a的最小值;若不存在,请说明理由.‎ ‎22、在直角坐标系中,以为极点, 轴正半轴为极轴建立极坐标系,直线的参数方程为 (为参数),曲线的方程为,定点,点是曲线上的动点, 为的中点. （1）求点的轨迹的直角坐标方程; （2）直线与直线交于两点,若,求实数的取值范围.‎ ‎23、设函数，．‎ ‎(1)当时，求不等式的解集.‎ ‎(2)对任意，恒有，求实数a的取值范围．‎ ‎ ‎ ‎ ‎ ‎ ‎ 答案以及解析 ‎1答案及解析：‎ 答案：C 解析：∵，，‎ ‎∴‎ ‎ ‎ ‎2答案及解析：‎ 答案：B 解析：∵,i为虚数单位,且,∴，解得.‎ 则.‎ 故选：B.‎ ‎ ‎ ‎3答案及解析：‎ 答案：A 解析：设, ，则，又由抛物线焦点弦性质， ，所以，得， ，‎ 得。 ，‎ 得 ，抛物线的标准方程为，故选A ‎ ‎ ‎4答案及解析：‎ 答案：A 解析：由题意得且,所以,故选A.‎ ‎ ‎ ‎5答案及解析：‎ 答案：C 解析：函数是偶函数, 是偶函数，‎ 故排除A. D，‎ 当时, ，‎ 故选C.‎ ‎ ‎ ‎6答案及解析：‎ 答案：D 解析：作出可行域如图阴影部分所示,由图可知当直线经过点时,z取得最大值,选D ‎ ‎ ‎7答案及解析：‎ 答案：D 解析：根据题意，本程序框图为求和运算，程序执行如下：‎ 第1次循环：‎ 第2次循环：‎ ‎…‎ 第8次循环：‎ 此时，，输出 ‎ ‎ ‎8答案及解析：‎ 答案：B 解析：圆O的面积为，阴影部分的面积为，则所求概率为.‎ ‎ ‎ ‎9答案及解析：‎ 答案：C 解析：由题图得,得,所以①正确 ‎,所以②正确 当时,,所以的最小值是,所以③不正确;令,解得,所以的单调递增区间为,当时,的单调递增区间为,所以④不正确,故选C ‎ ‎ ‎10答案及解析：‎ 答案：A 解析：‎ 方程没有实数根，得方程没有实数根，‎ 等价为函数与没有交点，‎ 当时，直线与恒有交点，不满足条件．‎ 当时，直线与没有交点，满足条件．‎ 当时，当过点的直线相切时，设切点为，则，则，‎ 则切线方程为．即，‎ ‎∵切线过点，则，得，即切线斜率为，‎ 要使与没有交点，则满足，即，‎ 综上，即实数a的取值范围是．‎ ‎ ‎ ‎11答案及解析：‎ 答案：C 解析：中，，则，‎ 又，‎ ‎∴，‎ ‎，，‎ ‎∴，‎ 的面积为.‎ ‎ ‎ ‎12答案及解析：‎ 答案：D 解析：不妨设,所以过点且与渐近线平行的直线方程为,由,解得,所以,所以,‎ ‎.因为,所以,即,解得或(舍去).故选D.‎ ‎ ‎ ‎13答案及解析：‎ 答案：12‎ 解析：采用系统抽样的方法,从840人中抽取42人,则分段间隔为20,所以从编号落在区间内的240人中抽取12(人).‎ ‎ ‎ ‎14答案及解析：‎ 答案：‎ 解析：当时;‎ 当时, ‎ 当时,‎ 当时,‎ 当时,易知 所以令又有唯一解 所以,故,所以 ‎ ‎ ‎ ‎ ‎15答案及解析：‎ 答案：‎ 解析：设曲线在点处的切线为直线.‎ 由题意，得，，‎ 则曲线在点处的切线方程为.‎ 曲线在点处的切线为直线，，‎ ‎，即，，解得.‎ ‎，解得.‎ ‎ ‎ ‎16答案及解析：‎ 答案：‎ 解析：如图，连接BE:‎ 因为，所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角，即 .不妨设正方体的棱长为2，则，由勾股定理得．又由平面BCC1B1可得，所以 ‎ ‎ ‎17答案及解析：‎ 答案：1.因为成等比数列,所以, ‎ 设公差为d,则,解得,‎ 又因为各项都不相等,所以,‎ 所以,‎ 由,所以. 2.由1知, ,所以数列的前n项和为 解析：‎ ‎ ‎ ‎18答案及解析：‎ 答案：(1)取中点N连接,‎ ‎∵为的中位线,∴,且，‎ 又∵且,∴，且，‎ 则为平行四边形,∴，‎ 又∵平面，平面，‎ ‎∴平面 .‎ ‎(2)过M作的垂线,垂足为，取中点，连结，‎ 又∵平面平面,平面平面平面，‎ ‎∴平面.‎ ‎∴为三棱锥的高，‎ ‎∵，为 中点，∴ ，‎ ‎∵，∴ 为等腰直角三角形，，‎ ‎∵平面平面 ,平面平面平面，‎ ‎∴ 平面.∴，‎ ‎∵M为的中点,∴，‎ 过C作，交于点H，‎ ‎∴,∵，∴为平行四边形，‎ ‎∴，‎ ‎，‎ ‎∴三棱锥的体积为：‎ ‎，‎ 解析： ‎ ‎ ‎ ‎19答案及解析：‎ 答案：(1)(分)‎ ‎(分)‎ ‎(2)记甲品牌中序号为n的扫地机器人为,则从这6‎ 台扫地机器人中随机抽取2台的所有情况为,共15种 其中满足条件的有共6种 记事件C为”抽出的2台扫地机器人充满电后工作时长之和不小于420分钟”‎ 则 ‎(3)计算的,‎ 所以 所以线性回归方程为 所以估计该扫地机器人使用第200次时冲满电后的工作时长为171.5分钟 解析： ‎ ‎ ‎ ‎20答案及解析：‎ 答案：(1)由题意可知，，‎ 圆的圆心坐标为，所以，‎ 因此，结合得，，‎ 故椭圆的方程为.‎ ‎(2)当直线的斜率存在时，设其方程为，，，‎ 由消去y可得，，‎ ‎，即，‎ ‎，.‎ 所以 ‎.‎ 又点O到直线的距离，‎ 所以，‎ 又 所以，‎ 化简可得，满足.‎ 则，‎ 当直线的斜率不存在时，由于，且关于x轴对称，‎ 不妨设，则易得，或，，‎ 此时.‎ 综上，的面积为定值，定值为.‎ 解析： ‎ ‎ ‎ ‎21答案及解析：‎ 答案：(1)∵,‎ ‎∴‎ 令,解得,令,‎ 则,令,则,‎ ‎∴,‎ ‎∵对一切恒成立,‎ ‎∴,‎ ‎∴,∴‎ ‎∴a的最大值为1.‎ ‎(2)设,‎ 则,令,得.‎ 当时,单调递减;当时,单调递增,‎ ‎∴的最小值为,故.‎ 取,‎ 得,即,‎ 累加得.‎ ‎∴.‎ 故存在正整数,使得.‎ 假设当时也符合题意,取,有,矛盾.‎ 故a的最小值为2.‎ 解析：‎ ‎ ‎ ‎22答案及解析：‎ 答案：（1）根据题意,得曲线的直角坐标方程为, 设点 ,‎ ‎,根据中点坐标公式, 得代入, 得点的轨迹的直角坐标方程为. （2）直线的直角坐标方程为, 根据题意,得圆心到直线的距离, 即,解得. ∴实数的取值范围为.‎ 解析：‎ ‎ ‎ ‎23答案及解析：‎ 答案：（1）当时，，‎ 的解集为．‎ ‎(2) ，‎ 又有，‎ 由题意恒成立得，，‎ 解得，∴a的取值范围为．‎ 解析： ‎ ‎ ‎