陕西省渭南市韩城市司马迁中学2020届高三第五次周考数学（理）试卷

陕西省渭南市韩城市司马迁中学2020届高三第五次周考数学（理）试卷

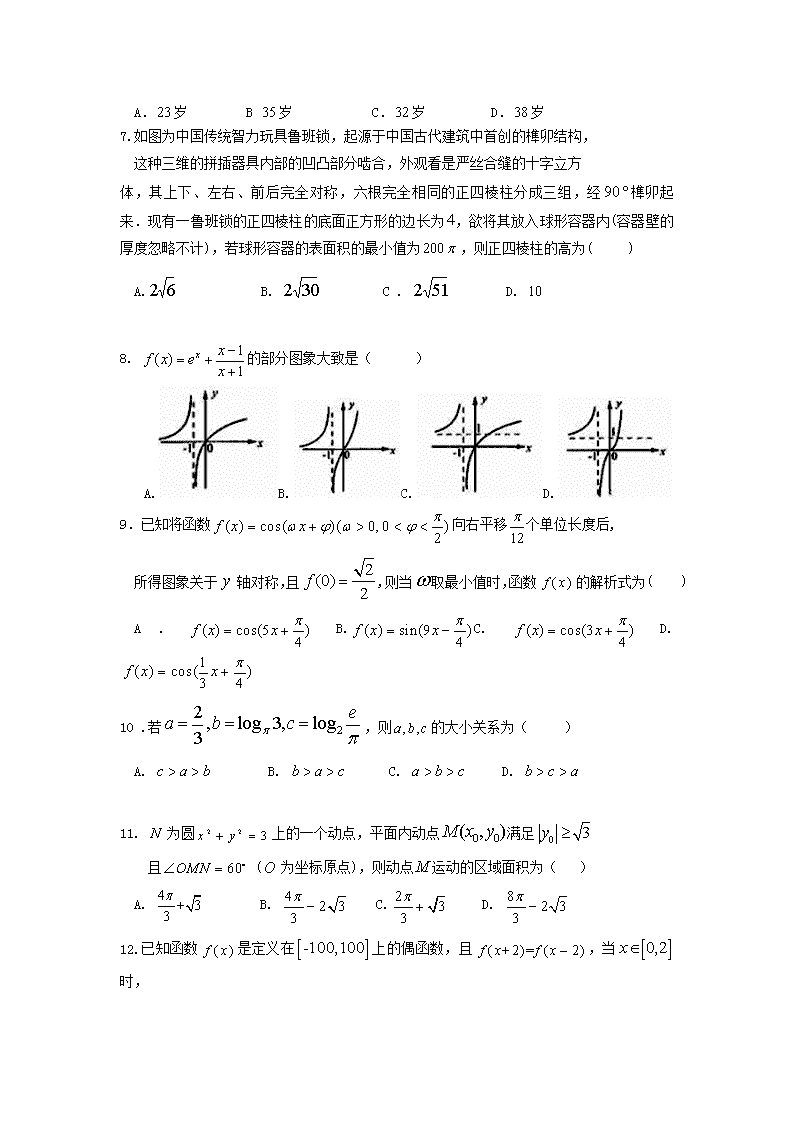
陕西省渭南市韩城市司马迁中学2020届高三第五次周考数学(理)试卷 一、选择题（每题5分，共60分）‎ ‎1.已知两个集合，，则（ ）‎ A. B. C. D. ‎ ‎2. 已知，若复数为纯虚数，则（ ）‎ ‎ A. B. C. D. ‎ ‎3 .已知直线、，平面、,给出下列命题:‎ ‎①若，且，则 ②若，且，则 ‎③若，且，则 ④若，且，则 其中正确的命题是( )‎ ‎ A.①③ B.②④ C.③④ D .①‎ ‎4.如果实数满足条件，则的最大值为（ ）‎ A． B． C． D． ‎ ‎5.已知双曲线的焦点到渐近线的距离为，且离心率为，则该双曲线的实轴的长为(　　)‎ A． B． C． D．‎ ‎6.《算法统宗》是中国古代数学名著，由明代数学家程大位编著，它对我国民间普及珠算和数学知识起到了很大的作用，是东方古代数学的名著．在这部著作中，许多数学问题都是以歌诀形式呈现的，如“九儿问甲歌”就是其中一首：一个公公九个儿，若问生年总不知，自长排来差三岁，共年二百又零七，借问长儿多少岁，各儿岁数要详推．在这个问题中，这位公公的长儿的年龄为（ ）‎ A． 岁 B 岁 C．岁 D．岁 ‎7.如图为中国传统智力玩具鲁班锁，起源于中国古代建筑中首创的榫卯结构，‎ 这种三维的拼插器具内部的凹凸部分啮合，外观看是严丝合缝的十字立方 体，其上下、左右、前后完全对称，六根完全相同的正四棱柱分成三组，经榫卯起来．现有一鲁班锁的正四棱柱的底面正方形的边长为，欲将其放入球形容器内(容器壁的厚度忽略不计)，若球形容器的表面积的最小值为，则正四棱柱的高为( 　) ‎ A. B. C . D. ‎ ‎8. 的部分图象大致是（  ）‎ A.B.C.D.‎ ‎9．已知将函数向右平移个单位长度后,‎ 所得图象关于轴对称，且,则当取最小值时，函数的解析式为( ) ‎ A． B.C. D.‎ ‎10 .若，则的大小关系为（ ）‎ ‎ A. B. C. D. ‎ 11. 为圆上的一个动点，平面内动点满足 且 (为坐标原点)，则动点运动的区域面积为（ ）‎ A. B. C. D. ‎ ‎12.已知函数是定义在上的偶函数，且，当时，‎ ‎，若方程 有个不同的实数根，‎ 则实数的取值范围为（ ）‎ A. ‎ B. ‎ ‎ C. D. ‎ 二、填空题（每题5分，共20分）‎ ‎13.公元前世纪，古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图，发现了黄金分割值约为，这一数值也可以表示为，若，则_________．‎ ‎14.若直线把圆分成面积相等的两部分，‎ 则取得最小值时,的值为_________．‎ 15. 已知向量满足，，‎ 则的夹角余弦值等于_______．‎ 16. 已知椭圆的左、右焦点分别为，，椭圆外一点 满足，且，线段，分别交椭圆于点，；若，‎ 则________________．‎ 三、解答题（共70分）‎ 17. ‎（分）‎ 已知数列和，前项和为，且,是各项均为正数的 等比数列，且，．‎ ‎（1）求数列和的通项公式；‎ ‎（2）求数列的前n项和．‎ 17. ‎（分）‎ 在直三棱柱ABCA1B1C1中，△ABC为正三角形，点D在棱BC上，且CD＝3BD，点E，F分别为棱AB，BB1的中点．‎ ‎(1)证明：A1C∥平面DEF；‎ ‎(2)若A1C⊥EF，求直线A1C1与平面DEF所成的角的正弦值．‎ ‎19 .（分）‎ 在中，.‎ ‎（1）求和C；‎ ‎（2）若，D是BC边上一点，且△ABD的面积为，求sin∠ADC.‎ ‎20.（分）‎ 已知椭圆的左、右焦点分别为，‎ 椭圆的离心率为，且椭圆过点．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若直线过椭圆的左顶点，且与椭圆的另一个交点为，直线与椭圆的另一个交点为，若，求直线的方程．‎ ‎21.（分）‎ 已知在处的切线是轴 ‎（1）求的单调区间；‎ ‎（2）若时，恒成立，求实数的取值范围.‎ ‎22.（分）[选修4—4：坐标系与参数方程]‎ 在平面直角坐标系中，曲线的参数方程为 (为参数)，将曲线上每一 点的横坐标变为原来的倍，纵坐标不变，得到曲线，以坐标原点为极点，轴的正半 轴为极轴建立极坐标系，射线与曲线交于点，将射线绕极点逆时针方向旋转 交曲线于点.‎ ‎（1）求曲线的参数方程；‎ ‎（2）求面积的最大值．‎ ‎. (分)[选修4－5：不等式选讲]‎ 已知函数 ‎（1）当时，求不等式的解集；‎ ‎（2）若且函数的最小值为，求的值．‎ ‎-6. BCDACB 7---12. BDCBBA 13. 14. 15. 16.‎ 17. ‎（1） （2）‎ 18. ‎ （1）略 （2） 19.（1）（2）‎ 19. ‎（1） （2）‎ ‎20.（1） （2）‎ ‎22.（1） （2）‎ ‎23（1）. （2）3‎