2020年高中数学第二章对数函数的图象及性质
2.2.2第1课时 对数函数的图象及性质
[课时作业]
[A组 基础巩固]
1.已知函数f(x)=的定义域为M,g(x)=ln(1+x)的定义域为N,则M∩N等于( )
A.{x|x>-1} B.{x|x<1}
C.{x|-1
-1},
则M∩N={x|-1<x<1}.
答案:C
2.函数y=2+log2x(x≥1)的值域为( )
A.(2,+∞) B.(-∞,2)
C.[2,+∞) D.[3,+∞)
解析:∵y=log2x在[1,+∞)是增函数,∴当x≥1时,log2x≥log21=0,
∴y=2+log2x≥2.
答案:C
3.与函数y=x的图象关于直线y=x对称的函数是( )
A.y=4x B.y=4-x
C.y=logx D.y=log4x
解析:y=ax与y=logax互为反函数,图象关于y=x对称.
答案:C
4.若函数f(x)=ax+loga(x+1)在[0,1]上的最大值和最小值之和为a,则函数g(x)=ax2+x+1在 [-2,2]上的值域为( )
A.[,5] B.[-,5]
C.[-,3] D.[0,3]
解析:显然函数f(x)=ax+loga(x+1)在[0,1]上是单调的,∴函数f(x)在[0,1]上的最大值和最小值之和为f(0)+f(1)=1+a+loga2=a,解得a=.
∴g(x)=x2+x+1在[-2,-1]上单调递减,在[-1,2]上单调递增.
∴g(x)=x2+x+1在[-2,2]上的值域为.故选A.
答案:A
4
5.函数f(x)=1+log2x与g(x)=21-x在同一直角坐标系下的图象大致是( )
解析:由对数函数y=log2x过定点(1,0)可知,函数f(x)=1+log2x的图象过定点(1,1),且是单调递增的.同理,函数g(x)=21-x的图象过定点(1,1),并且是单调递减的.观察函数图象可得选项C满足条件.
答案:C
6.设f(x)=则f(f(-2))=________.
解析:因为f(-2)=10-2>0,f(10-2)=lg 10-2=-2lg 10=-2,所以f(f(-2))=-2.
答案:-2
7.对数函数f(x)的图象过点(3,-2),则f()=________.
解析:设f(x)=logax,则loga3=-2,∴a-2=3,
∴a=,∴f(x)=,
∴f()==-1.
答案:-1
8.已知函数y=loga的图象恒过点P,则点P坐标为________.
解析:当=1时,x=-2,所以恒过点(-2,0).
答案:(-2,0)
9.(1)求函数y=log(x+1)(16-4x)的定义域;
(2)求函数f(x)=log (x2+2x+3)的值域.
解析:(1)由,得,
∴函数的定义域为(-1,0)∪(0,2).
(2)∵x2+2x+3=(x+1)2+2≥2,
∴定义域为R.
∴f(x)≤log2=-1,
∴值域为(-∞,-1].
10.设函数f(x)=ln(x2+ax+1)的定义域为A.
(1)若1∈A,-3∉A,求实数a的取值范围;
(2)若函数y=f(x)的定义域为R,求实数a的取值范围.
4
解析:(1)由题意,得,
所以a≥.
故实数a的取值范围为.
(2)由题意,得x2+ax+1>0在R上恒成立,则Δ=a2-4<0,解得-20时,f(x)=logax+1,其图象可以看作f(x)=logax的图象向上平移一个单位而得到的,又因f(x)=loga|x|+1(00时的图象关于y轴对称.
答案:A
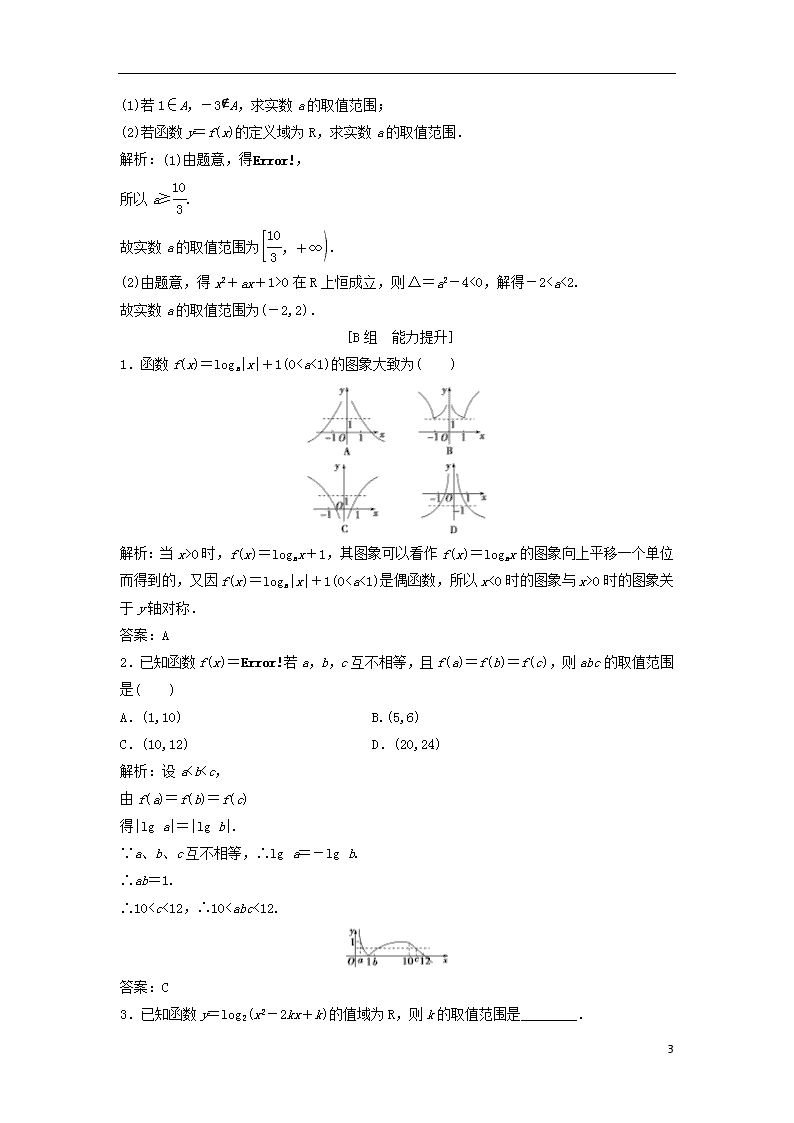
2.已知函数f(x)=若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
A.(1,10) B.(5,6)
C.(10,12) D.(20,24)
解析:设a
查看更多