2014年湖南省高考数学试卷（理科）

2014年湖南省高考数学试卷（理科）

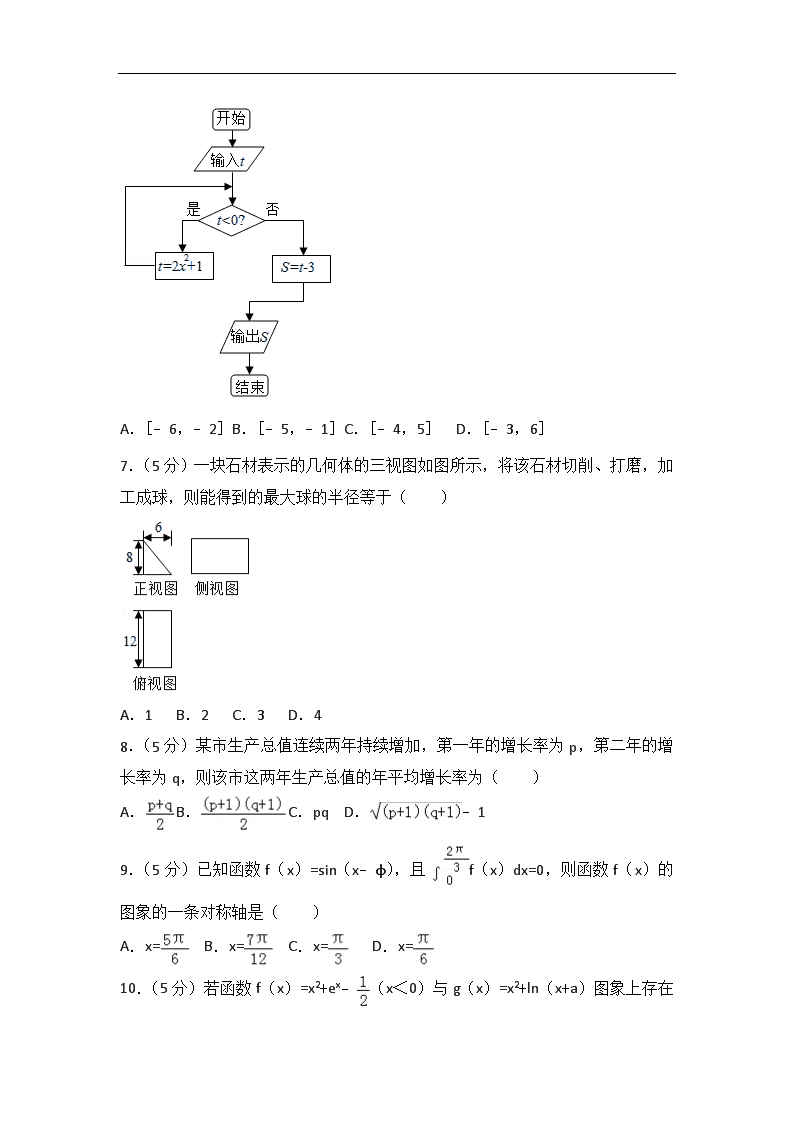
‎2014年湖南省高考数学试卷（理科）‎ ‎　‎ 一、选择题（共10小题，每小题5分，满分50分）‎ ‎1．（5分）满足=i（i为虚数单位）的复数z=（　　）‎ A．+i B．﹣i C．﹣+i D．﹣﹣i ‎2．（5分）对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则（　　）‎ A．P1=P2＜P3 B．P2=P3＜P1 C．P1=P3＜P2 D．P1=P2=P3‎ ‎3．（5分）已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）﹣g（x）=x3+x2+1，则f（1）+g（1）=（　　）‎ A．﹣3 B．﹣1 C．1 D．3‎ ‎4．（5分）（x﹣2y）5的展开式中x2y3的系数是（　　）‎ A．﹣20 B．﹣5 C．5 D．20‎ ‎5．（5分）已知命题p：若x＞y，则﹣x＜﹣y；命题q：若x＞y，则x2＞y2，在命题①p∧q；②p∨q；③p∧（￢q）；④（￢p）∨q中，真命题是（　　）‎ A．①③ B．①④ C．②③ D．②④‎ ‎6．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]，则输出的S属于（　　）‎ A．[﹣6，﹣2] B．[﹣5，﹣1] C．[﹣4，5] D．[﹣3，6]‎ ‎7．（5分）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（　　）‎ A．1 B．2 C．3 D．4‎ ‎8．（5分）某市生产总值连续两年持续增加，第一年的增长率为p，第二年的增长率为q，则该市这两年生产总值的年平均增长率为（　　）‎ A． B． C．pq D．﹣1‎ ‎9．（5分）已知函数f（x）=sin（x﹣φ），且f（x）dx=0，则函数f（x）的图象的一条对称轴是（　　）‎ A．x= B．x= C．x= D．x=‎ ‎10．（5分）若函数f（x）=x2+ex﹣（x＜0）与g（x）=x2+ln（x+‎ a）图象上存在关于y轴对称的点，则a的取值范围是（　　）‎ A．（﹣） B．（） C．（） D．（）‎ ‎　‎ 二、填空题（共3小题，每小题5分，满分10分）（一）选做题（请考生在第11,12,13三题中任选两题作答，如果全做，则按前两题记分）‎ ‎11．（5分）在平面直角坐标系中，倾斜角为的直线l与曲线C：，（α为参数）交于A，B两点，且|AB|=2，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，则直线l的极坐标方程是　 　．‎ ‎12．（5分）如图所示，已知AB，BC是⊙O的两条弦，AO⊥BC，AB=，BC=2，则⊙O的半径等于　 　．‎ ‎13．若关于x的不等式|ax﹣2|＜3的解集为{x|﹣＜x＜}，则a=　 　．‎ ‎　‎ ‎（二）必做题（14-16题）‎ ‎14．（5分）若变量x，y满足约束条件，且z=2x+y的最小值为﹣6，则k=　 　．‎ ‎15．（5分）如图所示，正方形ABCD与正方形DEFG的边长分别为a，b（a＜b），原点O为AD的中点，抛物线y2=2px（p＞0）经过C，F两点，则=　 　．‎ ‎16．（5分）在平面直角坐标系中，O为原点，A（﹣1，0），B（0，），C（3，0），动点D满足||=1，则|++|的最大值是　 　．‎ ‎　‎ 三、解答题：本大题共6小题，共75分 ‎17．（12分）某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为和．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立．‎ ‎（Ⅰ）求至少有一种新产品研发成功的概率；‎ ‎（Ⅱ）若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，求该企业可获利润的分布列和数学期望．‎ ‎18．（12分）如图，在平面四边形ABCD中，AD=1，CD=2，AC=．‎ ‎（Ⅰ）求cos∠CAD的值；‎ ‎（Ⅱ）若cos∠BAD=﹣，sin∠CBA=，求BC的长．‎ ‎19．（12分）如图，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．‎ ‎（Ⅰ）证明：O1O⊥底面ABCD；‎ ‎（Ⅱ）若∠CBA=60°，求二面角C1﹣OB1﹣D的余弦值．‎ ‎20．（13分）已知数列{an}满足a1=1，|an+1﹣an|=pn，n∈N*．‎ ‎（Ⅰ）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；‎ ‎（Ⅱ）若p=，且{a2n﹣1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式．‎ ‎21．（13分）如图，O为坐标原点，椭圆C1：+=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为e1；双曲线C2：﹣=1的左、右焦点分别为F3，F4，离心率为e2，已知e1e2=，且|F2F4|=﹣1．‎ ‎（Ⅰ）求C1、C2的方程；‎ ‎（Ⅱ）过F1作C1的不垂直于y轴的弦AB，M为AB的中点，当直线OM与C2交于P，Q两点时，求四边形APBQ面积的最小值．‎ ‎22．（13分）已知常数a＞0，函数f（x）=ln（1+ax）﹣．‎ ‎（Ⅰ）讨论f（x）在区间（0，+∞）上的单调性；‎ ‎（Ⅱ）若f（x）存在两个极值点x1，x2，且f（x1）+f（x2）＞0，求a的取值范围．‎ ‎　‎ ‎2014年湖南省高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共10小题，每小题5分，满分50分）‎ ‎1．（5分）满足=i（i为虚数单位）的复数z=（　　）‎ A．+i B．﹣i C．﹣+i D．﹣﹣i ‎【分析】根据复数的基本运算即可得到结论．‎ ‎【解答】解：∵=i，‎ ‎∴z+i=zi，‎ 即z===﹣i，‎ 故选：B．‎ ‎【点评】本题主要考查复数的计算，比较基础．‎ ‎　‎ ‎2．（5分）对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则（　　）‎ A．P1=P2＜P3 B．P2=P3＜P1 C．P1=P3＜P2 D．P1=P2=P3‎ ‎【分析】根据简单随机抽样、系统抽样和分层抽样的定义即可得到结论．‎ ‎【解答】解：根据简单随机抽样、系统抽样和分层抽样的定义可知，无论哪种抽样，每个个体被抽中的概率都是相等的，‎ 即P1=P2=P3．‎ 故选：D．‎ ‎【点评】本题主要考查简单随机抽样、系统抽样和分层抽样的性质，比较基础．‎ ‎　‎ ‎3．（5分）已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）﹣g（x）=x3+x2+1，则f（1）+g（1）=（　　）‎ A．﹣3 B．﹣1 C．1 D．3‎ ‎【分析】将原代数式中的x替换成﹣x，再结合着f（x）和g（x）的奇偶性可得f（x）+g（x），再令x=1即可．‎ ‎【解答】解：由f（x）﹣g（x）=x3+x2+1，将所有x替换成﹣x，得 f（﹣x）﹣g（﹣x）=﹣x3+x2+1，‎ 根据f（x）=f（﹣x），g（﹣x）=﹣g（x），得 f（x）+g（x）=﹣x3+x2+1，再令x=1，计算得，‎ f（1）+g（1）=1．‎ 故选：C．‎ ‎【点评】本题属于容易题，是对函数奇偶性的考查，在高考中，函数奇偶性的考查一般相对比较基础，学生在掌握好基础知识的前提下，做题应该没有什么障碍．本题中也可以将原代数式中的x直接令其等于﹣1也可以得到计算结果．‎ ‎　‎ ‎4．（5分）（x﹣2y）5的展开式中x2y3的系数是（　　）‎ A．﹣20 B．﹣5 C．5 D．20‎ ‎【分析】利用二项式定理的展开式的通项公式，求解所求项的系数即可．‎ ‎【解答】解：由二项式定理可知：Tr+1=，‎ 要求解（x﹣2y）5的展开式中x2y3的系数，‎ 所以r=3，‎ 所求系数为：=﹣20．‎ 故选：A．‎ ‎【点评】本题考查二项式定理的通项公式的应用，基本知识的考查．‎ ‎　‎ ‎5．（5分）已知命题p：若x＞y，则﹣x＜﹣y；命题q：若x＞y，则x2＞y2‎ ‎，在命题①p∧q；②p∨q；③p∧（￢q）；④（￢p）∨q中，真命题是（　　）‎ A．①③ B．①④ C．②③ D．②④‎ ‎【分析】根据不等式的性质分别判定命题p，q的真假，利用复合命题之间的关系即可得到结论．‎ ‎【解答】解：根据不等式的性质可知，若若x＞y，则﹣x＜﹣y成立，即p为真命题，‎ 当x=1，y=﹣1时，满足x＞y，但x2＞y2不成立，即命题q为假命题，‎ 则①p∧q为假命题；②p∨q为真命题；③p∧（￢q）为真命题；④（￢p）∨q为假命题，‎ 故选：C．‎ ‎【点评】本题主要考查复合命题之间的关系，根据不等式的性质分别判定命题p，q的真假是解决本题的关键，比较基础．‎ ‎　‎ ‎6．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]，则输出的S属于（　　）‎ A．[﹣6，﹣2] B．[﹣5，﹣1] C．[﹣4，5] D．[﹣3，6]‎ ‎【分析】根据程序框图，结合条件，利用函数的性质即可得到结论．‎ ‎【解答】解：若0≤t≤2，则不满足条件输出S=t﹣3∈[﹣3，﹣1]，‎ 若﹣2≤t＜0，则满足条件，此时t=2t2+1∈（1，9]，此时不满足条件，输出S=t﹣3∈（﹣2，6]，‎ 综上：S=t﹣3∈[﹣3，6]，‎ 故选：D．‎ ‎【点评】本题主要考查程序框图的识别和判断，利用函数的取值范围是解决本题的关键，比较基础．‎ ‎　‎ ‎7．（5分）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（　　）‎ A．1 B．2 C．3 D．4‎ ‎【分析】由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r．‎ ‎【解答】解：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r，则 ‎8﹣r+6﹣r=，‎ ‎∴r=2．‎ 故选：B．‎ ‎【点评】本题考查三视图，考查几何体的内切圆，考查学生的计算能力，属于基础题．‎ ‎　‎ ‎8．（5分）某市生产总值连续两年持续增加，第一年的增长率为p，第二年的增长率为q，则该市这两年生产总值的年平均增长率为（　　）‎ A． B． C．pq D．﹣1‎ ‎【分析】设该市这两年生产总值的年平均增长率为x，可得（1+p）（1+q）=（1+x）2，解出即可．‎ ‎【解答】解：设该市这两年生产总值的年平均增长率为x，‎ 则（1+p）（1+q）=（1+x）2，‎ 解得x=﹣1，‎ 故选：D．‎ ‎【点评】本题考查了指数的运算性质、乘法公式，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎9．（5分）已知函数f（x）=sin（x﹣φ），且f（x）dx=0，则函数f（x）的图象的一条对称轴是（　　）‎ A．x= B．x= C．x= D．x=‎ ‎【分析】由f（x）dx=0求得cos（φ+）=0，故有 φ+=kπ+，k∈z．可取φ=，则f（x）=sin（x﹣）．‎ 令x﹣=kπ+，求得x的值，可得函数f（x）的图象的一条对称轴方程．‎ ‎【解答】解：∵函数f（x）=sin（x﹣φ），‎ f（x）dx=﹣cos（x﹣φ）=﹣cos（﹣φ）﹣[﹣cos（﹣φ）]=cosφ﹣sinφ=cos（φ+）=0，‎ ‎∴φ+=kπ+，k∈z，即 φ=kπ+，k∈z，故可取φ=，f（x）=sin（x﹣）．‎ 令x﹣=kπ+，求得 x=kπ+，k∈Z，‎ 则函数f（x）的图象的一条对称轴为 x=，‎ 故选：A．‎ ‎【点评】本题主要考查定积分，函数y=Asin（ωx+φ）的图象的对称性，两角和差的三角公式的应用，属于中档题．‎ ‎　‎ ‎10．（5分）若函数f（x）=x2+ex﹣（x＜0）与g（x）=x2+ln（x+a）图象上存在关于y轴对称的点，则a的取值范围是（　　）‎ A．（﹣） B．（） C．（） D．（）‎ ‎【分析】由题意可得ex0﹣﹣ln（﹣x0+a）=0有负根，函数h（x）=ex﹣﹣ln（﹣x+a）为增函数，由此能求出a的取值范围．‎ ‎【解答】解：由题意可得：‎ 存在x0∈（﹣∞，0），满足x02+ex0﹣=（﹣x0）2+ln（﹣x0+a），‎ 即ex0﹣﹣ln（﹣x0+a）=0有负根，‎ ‎∵当x趋近于负无穷大时，ex0﹣﹣ln（﹣x0+a）也趋近于负无穷大，‎ 且函数h（x）=ex﹣﹣ln（﹣x+a）为增函数，‎ ‎∴h（0）=e0﹣﹣lna＞0，‎ ‎∴lna＜ln，‎ ‎∴a＜，‎ ‎∴a的取值范围是（﹣∞，），‎ 故选：A．‎ ‎【点评】本题考查的知识点是函数的图象和性质，函数的零点，函数单调性的性质，函数的极限，是函数图象和性质较为综合的应用．‎ ‎　‎ 二、填空题（共3小题，每小题5分，满分10分）（一）选做题（请考生在第11,12,13三题中任选两题作答，如果全做，则按前两题记分）‎ ‎11．（5分）在平面直角坐标系中，倾斜角为的直线l与曲线C：，（α为参数）交于A，B两点，且|AB|=2，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，则直线l的极坐标方程是　ρ（cosθ﹣sinθ）=1　．‎ ‎【分析】由题意可得直线l的方程为y=x+b，曲线方程化为直角坐标，表示一个圆，由于弦长正好等于直径，可得圆心（2，1）在直线l上，由此求得b的值，可得直线的方程．‎ ‎【解答】解：设倾斜角为的直线l的方程为y=x+b，‎ 曲线C：（α为参数），即 （x﹣2）2+（y﹣1）2=1，表示以（2，1）为圆心、半径等于1的圆．‎ 由于弦长|AB|=2，正好等于直径，故圆心（2，1）在直线l上，故有1=2+b，解得b=﹣1，‎ 故直线l的方程为 y=x﹣1，即x﹣y﹣1=0．‎ 再根据极坐标与直角坐标的互化公式可得ρcosθ﹣ρsinθ﹣1=0，即ρ（cosθ﹣sinθ）=1‎ 故答案为：ρ（cosθ﹣sinθ）=1．‎ ‎【点评】本题主要考查把参数方程化为直角坐标方程，直线和圆的位置关系，属于基础题．‎ ‎　‎ ‎12．（5分）如图所示，已知AB，BC是⊙O的两条弦，AO⊥BC，AB=，BC=2，则⊙O的半径等于　1.5　．‎ ‎【分析】设垂足为D，⊙O的半径等于R，先计算AD，再计算R即可．‎ ‎【解答】解：设垂足为D，⊙O的半径等于R，则 ‎∵AB，BC是⊙O的两条弦，AO⊥BC，AB=，BC=2，‎ ‎∴AD=1，‎ ‎∴R2=2+（R﹣1）2，‎ ‎∴R=1.5．‎ 故答案为：1.5‎ ‎【点评】本题考查垂径定理的运用，考查学生的计算能力，属于基础题．‎ ‎　‎ ‎13．若关于x的不等式|ax﹣2|＜3的解集为{x|﹣＜x＜}，则a=　﹣3　．‎ ‎【分析】由题意可得﹣和是|ax﹣2|=3的两个根，故有，由此求得a的值．‎ ‎【解答】解：∵关于x的不等式|ax﹣2|＜3的解集为{x|﹣＜x＜}，‎ ‎∴﹣和是|ax﹣2|=3的两个根，∴，∴a=﹣3，‎ 故答案为：﹣3．‎ ‎【点评】本题主要考查绝对值不等式的解法，体现了分类讨论的数学思想，属于中档题．‎ ‎　‎ ‎（二）必做题（14-16题）‎ ‎14．（5分）若变量x，y满足约束条件，且z=2x+y的最小值为﹣6，则k=　﹣2　．‎ ‎【分析】作出不等式对应的平面区域，利用线性规划的知识，通过平移即先确定z的最优解，然后确定k的值即可．‎ ‎【解答】解：作出不等式对应的平面区域，（阴影部分）‎ 由z=2x+y，得y=﹣2x+z，‎ 平移直线y=﹣2x+z，由图象可知当直线y=﹣2x+z经过点A时，直线y=﹣2x+z的截距最小，此时z最小．‎ 目标函数为2x+y=﹣6，‎ 由，解得，‎ 即A（﹣2，﹣2），‎ ‎∵点A也在直线y=k上，‎ ‎∴k=﹣2，‎ 故答案为：﹣2．‎ ‎【点评】本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．‎ ‎　‎ ‎15．（5分）如图所示，正方形ABCD与正方形DEFG的边长分别为a，b（a＜b），原点O为AD的中点，抛物线y2=2px（p＞0）经过C，F两点，则=　　．‎ ‎【分析】可先由图中的点与抛物线的位置关系，写出C，F两点的坐标，再将坐标代入抛物线方程中，消去参数p后，得到a，b的关系式，再寻求的值．‎ ‎【解答】解：由题意可得，，‎ 将C，F两点的坐标分别代入抛物线方程y2=2px中，得 ‎∵a＞0，b＞0，p＞0，两式相比消去p得，化简整理得a2+2ab﹣b2=0，‎ 此式可看作是关于a的一元二次方程，由求根公式得，‎ 取，‎ 从而，‎ 故答案为：．‎ ‎【点评】本题关键是弄清两个正方形与抛物线的位置关系，这样才能顺利写出C，F的坐标，接下来是消参，得到了一个关于a，b的齐次式，应注意根的取舍与细心的计算．‎ ‎　‎ ‎16．（5分）在平面直角坐标系中，O为原点，A（﹣1，0），B（0，），C（3，0），动点D满足||=1，则|++|的最大值是　+1　．‎ ‎【分析】由题意可得，点D在以C（3，0）为圆心的单位圆上，设点D的坐标为（3+cosθ，sinθ），求得|++|≤|++|+||，可得|++|的最大值．‎ ‎【解答】解：由题意可得，点D在以C（3，0）为圆心的单位圆上，设点D的坐标为（3+cosθ，sinθ），‎ 则|++|≤|++|+||=+1．‎ ‎∴|++|的最大值是 +1，‎ 故答案为：+1．‎ ‎【点评】本题主要考查参数方程的应用，求向量的模，属于中档题．‎ ‎　‎ 三、解答题：本大题共6小题，共75分 ‎17．（12分）某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为和．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立．‎ ‎（Ⅰ）求至少有一种新产品研发成功的概率；‎ ‎（Ⅱ）若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，求该企业可获利润的分布列和数学期望．‎ ‎【分析】（Ⅰ）利用对立事件的概率公式，计算即可，‎ ‎（Ⅱ）求出企业利润的分布列，再根据数学期望公式计算即可．‎ ‎【解答】解：（Ⅰ）设至少有一种新产品研发成功的事件为事件A且事件B为事件A的对立事件，则事件B为一种新产品都没有成功，‎ 因为甲乙研发新产品成功的概率分别为和．‎ 则P（B）=，‎ 再根据对立事件的概率之间的公式可得P（A）=1﹣P（B）=，‎ 故至少有一种新产品研发成功的概率为．‎ ‎（Ⅱ）由题可得设企业可获得利润为X，则X的取值有0，120，100，220，‎ 由独立试验的概率计算公式可得，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 所以X的分布列如下：‎ X ‎0‎ ‎120‎ ‎100‎ ‎220‎ P（x）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 则数学期望E（X）==140．‎ ‎【点评】本题主要考查了对立事件的概率，分布列和数学期望，培养学生的计算能力，也是近几年高考题目的常考的题型．‎ ‎　‎ ‎18．（12分）如图，在平面四边形ABCD中，AD=1，CD=2，AC=．‎ ‎（Ⅰ）求cos∠CAD的值；‎ ‎（Ⅱ）若cos∠BAD=﹣，sin∠CBA=，求BC的长．‎ ‎【分析】（Ⅰ）利用余弦定理，利用已知条件求得cos∠CAD的值．‎ ‎（Ⅱ）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．‎ ‎【解答】解：（Ⅰ）cos∠CAD===．‎ ‎（Ⅱ）∵cos∠BAD=﹣，‎ ‎∴sin∠BAD==，‎ ‎∵cos∠CAD=，‎ ‎∴sin∠CAD==‎ ‎∴sin∠BAC=sin（∠BAD﹣∠CAD）=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD=×+×=，‎ ‎∴由正弦定理知=，‎ ‎∴BC=•sin∠BAC=×=3‎ ‎【点评】本题主要考查了正弦定理和余弦定理的综合运用，三角函数恒等变换的应用．考查了学生对基础知识的综合运用．‎ ‎　‎ ‎19．（12分）如图，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．‎ ‎（Ⅰ）证明：O1O⊥底面ABCD；‎ ‎（Ⅱ）若∠CBA=60°，求二面角C1﹣OB1﹣D的余弦值．‎ ‎【分析】（Ⅰ）由已知中，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．可得O1O∥CC1∥BB1且CC1⊥AC，BB1⊥BD，进而OO1⊥AC，OO1⊥BD，再由线面垂直的判定定理得到O1O⊥底面ABCD；‎ ‎（Ⅱ）设四棱柱ABCD﹣A1B1C1D1的所有棱长均为2a，设AB为2，若∠CBA=60°，OA=OC=1，OB=OD=，以O为坐标原点，分别以OB，OC，OO1为x，y，z轴正方向建立空间直角坐标系，求出平面BDD1B1和平面OB1C1的法向量，代入向量夹角公式，求出二面角的余弦值．‎ ‎【解答】证明：（Ⅰ）∵四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，‎ ‎∴四边形ABCD为菱形，‎ 又∵AC∩BD=O，‎ 故O为BD的中点，‎ 同理O1也是B1D1的中点，‎ 又∵四边形ACC1A1和四边形BDD1B1均为矩形，‎ ‎∴O1O∥CC1∥BB1且CC1⊥AC，BB1⊥BD，‎ ‎∴OO1⊥AC，OO1⊥BD，‎ 又∵AC∩BD=O，AC，BD⊂平面ABCD，‎ ‎∴O1O⊥底面ABCD；‎ 解：（Ⅱ）设四棱柱ABCD﹣A1B1C1D1的所有棱长均相等，所以四边形ABCD是菱形，‎ ‎∴AC⊥BD，‎ 又∵O1O⊥底面ABCD，‎ ‎∴OB，OC，OO1两两垂直，‎ 如图，以O为坐标原点，OB，OC，OO1所在直线分别为x轴，y轴，z轴建立直角坐标系O﹣xyz．‎ 设AB=2，‎ ‎∵∠CBA=60°，‎ ‎∴OA=OC=1，OB=OD=，‎ 则O（0，0，0），B1（），C1（0，1，2）‎ 易知，=（0，1，0）是平面BDD1B1的一个法向量，‎ 设=（x，y，z）是平面OB1C1的一个法向量，则，即 取z=﹣，则x=2，y=2，所以=（2，2，﹣）‎ 设二面角C1﹣OB1﹣D的大小为θ，易知θ是锐角，于是：‎ cosθ=|cos＜，＞|=||==，‎ 故二面角C1﹣OB1﹣D的余弦值为．‎ ‎【点评】本题考查的知识点是空间二面角的平面角，建立空间坐标系，将二面角问题转化为向量夹角问题，是解答的关键．‎ ‎　‎ ‎20．（13分）已知数列{an}满足a1=1，|an+1﹣an|=pn，n∈N*．‎ ‎（Ⅰ）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；‎ ‎（Ⅱ）若p=，且{a2n﹣1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式．‎ ‎【分析】（Ⅰ）根据条件去掉式子的绝对值，分别令n=1，2代入求出a2和a3，再由等差中项的性质列出关于p的方程求解，利用“{an}是递增数列”对求出的p的值取舍；‎ ‎（Ⅱ）根据数列的单调性和式子“|an+1﹣an|=pn”、不等式的可加性，求出和a2n+1﹣a2n=，再对数列{an}的项数分类讨论，利用累加法和等比数列前n项和公式，求出数列{an}的奇数项、偶数项对应的通项公式，再用分段函数的形式表示出来．‎ ‎【解答】解：（Ⅰ）∵数列{an}是递增数列，∴an+1﹣an＞0，‎ 则|an+1﹣an|=pn化为：an+1﹣an=pn，‎ 分别令n=1，2可得，a2﹣a1=p，，‎ 即a2=1+p，，‎ ‎∵a1，2a2，3a3成等差数列，∴4a2=a1+3a3，‎ 即4（1+p）=1+3（p2+p+1），‎ 化简得3p2﹣p=0，解得或0，‎ 当p=0时，数列an为常数数列，不符合数列{an}是递增数列，‎ ‎∴；‎ ‎（2）由题意可得，|an+1﹣an|=，‎ 则|a2n﹣a2n﹣1|=，|a2n+2﹣a2n+1|=，‎ ‎∵数列{a2n﹣1}是递增数列，且{a2n}是递减数列，‎ ‎∴a2n+1﹣a2n﹣1＞0，且a2n+2﹣a2n＜0，‎ 则﹣（a2n+2﹣a2n）＞0，两不等式相加得 a2n+1﹣a2n﹣1﹣（a2n+2﹣a2n）＞0，即a2n+1﹣a2n+2＞a2n﹣1﹣a2n，‎ 又∵|a2n﹣a2n﹣1|=＞|a2n+2﹣a2n+1|=，‎ ‎∴a2n﹣a2n﹣1＞0，即，‎ 同理可得：a2n+3﹣a2n+2＞a2n+1﹣a2n，即|a2n+3﹣a2n+2|＜|a2n+1﹣a2n|，‎ 则a2n+1﹣a2n=‎ 当数列{an}的项数为偶数时，令n=2m（m∈N*），‎ ‎，，，…，，‎ 这2m﹣1个等式相加可得，‎ ‎==，‎ 则；‎ 当数列{an}的项数为奇数时，令n=2m+1（m∈N*）‎ ‎，，，…，，‎ 这2m个等式相加可得，…﹣…+‎ ‎=﹣=，‎ 则，且当m=0时a1=1符合，‎ 故，‎ 综上得，．‎ ‎【点评】本题考查了等差数列的通项公式，等比数列前n项和公式、数列的单调性，累加法求数列的通项公式，不等式的性质等，同时考查数列的基础知识和化归、分类整合等数学思想，以及推理论证、分析与解决问题的能力．本题设计巧妙，题型新颖，立意深刻，是一道不可多得的好题，难度很大．‎ ‎　‎ ‎21．（13分）如图，O为坐标原点，椭圆C1：+=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为e1；双曲线C2：﹣=1的左、右焦点分别为F3，F4，离心率为e2，已知e1e2=，且|F2F4|=﹣1．‎ ‎（Ⅰ）求C1、C2的方程；‎ ‎（Ⅱ）过F1作C1的不垂直于y轴的弦AB，M为AB的中点，当直线OM与C2交于P，Q两点时，求四边形APBQ面积的最小值．‎ ‎【分析】（Ⅰ）由斜率公式写出e1，e2，把双曲线的焦点用含有a，b的代数式表示，结合已知条件列关于a，b的方程组求解a，b的值，则圆锥曲线方程可求；‎ ‎（Ⅱ）设出AB所在直线方程，和椭圆方程联立后得到关于y的一元二次方程，由根与系数的关系得到AB中点M的坐标，并由椭圆的焦点弦公式求出AB的长度，写出PQ的方程，和双曲线联立后解出P，Q的坐标，由点到直线的距离公式分别求出P，Q到AB的距离，然后代入代入三角形面积公式得四边形APBQ的面积，再由关于n的函数的单调性求得最值．‎ ‎【解答】解：（Ⅰ）由题意可知，，且．‎ ‎∵e1e2=，且|F2F4|=﹣1．‎ ‎∴，且．‎ 解得：．‎ ‎∴椭圆C1的方程为，双曲线C2的方程为；‎ ‎（Ⅱ）由（Ⅰ）可得F1（﹣1，0）．‎ ‎∵直线AB不垂直于y轴，‎ ‎∴设AB的方程为x=ny﹣1，‎ 联立，得（n2+2）y2﹣2ny﹣1=0．‎ 设A（x1，y1），B（x2，y2），M（x0，y0），‎ 则，．‎ 则 ‎==．‎ ‎∵M在直线AB上，‎ ‎∴．‎ 直线PQ的方程为，‎ 联立，得．‎ 解得，代入 得．‎ 由2﹣n2＞0，得﹣＜n＜．‎ ‎∴P，Q的坐标分别为，‎ 则P，Q到AB的距离分别为：，．‎ ‎∵P，Q在直线A，B的两端，‎ ‎∴．‎ 则四边形APBQ的面积S=|AB|．‎ ‎∴当n2=0，即n=0时，四边形APBQ面积取得最小值2．‎ ‎【点评】本题考查圆锥曲线方程的求法，是直线与圆锥曲线、圆锥曲线与圆锥曲线间的关系的综合题，考查了椭圆与双曲线的基本性质，关键是学生要有较强的运算能力，是压轴题．‎ ‎　‎ ‎22．（13分）已知常数a＞0，函数f（x）=ln（1+ax）﹣．‎ ‎（Ⅰ）讨论f（x）在区间（0，+∞）上的单调性；‎ ‎（Ⅱ）若f（x）存在两个极值点x1，x2，且f（x1）+f（x2）＞‎ ‎0，求a的取值范围．‎ ‎【分析】（Ⅰ）利用导数判断函数的单调性，注意对a分类讨论；‎ ‎（Ⅱ）利用导数判断函数的极值，注意a的讨论及利用换元法转化为求函数最值问题解决．‎ ‎【解答】解：（Ⅰ）∵f（x）=ln（1+ax）﹣．‎ ‎∴f′（x）==，‎ ‎∵（1+ax）（x+2）2＞0，∴当1﹣a≤0时，即a≥1时，f′（x）≥0恒成立，则函数f（x）在（0，+∞）单调递增，‎ 当0＜a≤1时，由f′（x）=0得x=±，则函数f（x）在（0，）单调递减，在（，+∞）单调递增．‎ ‎（Ⅱ）由（Ⅰ）知，当a≥1时，f′（x）≥0，此时f（x）不存在极值点．‎ 因此要使f（x）存在两个极值点x1，x2，则必有0＜a＜1，又f（x）的极值点值可能是x1=，x2=﹣，‎ 且由f（x）的定义域可知x＞﹣且x≠﹣2，‎ ‎∴﹣＞﹣且﹣≠﹣2，解得a≠，则x1，x2分别为函数f（x）的极小值点和极大值点，‎ ‎∴f（x1）+f（x2）=ln[1+ax1]﹣+ln（1+ax2）﹣=ln[1+a（x1+x2）+a2x1x2]﹣‎ ‎=ln（2a﹣1）2﹣=ln（2a﹣1）2+﹣2．‎ 令2a﹣1=x，由0＜a＜1且a≠得，‎ 当0＜a＜时，﹣1＜x＜0；当＜a＜1时，0＜x＜1．‎ 令g（x）=lnx2+﹣2．‎ ‎（i）当﹣1＜x＜0时，g（x）=2ln（﹣x）+﹣2，∴g′（x）=﹣=＜0，‎ 故g（x）在（﹣1，0）上单调递减，g（x）＜g（﹣1）=﹣4＜0，‎ ‎∴当0＜a＜时，f（x1）+f（x2）＜0；‎ ‎（ii）当0＜x＜1．g（x）=2lnx+﹣2，g′（x）=﹣=＜0，‎ 故g（x）在（0，1）上单调递减，g（x）＞g（1）=0，‎ ‎∴当＜a＜1时，f（x1）+f（x2）＞0；‎ 综上所述，a的取值范围是（，1）．‎ ‎【点评】本题主要考查学生对含有参数的函数的单调性及极值的判断，考查利用导数判断函数的单调性及求极值的能力，考查分类讨论思想及转化划归思想的运用和运算能力，逻辑性综合性强，属难题．‎ ‎　‎