- 2021-06-30 发布 |
- 37.5 KB |
- 14页

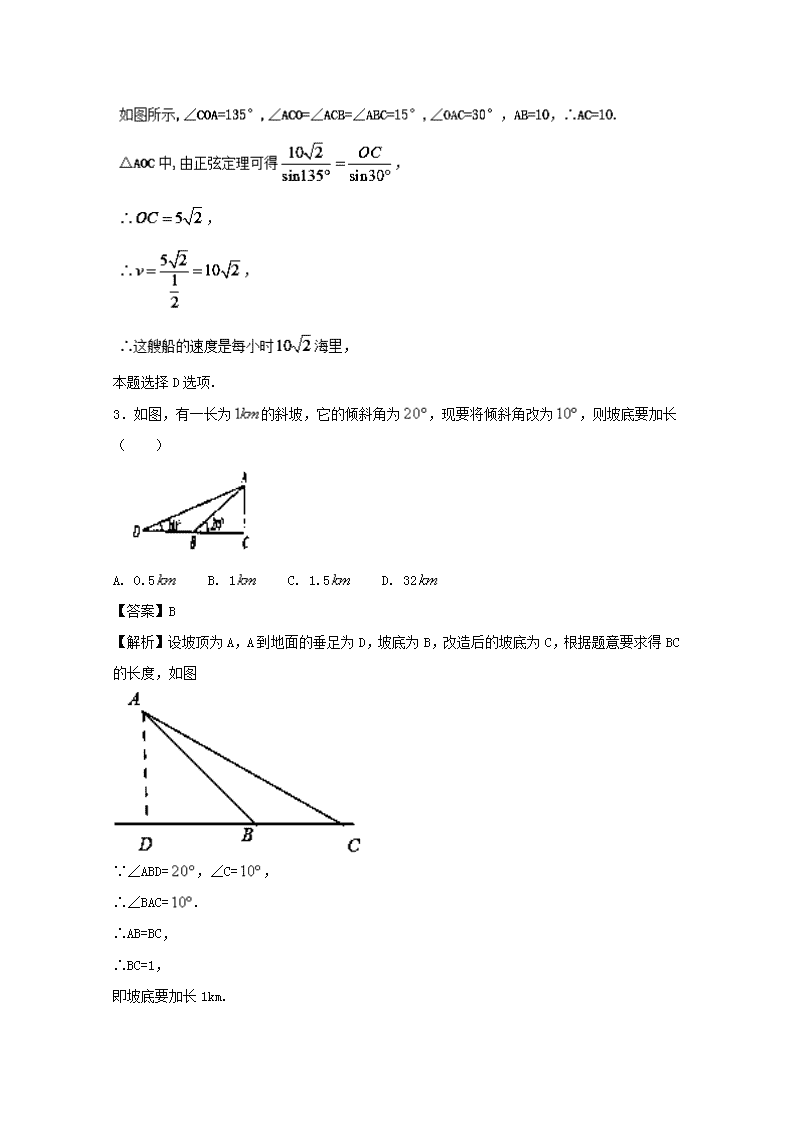
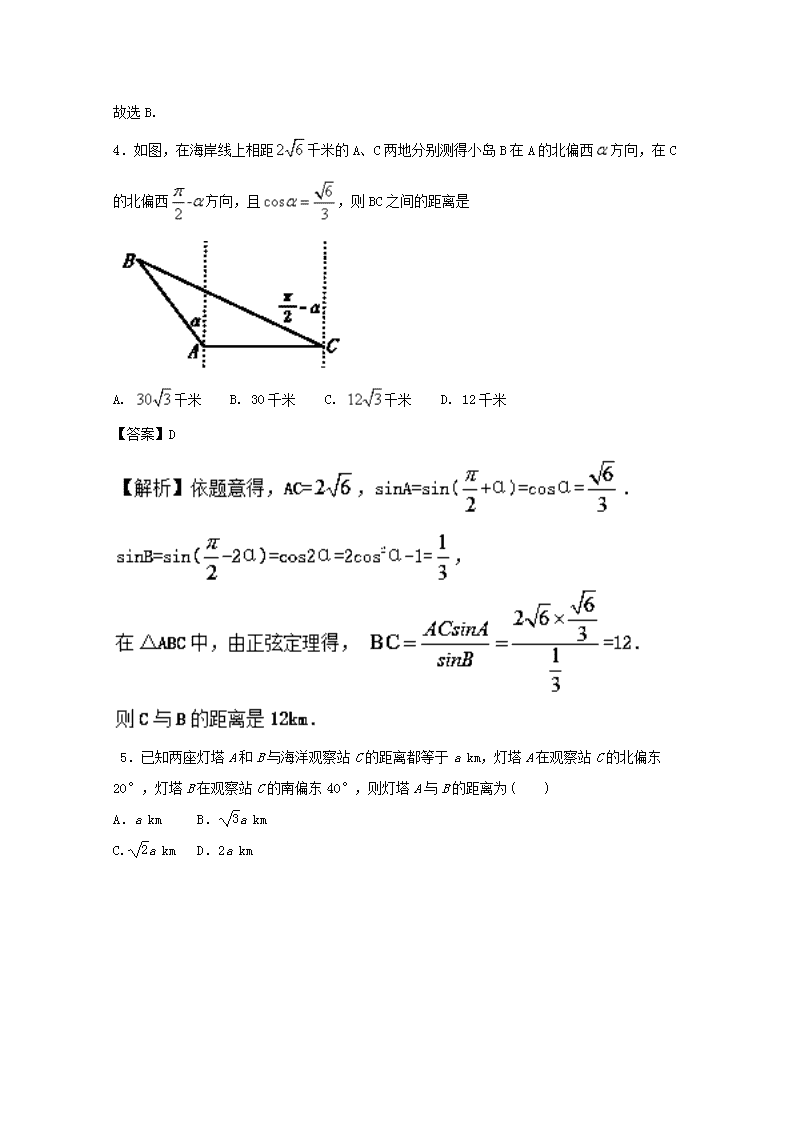
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题4-7 解三角形及其应用举例(测)-2018年高考数学一轮复习讲练测(浙江版)
第07节 解三角形及其应用举例 班级__________ 姓名_____________ 学号___________ 得分__________ 一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的。) 1.海上两小岛到海洋观察站的距离都是,小岛在观察站的北偏东,小岛在观察站的南偏东,则与的距离是( ) A. B. C. D. 【答案】C 则AB==10km. 故选:C. 2.一船沿北偏西方向航行,正东有两个灯塔A,B, 海里,航行半小时后,看见一灯塔在船的南偏东,另一灯塔在船的南偏东,则这艘船的速度是每小时 ( ) A. 5海里 B. 海里 C. 10海里 D. 海里 【答案】B 【解析】 本题选择D选项. 3.如图,有一长为的斜坡,它的倾斜角为,现要将倾斜角改为,则坡底要加长( ) A. 0.5 B. 1 C. 1.5 D. 32 【答案】B 【解析】设坡顶为A,A到地面的垂足为D,坡底为B,改造后的坡底为C,根据题意要求得BC的长度,如图 ∵∠ABD=,∠C=, ∴∠BAC=. ∴AB=BC, ∴BC=1, 即坡底要加长1km. 故选B. 4.如图,在海岸线上相距千米的A、C两地分别测得小岛B在A的北偏西方向,在C的北偏西方向,且,则BC之间的距离是 A. 千米 B. 30千米 C. 千米 D. 12千米 【答案】D 5.已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( ) A.a km B.a km C.a km D.2a km 【答案】B 【解析】由图可知,∠ACB=120°, 由余弦定理,得cos ∠ACB===-. 解得AB=a (km). 6.两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站北偏东40°,灯塔B在观察站的南偏东60°,则灯塔A在灯塔B的( ) A.北偏东10° B.北偏西10° C.南偏东10° D.南偏西10° 【答案】 B 7.如图所示,设A、B两点在河的两岸,一测量者在A所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,就可以计算A、B两点的距离为 ( ) A.50m B.50m C.25m D.m 【答案】 A 【解析】由题意知∠ABC=30°,由正弦定理=,∴AB===50(m). 8.已知A、B两地间的距离为10km,B、C两地间的距离为20km,现测得∠ABC=120°,则A、C两地间的距离为( ) A.10km B.km C.10km D.10km 【答案】 D 9.一船向正北航行,看见正西方向有相距10n mile的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这只船的速度是每小时( ) A.5n mile B.5n mile C.10n mile D.10n mile 【答案】 C 【解析】依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10,在直角三角形ABC中,可得AB=5,于是这只船的速度是=10(n mile/h). 10.为测量某塔AB的高度,在一幢与塔AB相距20m的楼顶D处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是( ) A.20m B.20m C.20(1+)m D.30m 【答案】 A 【解析】如图所示,四边形CBMD为正方形,而CB=20(m),所以BM=20(m). 又在Rt△AMD中,DM=20m,∠ADM=30°, ∴AM=DMtan30°=(m), ∴AB=AM+MB=+20=20(m). 11.已知A船在灯塔C北偏东80°处,且A到C距离为2km,B船在灯塔C北偏西40°,AB两船距离为3km,则B到C的距离为( ) A.km B.(-1)km C.(+1)km D.km 【答案】 B 12.一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距塔68n mile的M处,下午2时到达这座灯塔的东南方向的N处,则这只船的航行速度为( ) A.n mile/h B.34n mile/h C.n mile/h D.34n mile/h 【答案】 A 【解析】如图所示,在△PMN中,=, ∴MN==34,∴v==(n mile/h). 二、填空题(本大题共4小题,每小题5分,共20分。把答案填在题中的横线上。) 13.如图,一船自西向东匀速航行,上午10时到达一座灯塔的南偏西,距灯塔68海里的处,下午2时到达这座灯塔的东南方向处,则该船航行的速度为__________海里/小时. 【答案】 【解析】 14.甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东30°角方向直线航行,并1小时后与乙船在C处相遇,则甲船的航速为_________海里/小时。 【答案】17.3 【解析】 设甲船的航速为海里/小时,则,由正弦定理可得海里/小时,故答案为. 15.【2017湖南百所重点中学诊断】我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为13里,14里,15里,假设1里按500米计算,则该沙田的面积为__________平方千米. 【答案】21 16. 如图,一栋建筑物的高为(30-10)m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面点M(B,M,D三点共线)处测得楼顶A,塔顶C的仰角分别为15°和60°,在楼顶A处测得塔顶C的仰角为30°,则通信塔CD的高为________ m. 【答案】60 故答案为60. 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 如图,我军军舰位于岛屿的南偏西方向的B处,且与岛屿相距6海里,海盗船以10海里/小时的速度从岛屿出发沿正北方逃跑,若我军军舰从处出发沿北偏东的方向以14海里/小时的速度追赶海盗船. (Ⅰ)求我军军舰追上海盗船的时间; (Ⅱ)求的值. 【答案】(Ⅰ)我军军舰追上海盗船的时间为1小时;(Ⅱ) . (Ⅱ)在中,因为, , , , 由正弦定理,得, 即 , . 18. 如图,错误!未找到引用源。是两个小区所在地,错误!未找到引用源。到一条公路错误!未找到引用源。的垂直距离分别为错误!未找到引用源。,错误!未找到引用源。两端之间的距离为错误!未找到引用源。. (1)某移动公司将在错误!未找到引用源。之间找一点错误!未找到引用源。,在错误!未找到引用源。处建造一个信号塔,使得错误!未找到引用源。对错误!未找到引用源。的张角与错误!未找到引用源。对错误!未找到引用源。的张角相等,试确定点错误!未找到引用源。的位置; (2)环保部门将在错误!未找到引用源。之间找一点错误!未找到引用源。,在错误!未找到引用源。处建造一个垃圾处理厂,使得错误!未找到引用源。对错误!未找到引用源。所张角最大,试确定点错误!未找到引用源。的位置. 【答案】(1)4;(2)错误!未找到引用源。. 【解析】试题分析: (1)利用张角相等的相似性即可确定点P的位置; (2)由题意得到三角函数,换元之后结合对勾函数的性质可得当错误!未找到引用源。时满足题意. 试题解析: (1)张角相等,∴错误!未找到引用源。,∴错误!未找到引用源。 (2)设错误!未找到引用源。,∴错误!未找到引用源。, ∴错误!未找到引用源。,错误!未找到引用源。,错误!未找到引用源。 错误!未找到引用源。,设错误!未找到引用源。,错误!未找到引用源。,错误!未找到引用源。,错误!未找到引用源。, ∴错误!未找到引用源。 错误!未找到引用源。,错误!未找到引用源。, 当且仅当错误!未找到引用源。时,等号成立,此时错误!未找到引用源。,即错误!未找到引用源。 19.如图,在某海滨城市错误!未找到引用源。附近的海面上正形成台风。据气象部门检测,目前台风中心位于城市错误!未找到引用源。的南偏东错误!未找到引用源。方向错误!未找到引用源。的海面错误!未找到引用源。处,并以错误!未找到引用源。的速度向北偏西错误!未找到引用源。方向移动.如果台风侵袭的范围为圆心区域,目前圆形区域的半径为错误!未找到引用源。,并以错误!未找到引用源。的速度不断增大.几小时后该城市开始受到台风侵袭(精确到错误!未找到引用源。)? 【答案】4.1小时. 解:根据题意可设错误!未找到引用源。小时后台风中心到达错误!未找到引用源。点, 答:大约4.1小时后该城市开始受到台风的侵袭。 20.【2018届江苏南京溧水高级中学期初模拟】如图,在海岸线一侧处有一个美丽的小岛,某旅游公司为方便游客,在上设立了两个报名点,满足中任意两点间的距离为.公司拟按以下思路运作:先将两处游客分别乘车集中到之间的中转点处(点异于两点),然后乘同一艘轮游轮前往岛.据统计,每批游客处需发车2辆, 处需发车4辆,每辆汽车每千米耗费元,游轮每千米耗费元.(其中是正常数)设∠,每批游客从各自报名点到岛所需运输成本为元. (1) 写出关于的函数表达式,并指出的取值范围; (2) 问:中转点距离处多远时, 最小? 【答案】(1) ;(2). 【解析】试题分析:(1)在中,求出相关的角,利用正弦定理,求出,表示出所需运输成本为元关于的函数表达式;(2)利用函数表达式,求出函数的导数,通过导数的符号,判断单调性求解函数的最值. 试题解析:(1) 由题知在△ACD中,∠CAD=,∠CDA=α,AC=10,∠ACD=-α. 由正弦定理知, 即CD=, AD=, 所以S=4aAD+8aBD+12aCD= (12CD-4AD+80)a =a+80a =a+60a 所以中转点C距A处km时,运输成本S最小.查看更多