天津市南开中学滨海生态城学校2019-2020学年高二下学期月考数学试卷

天津市南开中学滨海生态城学校2019-2020学年高二下学期月考数学试卷

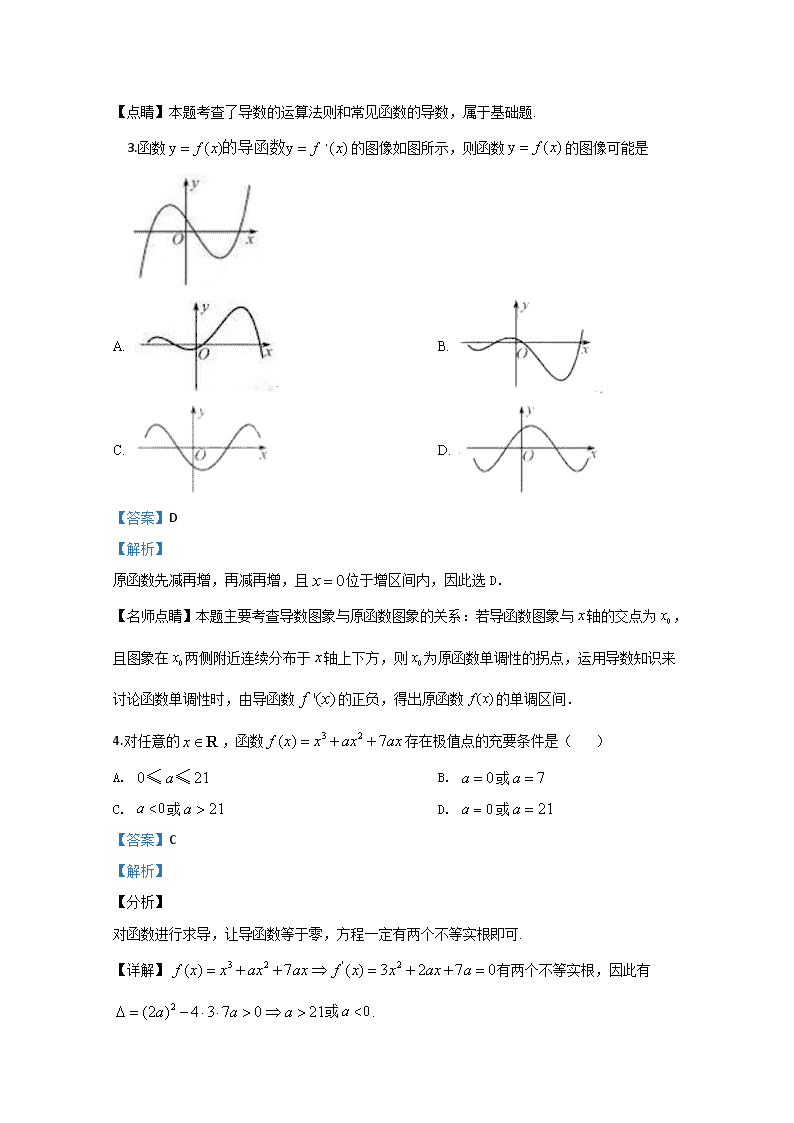
南开中学滨海生态城学校2019-2020（下）‎ 高二年级阶段性反馈数学试卷 一、单选题（每题5分，共15个小题）‎ ‎1.已知a为函数的极小值点，则a=（ ）‎ A. 3 B. －‎2 ‎C. 4 D. 2‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 对函数进行求导，让导函数等于零，解方程，然后利用极小值点的定义进行验证即可.‎ ‎【详解】.‎ 当时，，因此函数单调递增，当时，，因此函数单调递减，当时，，因此函数单调递增，所以是函数的极小值点，故.‎ 故选：A ‎【点睛】本题考查了求函数的极小值点，属于基础题.‎ ‎2.下列导数运算正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据导数的运算法则和常见函数的导数进行判断即可.‎ ‎【详解】A：，故本选项运算不正确；‎ B：，故本选项运算不正确；‎ C：，故本选项运算正确；‎ D：，故本选项运算不正确.‎ 故选：C ‎【点睛】本题考查了导数的运算法则和常见函数的导数，属于基础题.‎ ‎3.函数的图像如图所示，则函数的图像可能是 A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ 原函数先减再增，再减再增，且位于增区间内，因此选D．‎ ‎【名师点睛】本题主要考查导数图象与原函数图象的关系：若导函数图象与轴的交点为，且图象在两侧附近连续分布于轴上下方，则为原函数单调性的拐点，运用导数知识来讨论函数单调性时，由导函数的正负，得出原函数的单调区间．‎ ‎4.对任意的，函数存在极值点的充要条件是（ ）‎ A. B. 或 C. 或 D. 或 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 对函数进行求导，让导函数等于零，方程一定有两个不等实根即可.‎ ‎【详解】有两个不等实根，因此有 或.‎ 故选：C ‎【点睛】本题考查了函数有极值的充要条件的判断，属于基础题.‎ ‎5.若函数有唯一一个极值点，则实数a的取值范围是（ ）‎ A. B. 或 C. D. 或 ‎【答案】C ‎【解析】‎ 分析】‎ 函数有唯一一个极值点，则导函数有唯一大于0的变号零点，画出的图像，使得两个函数图像有唯一一个交点，并且交点的横坐标大于0，故，可求解.‎ ‎【详解】函数有唯一一个极值点，则导函数有唯一的大于0的变号零点，，变形为 ‎ 画出的图像 使得两个函数图像有唯一一个交点，并且交点的横坐标大于0，故，化简为 ‎ 故答案为C.‎ ‎【点睛】‎ 这个题目考查了函数极值点的概念，以及已知函数零点个数求参数范围的问题，已知函数零点(方程根)的个数，求参数取值范围的三种常用的方法：(1)直接法，直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法，先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法，先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．一是转化为两个函数的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为的交点个数的图象的交点个数问题．‎ ‎6.设，则等于（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据导数的定义，结合导数的运算法则进行求解即可.‎ ‎【详解】因为，所以.‎ 故选：D ‎【点睛】本题考查了导数的定义，考查导数的运算法则，属于基础题.‎ ‎7.在曲线上切线倾斜角为的点是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 设出曲线上的点，对函数进行求导，利用导数的几何意义，结合直线斜率与倾斜角之间的关系求解即可.‎ ‎【详解】设曲线上一点的坐标为：，由.‎ 由题意可知：，所以点的坐标为：.‎ 故选：C ‎【点睛】本题考查导数的几何意义，考查了直线倾斜角与斜率之间的关系，考查了数学运算能力.‎ ‎8.函数的导数是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 故选A ‎9.设f(x)，g(x)是定义在R上的恒大于0的可导函数，且，则当时有（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据选项中不等式的结构特征，结合已知的不等式特征，构造新函数，求导，最后利用新构造函数的单调性进行求解即可.‎ ‎【详解】构造函数：，，所以函数定义在R上减函数，当时，有，f(x)，g(x)是定义在R上的恒大于0的函数，所以有.‎ 故选：D ‎【点睛】本题考查了利用导数判断函数的单调性，考查了利用函数单调性判断函数值之间的大小关系，考查了构造法，属于中档题.‎ ‎10.已知函数，若有三个极值点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 对函数进行求导，然后让导函数等于零，根据题意该方程有三个不等正实根，这样通过构造函数，利用单调性进行求解即可.‎ ‎【详解】函数的定义域为：.，显然方程必有一个根为，由题意可知：方程必有两个不等于1的正实根，‎ ‎，令，当时，单调递增，当时，单调递减，故，因此有.‎ 故选：A ‎【点睛】本题考查了已知函数的极值点的个数求参数取值范围，考查了导数的应用，考查了常变量分离法，考查了数学运算能力.‎ ‎11.若关于的方程有实数根，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 把方程进行常变量分离，构造新函数，求导，判断出函数单调性，再根据函数的正负性，画出函数图象，利用数形结合进行求解即可.‎ ‎【详解】，当时，无实数解，不符合题意，故 ‎.‎ 于是有，令，显然当时，；当时，.‎ ‎，当时，，函数单调递减，当时，，函数单调递增，‎ 因此当时，，函数的图象一致如下图所示：‎ 因此要想有实数根，只需方程组：有交点，如上图，则有实数的取值范围是.‎ 故选：D ‎【点睛】本题考查了方程有根求参数取值范围问题，考查了导数的应用，考查了数学运算能力和数形结合能力.‎ ‎12.若函数在区间内是增函数，则实数 的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ ‎，再分类讨论和两种情况，再对满足条件的取并集即可．‎ ‎【详解】‎ 当时，恒成立，即在R上单调递增，满足条件．‎ 当时， 解得，又在区间内是增函数，即 ．‎ 综上所述 故选: B ‎【点睛】此题考查定区间单调求参数取值范围题型，用到的方法为分类讨论，属于一般性题目．‎ ‎13.函数上不单调的一个充分不必要条件是 A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 先求出函数的导函数，再根据函数f（x）在（1，3）上不单调，得g（1）·g（3）＜0且△≥0，从而可求a的取值范围．‎ ‎【详解】‎ 所以 ‎ 令 因为函数上不单调 即在上由实数根 a=0时，显然不成立，‎ a≠0时，只需 ，解得或 ‎ 即a∈‎ 它的充分不必要条件即为一个子集 所以选A ‎【点睛】本题考查了导数的应用，函数的单调性与充分必要条件的综合，属于中档题．‎ ‎14.若函数在区间上有最小值，则实数a的取值范围是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 对函数进行求导，求出函数的单调区间，结合已知条件进行求解即可.‎ ‎【详解】，‎ 当时，单调递减，当时，单调递增，‎ 当时，单调递减，因此函数的极小值为：‎ 或 要想函数区间上有最小值，则有：‎ ‎.‎ 故选：A ‎【点睛】本题考查了函数在区间有最小值求参数取值范围，考查了导数的应用，考查了数学运算能力.‎ ‎15.直线与曲线相切也与曲线相切，则称直线为曲线和曲线的公切线，已知函数，其中，若曲线和曲线的公切线有两条，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 设切点求出两个函数的切线方程，根据这个两个方程表示同一直线，可得方程组，化简方程组，可以得到变量关于其中一个切点横坐标的函数形式，求导，求出函数的单调性，结合该函数的正负性，画出图象图形，最后利用数形结合求出的取值范围.‎ ‎【详解】设曲线的切点为：，，所以过该切点的切线斜率为，因此过该切点的切线方程为：；‎ 设曲线的切点为：，，所以过该切点的切线斜率为，因此过该切点的切线方程为：，则两曲线的公切线应该满足：，‎ 构造函数,‎ 当时，单调递减，当时，‎ 单调递增，所以函数有最大值为：，当时，，当，，函数的图象大致如下图所示：‎ 要想有若曲线和曲线的公切线有两条，则的取值范围为.‎ 故选：C ‎【点睛】本题考查了两个曲线的公切线的条数求参数问题，考查了导数的应用，考查了数学运算能力和数形结合思想.‎ 二、填空题（每小题5分共10小题）‎ ‎16.已知曲线的一条切线的斜率为1，则切点的横坐标为_______‎ ‎【答案】1‎ ‎【解析】‎ ‎【分析】‎ 设出切点的横坐标，求函数的导数，根据导数的几何意义进行求解即可.‎ ‎【详解】设出切点的横坐标为，由.‎ 故答案为：1‎ ‎【点睛】本题考查了导数的几何意义，考查了导数的运算法则，考查了数学运算能力.‎ ‎17.已知函数，则过点可以作出________条图象的切线.‎ ‎【答案】二 ‎【解析】‎ ‎【分析】‎ 设出曲线的切点坐标，对函数求导，利用导数的几何意义，求出切线方程，把点坐标代入切线方程中，求出方程的根进行判断即可.‎ ‎【详解】设切点的坐标为：，，因此切线方程为：，把的坐标代入切线方程中，化简得：或，所以过点可以作出二条的切线.‎ 故答案为：二 ‎【点睛】本题考查了曲线切线的条数问题，考查了导数的几何意义，考查了数学运算能力.‎ ‎18.函数 的定义域为 ，导函数 在内的图象如图所示，则函数在内有极小值点的个数为________．‎ ‎【答案】1‎ ‎【解析】‎ 试题分析：因为函数的极小值两侧导函数值需左负右正；‎ 而由图得：满足导函数值左负右正的自变量只有一个；‎ 故原函数的极小值点只有一个．‎ 考点：利用导数研究函数的极值 ‎19.函数，若对于区间[－2,2]上的任意，，都有，则实数的最小值是_______.‎ ‎【答案】4‎ ‎【解析】‎ ‎【分析】‎ 对函数进行求导，求出函数的单调性，求出函数在区间[－2,2]‎ 上的最值，结合绝对值的性质求出的最大值，最后求出实数的最小值.‎ ‎【详解】，‎ 当时，单调递增，当时，单调递减，‎ 当时，单调递增，因此函数的极小值为：，函数的极大值为，，所以函数在区间[－2,2]上的值域为：，因此对于区间[－2,2]上的任意，，‎ ‎，因此实数的最小值是4.‎ 故答案为：4‎ ‎【点睛】本题考查了不等式恒成立求参数取值范围问题，考查了利用导数求闭区间上函数的最值，考查了绝对值的性质，考查了对任意性的理解，考查了数学运算能力.‎ ‎20.设函数的导数为，且，则=______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 对求导，可得，将代入上式即可求得：，即可求得，将代入即可得解 ‎【详解】因为，所以.‎ 所以，则，‎ 所以 则，‎ 故.‎ ‎【点睛】本题主要考查了导数的运算及赋值法，考查方程思想及计算能力，属于中档题．‎ ‎21.函数的单调递减区间是_______．‎ ‎【答案】 ‎ ‎【解析】‎ 函数的定义域为 ，且： ，‎ 求解不等式 可得函数的单调递减区间是 .‎ ‎22.已知,若存在 ,, 使得成立,则实数的取值范围是_____.‎ ‎【答案】‎ ‎【解析】‎ 试题分析：分两步求解，要使得成立，则有，利用导数研究其单调性求得最小值；要满足使得成立，应有，根据二次函数知识求出最大值，从而得到关于的不等式，求得其范围.‎ 试题解析：，当时，函数递增；当时，函数递减，所以当时，取得极小值即最小值. 函数的最大值为,若，使得成立,则有的最大值大于或等于的最小值,即.‎ 考点：存在性量词与不等式的有解问题．‎ ‎【方法点睛】本题主要考查了存在性量词与不等式的有解问题，属于中档题.含有存在性量词的命题通常转化为有解问题，进一步转化为函数的最值来解答.本题解答的难点是含有两个量词，解答时，先把其中一个函数看成参数，研究另一个的最值，再来解决另一个的最值，从而得到要求参数的不等式，求得其范围.‎ ‎23.已知函数，则不等式的解集为_________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 先判断函数奇偶性，再利用导数判断函数在（0，+∞）上的单调性，再利用函数的奇偶性和单调性解不等式.‎ ‎【详解】由题得f(-x)=,‎ 所以函数f(x)是奇函数.‎ 设x＞0，则，‎ 所以上恒成立，所以函数f(x)在（0，+∞）上单调递增，‎ 因为函数f(x)是定义在R上的奇函数，‎ 所以函数f(x)是R上的增函数，‎ 所以,‎ 所以.‎ 故答案为 ‎【点睛】本题主要考查函数的奇偶性的判定，考查函数的单调性的判定，考查函数的奇偶性和单调性的运用，意在考查学生对这些知识的掌握水平和分析推理能力.‎ ‎24.已知函数 在区间[1，2]上是单调函数，则实数的取值范围是_________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 对函数进行求导，导函数在区间[1，2]上恒非正或恒非负进行求解即可.‎ ‎【详解】，由题意可知：或在区间[1，2]上恒成立.‎ 当在区间[1，2]上恒成立时，，‎ 当时，，因此有；‎ 当在区间[1，2]上恒成立时，，‎ 当时，，因此有，‎ 综上所述：实数的取值范围是.‎ 故答案为：‎ ‎【点睛】本题考查了已知函数在区间上的单调性求参数取值范围，考查了导数的应用，考查了数学运算能力.‎ ‎25.设过曲线（为自然对数的底数）上任意一点处的切线为，总有过曲线上一点处的切线，使得，则实数的取值范围为___________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 求出的导函数的取值范围，然后根据题意，结合互相垂直的两直线的斜率关系，利用集合之间的关系，求出实数的取值范围.‎ ‎【详解】，设切线的斜率为，则有，因此由，‎ ‎，设切线的斜率为，则有，‎ 因为，所以，因为曲线上任意一点处的切线为，总有过曲线上一点处的切线，使得，所以有：‎ ‎.‎ 故答案为：‎ ‎【点睛】本题考查了利用导数的几何意义求切线的斜率问题，考查了存在性的理解，考查了两直线互相垂直斜率之间的关系，考查了数学运算能力.‎ 三、解答题（共25分）‎ ‎26.已知函数为自然对数的底数．‎ ‎（1）若曲线在点处的切线与轴平行，求的值；‎ ‎（2）若函数在内存在两个极值点，求的取值范围.‎ ‎【答案】(1) (2)‎ ‎【解析】‎ ‎【分析】‎ ‎（Ⅰ），由题设知，求得的值；‎ ‎（Ⅱ）若函数在内存在两个极值点，则方程 在内由两个不等实根,可列不等式组 ‎,即可求a的范围 ‎【详解】解：（Ⅰ），由题设知，故 ‎（Ⅱ）由题知，在内由两个不等实根，‎ ‎ .‎ ‎【点睛】本题考查了函数在一点处导数的几何意义，导数在极值中的应用,利用极值求参数的范围.‎ ‎27.已知函数.‎ ‎（1）求函数的单调区间；‎ ‎（2）当时，函数在上的最小值为，若不等式有解，求实数的取值范围．‎ ‎【答案】（1）答案见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）求出导函数，然后根据的符号进行分类讨论，并借助解不等式组的方法得到单调区间；（2）根据（1）中的结论求出当时，函数在上的最小值，因此问题转化为有解，即有解，构造函数，求出函数的最小值即可得到所求．‎ ‎【详解】（1）由，‎ 得，‎ ‎①当时，‎ 令，得，‎ 所以，或，即或，‎ 解得或．‎ 令，得，‎ 所以或，即或，‎ 解得或．‎ 所以函数的单调递增区间为，；单调递减区间为．‎ ‎②当时，‎ 令，得，由①可知；‎ 令，得，由①可知或．‎ 所以函数的单调递增区间为；单调递减区间为，．‎ 综上可得，‎ 当时，的单调递增区间为，；单调递减区间为．‎ 当时，的单调递增区间为；单调递减区间为，．‎ ‎（2）由（1）可知若，则当时，函数在上单调递减，在上单调递增，‎ 所以，‎ 所以不等式有解等价于有解，‎ 即有解，‎ 设，则，‎ 所以当时，，单调递减，‎ 当时，，单调递增，‎ 所以的极小值也是最小值，且最小值为，‎ 从而，‎ 所以实数的取值范围为．‎ ‎【点睛】（1）求函数的单调区间时，若函数解析式中含有字母、并且字母对结果产生影响时，需要对字母进行分类讨论，讨论时要选择合适的标准，同时分类时要做到不重不漏．‎ ‎（2）解答不等式有解的问题时，常用的方法是分离参数后转化为求函数的最值的问题，解题时要用到以下结论：在上有解；在上有解 ‎．若函数的最值不存在，则可利用函数值域的端点值来代替．‎