2017年高考数学（理科,江苏专版）二轮专题复习与策略（教师用书） 第1部分 专题4 第13讲 空间几何体

2017年高考数学（理科,江苏专版）二轮专题复习与策略（教师用书） 第1部分 专题4 第13讲 空间几何体

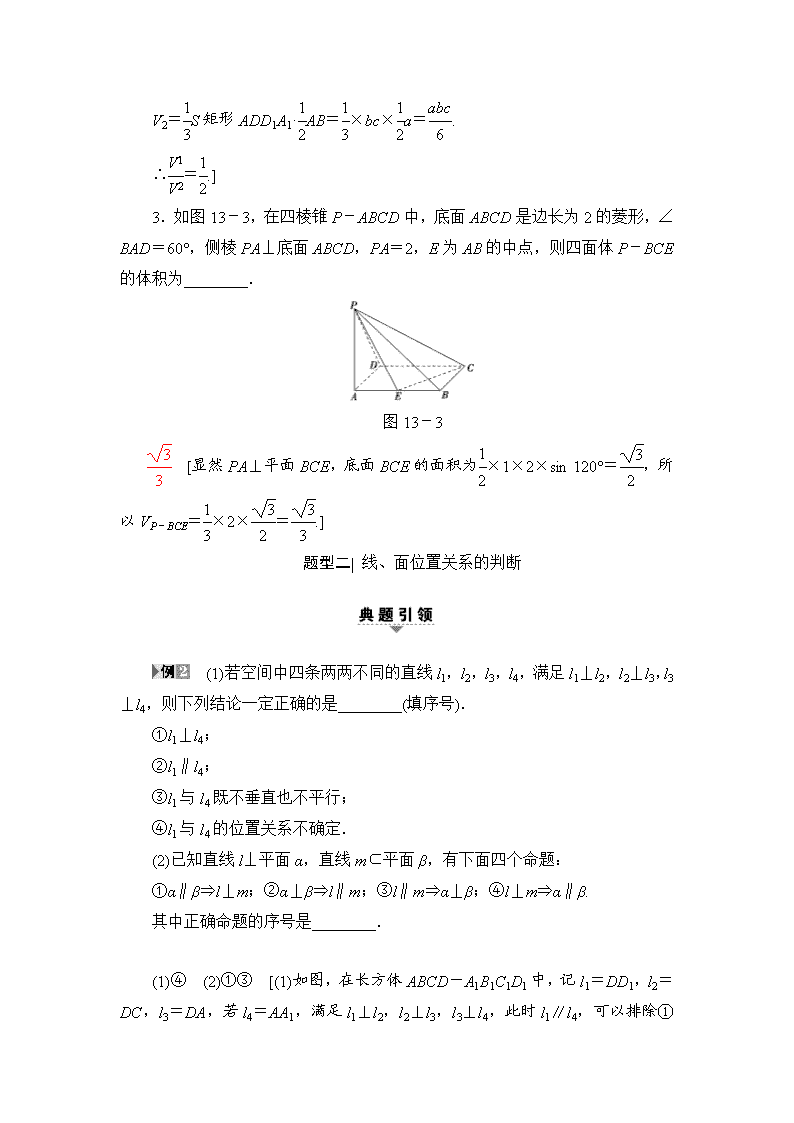
专题4　立体几何 第13讲　空间几何体 题型一| 空间几何体的表面积与体积 ‎　(1)(2014·江苏高考)设甲、乙两个圆柱的底面积分别为S1，S2，体积分别为V1，V2.若它们的侧面积相等，且＝，则的值是________．‎ ‎(2)(2016·南京盐城二模)如图13－1，正三棱柱ABC－A1B1C1中，AB＝4，AA1＝6.若E，F分别是棱BB1，CC1上的点，则三棱锥A－A1EF的体积是________．‎ 图13－1‎ ‎(1)　(2)8　[(1)设两个圆柱的底面半径和高分别为r1，r2和h1，h2，由＝，得＝，则＝.由圆柱的侧面积相等，得2πr1h1＝2πr2h2，即r1h1＝r2h2，则＝，所以＝＝，‎ ‎(2)极限法，取E，F分别与B1，C1重合，则 S三棱锥A－A1EF＝S△A1B1C1·AA1＝×AB2sin 60°·AA1‎ ‎＝×16××6＝8.]‎ ‎【名师点评】　求几何体的表面积及体积问题，可以多角度、多方位地考虑，熟记公式是关键所在．求三棱锥的体积，等体积转化是常用的方法，转换原则是其高易求，底面放在已知几何体的某一面上．‎ ‎1．已知一个圆锥的底面圆的半径为1，体积为π，则该圆锥的侧面积为________．‎ ‎【导学号：19592040】‎ ‎3π　[设圆锥的母线长为l，高为h，‎ 则由V＝πr2·h，‎ 得h＝＝＝2.‎ ‎∴母线l＝＝3，故圆锥的侧面积为S＝(2πr)l＝πrl＝π×1×3＝3π.]‎ ‎2．(2016·泰州期末)如图13－2，长方体ABCD－A1B1C1D1中，O为BD1的中点，三棱锥O－ABD的体积为V1，四棱锥O－ADD1A1的体积为V2，则的值为________．‎ 图13－2‎ 　[设AB＝a，AD＝b，A1A＝c，则 V1＝S△ABD·A1A＝×ab×c＝.‎ V2＝S矩形ADD1A1·AB＝×bc×a＝.‎ ‎∴＝.]‎ ‎3．如图13－3，在四棱锥P－ABCD中，底面ABCD是边长为2的菱形，∠BAD＝60°，侧棱PA⊥底面ABCD，PA＝2，E为AB的中点，则四面体P－BCE的体积为________．‎ 图13－3‎ 　[显然PA⊥平面BCE，底面BCE的面积为×1×2×sin 120°＝，所以VP－BCE＝×2×＝.]‎ 题型二| 线、面位置关系的判断 ‎　(1)若空间中四条两两不同的直线l1，l2，l3，l4，满足l1⊥l2，l2⊥l3，l3⊥l4，则下列结论一定正确的是________(填序号)．‎ ‎①l1⊥l4；‎ ‎②l1∥l4；‎ ‎③l1与l4既不垂直也不平行；‎ ‎④l1与l4的位置关系不确定．‎ ‎(2)已知直线l⊥平面α，直线m⊂平面β，有下面四个命题：‎ ‎①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β.‎ 其中正确命题的序号是________．‎ ‎(1)④　(2)①③　[(1)如图，在长方体ABCD－A1B1C1D1中，记l1＝DD1，l2＝DC，l3＝DA，若l4＝AA1，满足l1⊥l2，l2⊥l3，l3⊥l4，此时l1∥l4，可以排除①和③.若l4＝DC1，也满足条件，可以排除②，故填④.‎ ‎(2)直线l⊥平面α，α∥β⇒l⊥β⇒l⊥m，①对；α⊥β，l⊥α时，直线l与平面β可能平行，也可能在β内，直线l与直线m关系不确定，②错；l∥m，l⊥α⇒m⊥α⇒α⊥β，③对；由l⊥m，不能得出l⊥β，故也不能有α∥β，④错．]‎ ‎【名师点评】　空间线面位置关系的判断方法 ‎1．公理法：借助空间线面位置关系的判定定理和性质定理逐项判断来解决问题；‎ ‎2．模型法：借助空间几何模型，如在长方体、四面体等模型中观察线面位置关系，结合有关定理作出选择．‎ ‎1．给出下列命题：‎ ‎①若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；‎ ‎②若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；‎ ‎③若两条平行直线中的一条垂直于直线m，那么另一条直线也与直线m垂直；‎ ‎④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．‎ 其中，所有真命题的序号为________．‎ ‎①③④　[根据定理和一些常用结论知①③④正确．‎ ‎②中没有强调两条直线一定相交，否则就不一定平行．]‎ ‎2．已知m，n表示两条不同直线，α表示平面．下列说法正确的是________(填序号)．‎ ‎【导学号：19592041】‎ ‎①若m∥α，n∥α，则m∥n；‎ ‎②若m⊥α，n⊂α，则m⊥n；‎ ‎③若m⊥α，m⊥n，则n∥α；‎ ‎④若m∥α，m⊥n，则n⊥α.‎ ‎②　[若m∥α，n∥α，则m，n可能平行、相交或异面，①错；‎ 若m⊥α，n⊂α，则m⊥n，因为直线与平面垂直时，它垂直于平面内任一直线，②正确；‎ 若m⊥α，m⊥n，则n∥α或n⊂α，③错；‎ 若m∥α，m⊥n，则n与α可能相交，可能平行，也可能n⊂α，④错．]‎ 题型三| 多面体与球 ‎　(1)如图13－4，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为________cm3.‎ 图13－4‎ ‎(2)已知直三棱柱ABC－A1B1C1的6个顶点都在球O的球面上．若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为________．‎ ‎(1)　(2)　[(1)如图，作出球的一个截面，则MC＝8－6＝2(cm)，BM＝AB＝×8＝4(cm)．设球的半径为R cm，则R2＝OM2＋MB2＝(R－2)2＋42，‎ 所以R＝5，‎ 所以V球＝π×53＝π(cm3)．‎ ‎(2)因为直三棱柱中AB＝3，AC＝4，AA1＝12，AB⊥AC，所以BC＝5，且BC为过底面ABC的截面圆的直径．取BC中点D，则OD⊥底面ABC，则O在侧面BCC1B1内，矩形BCC1B1的对角线长即为球直径，所以2R＝＝13，即R＝.]‎ ‎【名师点评】　多面体与球切、接问题的求解策略 ‎1．涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解；‎ ‎2．若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，得4R2＝a2＋b2＋c2求解．‎ 已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一个球面上，则该球的体积为________．‎ 　[正四棱柱的外接球的球心为上下底面的中心连线的中点，所以球的半径r＝＝1，球的体积V＝r3＝.]‎