数学卷·2018届江西省南昌实验中学高二上学期期中数学试卷 （解析版）

数学卷·2018届江西省南昌实验中学高二上学期期中数学试卷 （解析版）

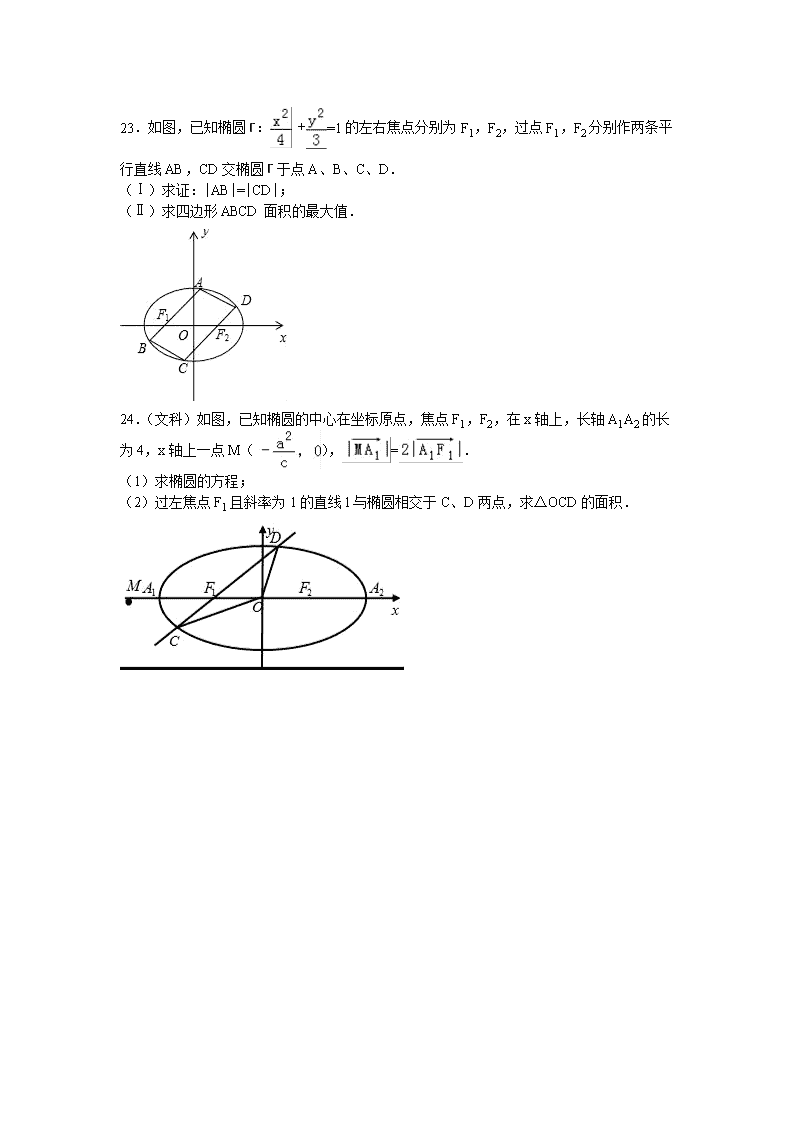
‎2016-2017学年江西省南昌实验中学高二（上）期中数学试卷 ‎　‎ 一、选择题（本大题共13小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的代号用2B铅笔填涂在答卷的相应表格内）‎ ‎1．抛物线y2=4x的焦点坐标为（　　）‎ A．（0，1） B．（1，0） C．（0，2） D．（2，0）‎ ‎2．双曲线﹣=1的渐近线方程是（　　）‎ A．y=±x B．y=±x C．y=±x D．y=±x ‎3．直线2x﹣3y﹣4=0的截距式方程为（　　）‎ A．﹣=1 B． +=1 C．﹣=1 D． +=1‎ ‎4．过圆x2+y2=25上一点P（3，4）的切线方程为（　　）‎ A．3x+4y+25=0 B．3x﹣4y+25=0 C．3x+4y﹣25=0 D．3x﹣4y﹣25=0‎ ‎5．椭圆+=1上一点P到一个焦点的距离为1，那么它到另一个焦点的距离为（　　）‎ A．2 B．3 C．4 D．5‎ ‎6．过点A（5，2），且在坐标轴上截距的绝对值相同的直线l的方程为（　　）‎ A．x﹣y﹣3=0‎ B．2x﹣5y=0‎ C．x﹣y﹣3=0或2x﹣5y=0‎ D．x﹣y﹣3=0或2x﹣5y=0或x+y﹣7=0‎ ‎7．过两直线3x+y﹣1=0与x+2y﹣7=0的交点，且与第二条直线垂直的直线方程为（　　）‎ A．2x﹣y+6=0 B．2x+y﹣6=0 C．x﹣3y+13=0 D．x﹣3y+7=0‎ ‎8．如果实数x，y满足（x﹣2）2+y2=3，那么的取值范围为（　　）‎ A．（﹣） B．[﹣] C．[] D．（﹣）‎ ‎9．圆x2+y2﹣2x﹣4y﹣20=0过点（1，﹣1）的最大弦长为m，最小弦长为n，则m+n=（　　）‎ A．17 B．18 C．19 D．20‎ ‎10．直线l与抛物线y2=4x相交于A，B两点，且线段AB的中点为（1，1），则l的方程为（　　）‎ A．2x﹣y﹣1=0 B．2x+y﹣3=0 C．x﹣2y+1=0 D．x+2y﹣3=0‎ ‎11．F1，F2为双曲线的两个焦点，以F2为圆心作圆，已知圆F2经过双曲线的中心，且与双曲线相交于M点，若直线MF1恰与圆F2相切，则该双曲线的离心率e为（　　）‎ A． +1 B． +2 C． +2 D． +1‎ ‎12．已知双曲线Γ：﹣=1（a＞0，b＞0）的上焦点F（0，c）（c＞0），M是双曲线下支上的一点，线段MF与圆x2+y2﹣y+=0相切于点D，且|MF|=3|DF|，则双曲线Γ的渐近线方程为（　　）‎ A．4x±y=0 B．x±4y=0 C．2x±y=0 D．x±2y=0‎ ‎13．椭圆4x2+y2=2上的点到直线2x﹣y﹣8=0 的距离的最小值为（　　）‎ A． B． C．3 D．6‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分，请将正确答案填空在答卷上）‎ ‎14．已知A（1，﹣4），B（﹣5，4），则以AB为直径的圆的标准方程是　　．‎ ‎15．已知函数f（x）=，且a＞b＞c＞0，则，，的大小关系为　　．‎ ‎16．已知双曲线mx2+5y2=5m的离心率e=2，则m=　　．‎ ‎17．已知椭圆+=1，P（1，1）为椭圆内一点，F1为椭圆的左焦点，M为椭圆上一动点：‎ ‎（理）则|MP|+|MF1|的最小值为　　；‎ ‎（文）则|MP|+|MF1|的取值范围为　　．‎ ‎　‎ 三、解答题（本大题共7小题，共70分，解答应写出文字说明、证明过程或演算步骤）‎ ‎18．求过点M（1，1），且圆心与已知圆C：x2+y2+2x+4y﹣11=0相同的圆的方程．‎ ‎19．已知圆C的方程为x2+y2=9‎ ‎（1）求过点P（2，﹣）的圆的切线方程；‎ ‎（2）求过点Q（3，5）的圆的切线方程．‎ ‎20．（1）已知双曲线的渐近线为3x+4y=0且经过点（8，3），求双曲线的方程；‎ ‎（2）若（1）中的双曲线被点A（8，3）平分的弦为MN，求MN所在的直线方程．‎ ‎21．已知动点P与平面上两定点连线的斜率的积为定值﹣．‎ ‎（1）试求动点P的轨迹方程C；‎ ‎（2）设直线l：y=kx+1与曲线C交于M．N两点，当|MN|=时，求直线l的方程．‎ ‎22．某隧道横断面由抛物线和矩形的三边组成，尺寸如图所示，某卡车载一集装箱，箱宽3m，车与箱共高4m，此车能否通过此隧道？请说明理由．‎ ‎23．如图，已知椭圆Г： +=1的左右焦点分别为F1，F2，过点F1，F2分别作两条平行直线AB，CD交椭圆Г于点A、B、C、D．‎ ‎（Ⅰ）求证：|AB|=|CD|；‎ ‎（Ⅱ）求四边形ABCD面积的最大值．‎ ‎24．（文科）如图，已知椭圆的中心在坐标原点，焦点F1，F2，在x轴上，长轴A1A2的长为4，x轴上一点M（），=．‎ ‎（1）求椭圆的方程；‎ ‎（2）过左焦点F1且斜率为1的直线l与椭圆相交于C、D两点，求△OCD的面积．‎ ‎　‎ ‎2016-2017学年江西省南昌实验中学高二（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共13小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的代号用2B铅笔填涂在答卷的相应表格内）‎ ‎1．抛物线y2=4x的焦点坐标为（　　）‎ A．（0，1） B．（1，0） C．（0，2） D．（2，0）‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】确定抛物线的焦点位置，进而可确定抛物线的焦点坐标．‎ ‎【解答】解：抛物线y2=4x的焦点在x轴上，且p=2‎ ‎∴=1‎ ‎∴抛物线y2=4x的焦点坐标为（1，0）‎ 故选B．‎ ‎　‎ ‎2．双曲线﹣=1的渐近线方程是（　　）‎ A．y=±x B．y=±x C．y=±x D．y=±x ‎【考点】双曲线的简单性质．‎ ‎【分析】渐近线方程是﹣=0，整理后就得到双曲线的渐近线方程．‎ ‎【解答】解：∵双曲线标准方程为﹣=1，‎ 其渐近线方程是﹣=0，‎ 整理得．‎ 故选：A．‎ ‎　‎ ‎3．直线2x﹣3y﹣4=0的截距式方程为（　　）‎ A．﹣=1 B． +=1 C．﹣=1 D． +=1‎ ‎【考点】直线的截距式方程．‎ ‎【分析】由令x=0，得y=﹣，令y=0，可得x=2，从而得到答案．‎ ‎【解答】解：令x=0，得y=﹣，‎ 令y=0，可得x=2，‎ ‎∴直线2x﹣3y﹣4=0的截距式方程为=1．‎ 故选D．‎ ‎　‎ ‎4．过圆x2+y2=25上一点P（3，4）的切线方程为（　　）‎ A．3x+4y+25=0 B．3x﹣4y+25=0 C．3x+4y﹣25=0 D．3x﹣4y﹣25=0‎ ‎【考点】圆的切线方程．‎ ‎【分析】由圆的方程找出圆心坐标和圆的半径，然后求出P与圆心的距离判断出P在圆上即P为切点，根据圆的切线垂直于过切点的直径，由圆心和M的坐标求出OP确定直线方程的斜率，根据两直线垂直时斜率乘积为﹣1，求出切线的斜率，根据P坐标和求出的斜率写出切线方程即可．‎ ‎【解答】解：由圆x2+y2=25，得到圆心A的坐标为（0，0），圆的半径r=5，‎ 而|AP|=5=r，所以P在圆上，则过P作圆的切线与AP所在的直线垂直，‎ 又P（3，4），得到AP所在直线的斜率为，所以切线的斜率为﹣，‎ 则切线方程为：y﹣4=﹣（x﹣3）即3x+4y﹣25=0．‎ 故选C．‎ ‎　‎ ‎5．椭圆+=1上一点P到一个焦点的距离为1，那么它到另一个焦点的距离为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】直接利用椭圆的定义求解即可．‎ ‎【解答】解：由椭圆+=1，‎ 得a=3，2a=6，‎ 由椭圆的定义可知：椭圆上一点P到椭圆的一个焦点的距离为1，则P到另一个焦点的距离为：5．‎ 故选：D．‎ ‎　‎ ‎6．过点A（5，2），且在坐标轴上截距的绝对值相同的直线l的方程为（　　）‎ A．x﹣y﹣3=0‎ B．2x﹣5y=0‎ C．x﹣y﹣3=0或2x﹣5y=0‎ D．x﹣y﹣3=0或2x﹣5y=0或x+y﹣7=0‎ ‎【考点】直线的截距式方程．‎ ‎【分析】当直线经过原点时，斜率为，可得要求的直线方程；‎ 当直线不经过原点时，设要求的直线方程为x±y=k，再把点（﹣4，﹣3）代入求得k的值，可得要求的直线方程，综合可得结论．‎ ‎【解答】解：当直线经过原点时，斜率为=，‎ 要求的直线方程为y=x，即．‎ 当直线不经过原点时，设要求的直线方程为x±y=k，‎ 再把点（5，2）代入可得5+2=k，或5﹣2=k，‎ 求得k=7，或k=3，故要求的直线方程为x+y﹣7=0，或x﹣y﹣3=0．‎ 综上可得，要求的直线方程为2x﹣5y=0或x+y﹣7=0，或x﹣y﹣3=0，‎ 故选：D．‎ ‎　‎ ‎7．过两直线3x+y﹣1=0与x+2y﹣7=0的交点，且与第二条直线垂直的直线方程为（　　）‎ A．2x﹣y+6=0 B．2x+y﹣6=0 C．x﹣3y+13=0 D．x﹣3y+7=0‎ ‎【考点】直线的一般式方程与直线的垂直关系．‎ ‎【分析】联立已知的两条直线方程求出交点的坐标，设与x+2y﹣7=0垂直的直线方程为2x﹣y+c=0，代入求出c，即可得到直线方程．‎ ‎【解答】解：联立已知的两直线方程得：，解得：，‎ 所以两直线的交点坐标为（﹣1，4），‎ 设与x+2y﹣7=0垂直的直线方程为2x﹣y+c=0，可得﹣2﹣4+c=0，∴c=6，‎ ‎∴所求直线方程为2x﹣y+6=0．‎ 故选A．‎ ‎　‎ ‎8．如果实数x，y满足（x﹣2）2+y2=3，那么的取值范围为（　　）‎ A．（﹣） B．[﹣] C．[] D．（﹣）‎ ‎【考点】直线与圆的位置关系；圆的标准方程．‎ ‎【分析】设过原点的圆的切线方程为y=kx，再根据圆心（2，0）到切线的距离等于半径，求得k的值，可得的取值范围．‎ ‎【解答】解：由题意可得，表示圆（x﹣2）2+y2=3上的点（x，y）与原点（0，0）连线的斜率，‎ 设为k，故此圆的切线方程为y=kx，‎ 再根据圆心（2，0）到切线的距离等于半径，可得r==，‎ 平方得k2=3，‎ 求得k=±，故的取值范围是[﹣]，‎ 故选C．‎ ‎　‎ ‎9．圆x2+y2﹣2x﹣4y﹣20=0过点（1，﹣1）的最大弦长为m，最小弦长为n，则m+n=（　　）‎ A．17 B．18 C．19 D．20‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】过点（1，﹣1）的最大弦长为直径，最短的弦为过（1，﹣1）与直径垂直的弦，根据两点间的距离公式求出弦心距，结合半径根据勾股定理可得．‎ ‎【解答】解：圆x2+y2﹣2x﹣4y﹣20=0，可化为圆（x﹣1）2+（y﹣2）2=25，‎ 圆的圆心（1，2），过点（1，﹣1）的最大弦长为直径，所以m=10；‎ 根据两点间的距离公式求出弦心距：2﹣（﹣1）=3，所以最小弦长为n=2=8，‎ 所以m+n=10+8=18，‎ 故选：B．‎ ‎　‎ ‎10．直线l与抛物线y2=4x相交于A，B两点，且线段AB的中点为（1，1），则l的方程为（　　）‎ A．2x﹣y﹣1=0 B．2x+y﹣3=0 C．x﹣2y+1=0 D．x+2y﹣3=0‎ ‎【考点】直线与抛物线的位置关系．‎ ‎【分析】设点作差，利用线段AB的中点坐标，即可求出直线l的斜率．然后求解直线方程．‎ ‎【解答】解：设A（x1，y 1），B（x2，y 2），‎ ‎∵A，B在曲线上，∴y12=4x1，y22=4x2，‎ 两式相减可得（y1+y2）（y1﹣y2）=4（x1﹣x2），‎ ‎∵线段AB的中点M（ 1，1），‎ ‎∴2（y1﹣y2）=4（x1﹣x2），‎ ‎∴=2．‎ 则l的方程为：y﹣1=2（x﹣1），即2x﹣y﹣1=0‎ 故选：A．‎ ‎　‎ ‎11．F1，F2为双曲线的两个焦点，以F2为圆心作圆，已知圆F2经过双曲线的中心，且与双曲线相交于M点，若直线MF1恰与圆F2相切，则该双曲线的离心率e为（　　）‎ A． +1 B． +2 C． +2 D． +1‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】分析知∠F1MF2是直角，又由MF2的长度为半径c，在直角三角形F1MF2中勾股定理建立相应的方程变形求e．‎ ‎【解答】解：易知圆F2的半径为c，又直线MF1恰与圆F2相切，∠F1MF2是直角，‎ ‎∵|F1F2|=2c，|MF2|=c，|F1M|=2a+c，‎ ‎∴在直角三角形F1MF2中有 ‎（2a+c）2+c2=4c2，‎ 即e2+2e﹣2=0，‎ ‎∵e＞1，∴e=+1．‎ 选选D．‎ ‎　‎ ‎12．已知双曲线Γ：﹣=1（a＞0，b＞0）的上焦点F（0，c）（c＞0），M是双曲线下支上的一点，线段MF与圆x2+y2﹣y+=0相切于点D，且|MF|=3|DF|，则双曲线Γ的渐近线方程为（　　）‎ A．4x±y=0 B．x±4y=0 C．2x±y=0 D．x±2y=0‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】由圆的方程求出圆心坐标，设出D的坐标，由题意列式求出D的坐标，结|MF|=3|DF|，求得M的坐标，再把M的坐标代入双曲线方程求得答案．‎ ‎【解答】解：由x2+y2﹣y+=0，得x2+（y﹣）2=，‎ 则该圆的圆心坐标为（0，），半径为．‎ 设切点D（x0，y0）（y0＞0），‎ 则由x2+y2﹣y+=0与（x0，y0﹣c）•（x0，y0﹣）=0，‎ 解得：x0=，y0=．‎ ‎∴D（，），‎ 由|MF|=3|DF|，得=3，得M（，﹣），‎ 代入 双曲线Γ：﹣=1（a＞0，b＞0）整理得b=2a，∴双曲线Г的渐近线方程为y=±x．‎ 故选：D．‎ ‎　‎ ‎13．椭圆4x2+y2=2上的点到直线2x﹣y﹣8=0 的距离的最小值为（　　）‎ A． B． C．3 D．6‎ ‎【考点】直线与椭圆的位置关系．‎ ‎【分析】设P（ cosθ， sinθ），0≤θ＜2π，求出P到直线2x﹣y﹣8=0 的距离d，由此能求出点P到直线的距离的最小值．‎ ‎【解答】解：∵椭圆4x2+y2=2，P为椭圆上一点，‎ ‎∴设P（ cosθ， sinθ），0≤θ＜2π，‎ ‎∴P到直线2x﹣y﹣8=0 的距离：‎ d==≤，‎ 当且仅当cos（）=1时取得最小值．‎ ‎∴点P到直线2x﹣y﹣8=0的距离的最小值为dmin=．‎ 故选：A．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，共20分，请将正确答案填空在答卷上）‎ ‎14．已知A（1，﹣4），B（﹣5，4），则以AB为直径的圆的标准方程是　（x+2）2+y2=25　．‎ ‎【考点】圆的标准方程．‎ ‎【分析】因为线段AB为所求圆的直径，所以利用中点坐标公式求出线段AB的中点即为所求圆的圆心坐标，再利用两点间的距离公式求出圆心C与点A之间的距离即为所求圆的半径，根据求出的圆心坐标与半径写出圆的标准方程即可．‎ ‎【解答】解：∵A（1，﹣4），B（﹣5，4），设圆心为C，‎ ‎∴圆心C的坐标为C（﹣2，0）；‎ ‎∴|AC|=5，即圆的半径r=5，‎ 则以线段AB为直径的圆的方程是（x+2）2+y2=25．‎ 故答案为：（x+2）2+y2=25．‎ ‎　‎ ‎15．已知函数f（x）=，且a＞b＞c＞0，则，，的大小关系为　　．‎ ‎【考点】指数函数的单调性与特殊点．‎ ‎【分析】由题意可以转化为f（x）上的点与原点连线的斜率，由此利用数形结合思想即可比较 ‎【解答】解：由题意可以转化为f（x）上的点与原点连线的斜率，‎ 根据函数f（x）=，‎ 设A（a，f（a）），B（b，f（b）），C（c，f（c）），‎ 观察图象知kOA＜kOB＜kOC，‎ ‎∴，‎ 故答案为：．‎ ‎　‎ ‎16．已知双曲线mx2+5y2=5m的离心率e=2，则m=　﹣15　．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】由双曲线mx2+5y2=5m，化为标准方程，利用离心率e=2，即可求出m的值，‎ ‎【解答】解：双曲线mx2+5y2=5m即：，‎ ‎∴e2=1=4，∴m=﹣15．‎ 故答案为：﹣15．‎ ‎　‎ ‎17．已知椭圆+=1，P（1，1）为椭圆内一点，F1为椭圆的左焦点，M为椭圆上一动点：‎ ‎（理）则|MP|+|MF1|的最小值为　　；‎ ‎（文）则|MP|+|MF1|的取值范围为　（6﹣，6+）　．‎ ‎【考点】椭圆的简单性质；直线与椭圆的位置关系．‎ ‎【分析】（理）由椭圆的第二定义，得d=，从而|MP|+|MF1|=|MA|+|MP|，当M、P、A三点共线时，|MP|+|MF1|取最小值，由此能求出结果．‎ ‎（文）由椭圆定义得|PF1|=2a﹣|PF2|=6﹣|PF2|，由||PA|﹣|PF2||≤|AF2|，由此能求出||MP|+|MF1|的取值范围．‎ ‎【解答】解：（理）由椭圆的第二定义，得： =e，‎ ‎∴d=，‎ 由椭圆的方程+=1，得e=，‎ 右准线方程为：x=，‎ ‎|MP|+|MF1|=|MA|+|MP|，‎ ‎∴当M、P、A三点共线时，‎ ‎|MP|+|MF1|取最小值，最小值为：1+=．‎ 故答案为：．‎ ‎（文）∵椭圆+=1，‎ ‎∴a=3，b=，c=2，F1（﹣2，0），F2（2，0），‎ 由椭圆定义得|PF1|=2a﹣|PF2|=6﹣|PF2|，‎ 由||PA|﹣|PF2||≤|AF2|==，‎ 知，‎ ‎∴||MP|+|MF1|的取值范围为．‎ 故答案为：（6﹣，6+）．‎ ‎　‎ 三、解答题（本大题共7小题，共70分，解答应写出文字说明、证明过程或演算步骤）‎ ‎18．求过点M（1，1），且圆心与已知圆C：x2+y2+2x+4y﹣11=0相同的圆的方程．‎ ‎【考点】圆的一般方程．‎ ‎【分析】根据圆心C（﹣1，﹣2），要求的圆的半径MC 的值，可得要求的圆的方程．‎ ‎【解答】解：圆C：x2+y2+2x+4y﹣11=0的圆心C（﹣1，﹣2），‎ 要求的圆的半径为MC==，‎ 故要求的圆的方程为（x+1）2+（y+2）2=13．‎ ‎　‎ ‎19．已知圆C的方程为x2+y2=9‎ ‎（1）求过点P（2，﹣）的圆的切线方程；‎ ‎（2）求过点Q（3，5）的圆的切线方程．‎ ‎【考点】圆的切线方程．‎ ‎【分析】（1）P在圆上，过点P（2，﹣）的圆的切线方程为2x﹣y=9，可得结论；‎ ‎（2）分类讨论，利用圆心到直线的距离等于半径，即可得出结论．‎ ‎【解答】解：（1）P在圆上，过点P（2，﹣）的圆的切线方程为2x﹣y=9，‎ 即；‎ ‎（2）斜率不存在时，显然满足题意，‎ 斜率存在时，设直线方程为y﹣5=k（x﹣3），即kx﹣y﹣3k+5=0‎ 圆心到直线的距离d==3，∴k=，‎ ‎∴切线方程为8x﹣15y+51=0．‎ 综上所述，过点Q（3，5）的圆的切线方程为x=3或8x﹣15y+51=0‎ ‎　‎ ‎20．（1）已知双曲线的渐近线为3x+4y=0且经过点（8，3），求双曲线的方程；‎ ‎（2）若（1）中的双曲线被点A（8，3）平分的弦为MN，求MN所在的直线方程．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】（1）由题意可知：设双曲线方程为9x2﹣16y2=λ，将点（8，3）代入，即可求得λ的值，即可求得双曲线的方程；‎ ‎（2）设直线MN的方程为y﹣3=k（x﹣8），代入双曲线方程，由韦达定理可知x1+x2=，由中点坐标公式可知： =8，即可求得k的值，即可求得直线MN的方程．‎ ‎【解答】解：（1）渐近线方程为3x+4y=0，‎ 设双曲线方程为9x2﹣16y2=λ，‎ 将（8，3）代入9x2﹣16y2=λ，解得：λ=144，‎ 双曲线的方程；；‎ ‎（2）由题意可知：设直线MN的方程为y﹣3=k（x﹣8），M（x1，y1），N（x2，y2），‎ ‎∴，整理得：（9﹣16k2）x2﹣32k（3﹣8k）x﹣16（3﹣8k）2=144，‎ 由韦达定理可知：x1+x2=，‎ 弦为MN的中点A（8，3），‎ 由中点坐标公式可知： =8，‎ 则=16，解得：k=，‎ ‎∴MN所在的直线方程3x﹣2y﹣18=0．‎ ‎　‎ ‎21．已知动点P与平面上两定点连线的斜率的积为定值﹣．‎ ‎（1）试求动点P的轨迹方程C；‎ ‎（2）设直线l：y=kx+1与曲线C交于M．N两点，当|MN|=时，求直线l的方程．‎ ‎【考点】直线与圆锥曲线的综合问题；圆锥曲线的轨迹问题．‎ ‎【分析】（Ⅰ）设出P的坐标，利用动点P与平面上两定点连线的斜率的积为定值，建立方程，化简可求动点P的轨迹方程C．‎ ‎（Ⅱ）直线l：y=kx+1与曲线C方程联立，利用韦达定理计算弦长，即可求得结论．‎ ‎【解答】解：（Ⅰ）设动点P的坐标是（x，y），由题意得：kPAkPB=‎ ‎∴，化简，整理得 故P点的轨迹方程是，（x≠±）‎ ‎（Ⅱ）设直线l与曲线C的交点M（x1，y1），N（x2，y2），‎ 由得，（1+2k2）x2+4kx=0‎ ‎∴x1+x2=，x1 x2=0，‎ ‎|MN|=，‎ 整理得，k4+k2﹣2=0，解得k2=1，或k2=﹣2（舍）‎ ‎∴k=±1，经检验符合题意．‎ ‎∴直线l的方程是y=±x+1，即：x﹣y+1=0或x+y﹣1=0‎ ‎　‎ ‎22．某隧道横断面由抛物线和矩形的三边组成，尺寸如图所示，某卡车载一集装箱，箱宽3m，车与箱共高4m，此车能否通过此隧道？请说明理由．‎ ‎【考点】抛物线的应用．‎ ‎【分析】取抛物线顶点为原点，水平向右为x轴正方向建立直角坐标系，设抛物线方程，把x=3代入抛物线方程求得y，取抛物线与矩形的结合点代入抛物线方程求得p，抛物线方程可求取x=求得y，进而与隧道的高度进行比较，结果发现而者的差大于车与箱的高，判断出卡车可以通过此隧道．‎ ‎【解答】解：取抛物线顶点为原点，水平向右为x轴正方向建立直角坐标系，设抛物线方程为x2=﹣2py（p＞0），‎ 当x=3时，y=﹣3，即取抛物线与矩形的结合点（3，﹣3），‎ 代入x2=﹣2py，得9=6p，则，故抛物线方程为x2=﹣3y．‎ 已知集装箱的宽为3m，取，则．‎ 而隧道高为5m， =．‎ 所以，卡车可以通过此隧道．‎ ‎　‎ ‎23．如图，已知椭圆Г： +=1的左右焦点分别为F1，F2，过点F1，F2分别作两条平行直线AB，CD交椭圆Г于点A、B、C、D．‎ ‎（Ⅰ）求证：|AB|=|CD|；‎ ‎（Ⅱ）求四边形ABCD面积的最大值．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（I）设AB方程为x=my﹣1，则CD方程为x=my+1，分别与椭圆方程联立得出A，B，C，D坐标的关系，利用弦长公式即可得出|AB|=|CD|；‎ ‎（II）求出S△AOB的面积的最大值，即可得出四边形ABCD面积的最大值．‎ ‎【解答】解：（I）F1（﹣1，0），F2（1，0），‎ 设A（x1，y1），B（x2，y2），直线AB的方程为x=my﹣1．‎ 联立方程组，消元得（3m2+4）y2﹣6my﹣9=0，‎ ‎∴y1+y2=，y1y2=﹣．‎ 设C（x3，y3），D（x4，y4），直线CD的方程为x=my+1．‎ 联立方程组，消元得（3m2+4）y2+6my﹣9=0．‎ ‎∴y3+y4=﹣，y3y4=﹣．‎ ‎∴y1+y2=﹣（y3+y4），y1y2=y3y4，‎ ‎∴|y1﹣y2|=|y3﹣y4|，‎ ‎∵|AB|=|y1﹣y2|，|CD|=|y3﹣y4|，‎ ‎∴|AB|=|CD|．‎ ‎（II）∵四边形ABCD是平行四边形，‎ ‎∴S▱ABCD=4S△AOB，‎ 又S△AOB=|OF1||y1﹣y2|===6=6．‎ 设m2+1=t，f（t）=9t+，则t≥1，f′（t）=9﹣＞0，‎ ‎∴f（t）在[1，+∞）上为增函数，∴f（t）≥f（1）=10．‎ ‎∴S△AOB≤6=，‎ ‎∴四边形ABCD面积的最大值为4×=6．‎ ‎　‎ ‎24．（文科）如图，已知椭圆的中心在坐标原点，焦点F1，F2，在x轴上，长轴A1A2的长为4，x轴上一点M（），=．‎ ‎（1）求椭圆的方程；‎ ‎（2）过左焦点F1且斜率为1的直线l与椭圆相交于C、D两点，求△OCD的面积．‎ ‎【考点】直线与圆锥曲线的关系；椭圆的标准方程．‎ ‎【分析】（1）利用长轴A1A2的长为4，x轴上一点M（），=，建立方程组，求出a，b，即可求椭圆的方程；‎ ‎（2）把直线l的方程代入椭圆的方程化简，利用根与系数的关系，求出|y1﹣y2|的值，即可求△OCD的面积．‎ ‎【解答】解：（1）设椭圆方程为+=1（a＞b＞0），则||=﹣a，||=a﹣c，‎ 由题意，∴a=2，b=，c=1，‎ ‎∴椭圆方程为=1；‎ ‎（2）由题意，直线l的方程为x﹣y+1=0，设C（x1，y1 ），D（x2，y2），‎ 直线方程代入椭圆方程整理得7y2﹣6y﹣9=0，‎ ‎∴y1+y2=，y1y2=﹣，‎ ‎∴|y1﹣y2|==，‎ ‎∴S△OCD==．‎