2020届二轮复习 随机事件的概率 课件（35张）（全国通用）

2020届二轮复习 随机事件的概率 课件（35张）（全国通用）

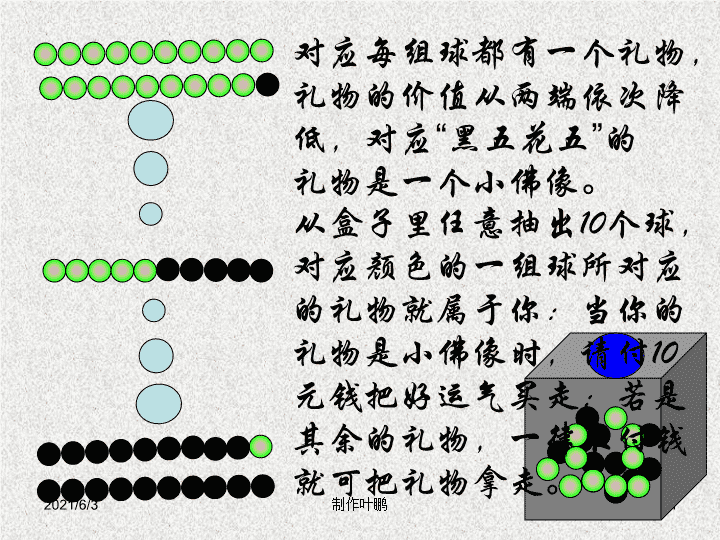
2021/1/13 制作叶鹏 1 对应每组球都有一个礼物，礼物的价值从两端依次降低，对应“黑五花五”的礼物是一个小佛像。 从盒子里任意抽出 10 个球，对应颜色的一组球所对应的礼物就属于你：当你的礼物是小佛像时，请付 10 元钱把好运气买走；若是其余的礼物，一律不付钱就可把礼物拿走。 2021/1/13 制作叶鹏 2 随机事件 的 概率 二中 叶鹏 2021/1/13 制作叶鹏 3 1 、试验探究 2021/1/13 制作叶鹏 4 1 、试验探究 从盒中一次摸一个球，猜一猜，会摸到什么颜色的球？ 一定是白球！ 2021/1/13 制作叶鹏 5 木柴燃烧 , 产生热量 明天，地球还会转动 问题情境 在一定条件下，事先就 能断定发生或不发生 某种结果，这种现象就是 确定性现象 . 实心铁块丢入水中 , 铁块浮起 一天内，在常温下，石头会被风化掉 2021/1/13 制作叶鹏 6 1 、试验探究 再放入 9 个黄球 现在从盒中一次摸一个球，猜一猜，会摸出什么颜色的球？ 不能预先确定摸出的是什么颜色的球 ! 2021/1/13 制作叶鹏 7 转盘转动后，指针指向有色区域 在一定条件下，某种现象 可能发生也可能不发生 ，事先 不能断定 出现哪种结果，这种现象就是 随机现象 . 这两人各买 1 张彩票，她们中奖了 问题情境 2021/1/13 制作叶鹏 8 对于某个现象，如果能让其条件实现一次，就是进行了一次 试验 . 而试验的每一种可能的结果，都是 一个 事件 . 事件的表示 : 以后我们用 A 、 B 、 C 等大写字母表示 随机事件 ，简称 事件 . 2021/1/13 制作叶鹏 9 2. 发现问题 （ 1 ） 必然事件： 在一定条件下必然要发生的事情。 （ 2 ） 不可能事件： 在一定条件下不可能发生的事情。 （ 3 ） 随机事件： 在一定条件下可能发生也可能不发生的事情。 2021/1/13 制作叶鹏 10 例 1 、下列哪些是随机事件，哪些是必然事件，哪些是不可能事件？ （ 1 ）“抛一石块，下落” 是必然事件 2021/1/13 制作叶鹏 11 （ 2 ）在标准大气压下 且温度低于 0℃ 时，冰融化 是不可能事件 2021/1/13 制作叶鹏 12 (3) 某人射击一次 中靶！ 是随机事件 2021/1/13 制作叶鹏 13 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (4) 如果 a ＞ b, 那么 a － b ＞ 0 是必然事件 2021/1/13 制作叶鹏 14 (5) 掷一枚硬币，出现正面 是随机事件 2021/1/13 制作叶鹏 15 (6) 导体通电后，发热 是必然事件 2021/1/13 制作叶鹏 16 得到 4 号签 5 4 3 1 2 3 4 1 2 是随机事件 (7) 从分别标有号数 1 ， 2 ， 3 ， 4 ， 5 的 5 张标签中任取一张 2021/1/13 制作叶鹏 17 (8) 某电话机在 1 分钟内收到 2 次呼叫 是随机事件 2021/1/13 制作叶鹏 18 (9) 没有水份，种子能发芽 是不可能事件 2021/1/13 制作叶鹏 19 (10) 在常温下，焊锡熔化 是不可能事件 2021/1/13 制作叶鹏 20 3 、提出问题： 随机事件在一次试验中是否发生虽然不能事先确定，但在大量重复试验的情况下，它的发生是否会呈现出一定的规律性呢？ 2021/1/13 制作叶鹏 21 我扔一块硬币，要是能出现正面就好了。 在抛掷硬币若干次 的试验中，出现正面的 次数占总次数的百分比 为多少呢？即出现正面 的频率为多少？ 2021/1/13 制作叶鹏 22 事件：投掷一枚硬币，出现正面。 2021/1/13 制作叶鹏 23 抛掷次数 ( n ) 正面向上次数 ( 频数 m ) 历史上曾有人作过抛掷硬币的大量重复试验，请同学们来看这样一组数据： （附表一：抛掷硬币试验结果表） 频率 : 2048 1061 0.5158 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 30000 14984 0.4996 72088 36142 0.5011 出现正面的频率值都接近于 0.5 2021/1/13 制作叶鹏 24 每批粒数 n 2 5 10 70 130 310 700 1500 2000 3000 发芽粒数 m 2 4 9 60 116 282 639 1339 1806 2715 1 0.8 0.9 0.857 0.892 0.910 0.913 0.893 0.903 0.905 抽取球数 n 50 100 200 500 1000 2000 优等品数 m 45 92 194 470 954 1902 0.9 0.92 0.97 0.94 0.954 0.951 附表二：某批乒乓球产品质量检验表 优等品频率 附表三：某种油菜籽在相同条件下的发芽试验结果表 发芽频率 优等品的频率接近于 0.95 油菜籽发芽的频率接近于 0.9 2021/1/13 制作叶鹏 25 随机事件在一次试验中是否发生虽然不能事先确定，但随着试验次数的不断增加，它的发生会呈现出一定的规律性，正如我们刚才看到的：某事件发生的频率在大量重复的试验中总是接近于某个常数。 2021/1/13 制作叶鹏 26 4 、概念形成 （ 1 ）： 随即事件的概率：一般地，在大量重复进行同一试验时，事件 A 发生的频率总是接近于某个常数，在它附近摆动，这时就把这个常数叫做事件 A 的概率，记作 P ( A ) 。 2021/1/13 制作叶鹏 27 几点说明： 1 求一个事件的概率的基本方法是通过大量的重复试验； 2 只有当频率在某个常数附近摆 动时， 这个常数才叫做事件 的概率 ； 3 必然事件的概率为 1 ，不可能事 件的概率为 0 。因此 0≦P(A)≦1 2021/1/13 制作叶鹏 28 频率具有随机性 它反映某一随机事件出现的频繁程度 , 即随机事件出现的可能性 . 它反映了随机事件的属性 . 4 “ 频率”和“概率”两个概念区分 : 若事件的概率未知 , 常用频率作为它的估计值 . 概率是一个客观常数 2021/1/13 制作叶鹏 29 （ 2 ）随机现象的两个特征 结果的随机性： 即在相同的条件下做重复的试验时 , 如果试验的结果不止一个 , 则在试验前无法预料哪一种结果将发生。 频率的稳定性： 即大量重复试验时 , 任意结果 ( 事件 ) 出现的频率尽管是随机的 , 却“稳定”在某一个常数附近 , 试验的次数越多 , 频率与这一常数的偏差大的可能性越小 . 这一常数就成为该事件的概率。 2021/1/13 制作叶鹏 30 5 应用举例 例 2 ：对某电视机厂生产的电视机进行抽样检测的数 据如下： 抽取台数 50 100 200 300 500 1000 优等品数 40 92 192 285 478 954 （ 1 ）计算表中优等品的各个频率； （ 2 ）该厂生产的电视机优等品的概率是多少？ 解（ 1 ）各次优等品的概率为 　 0.8 ， 0.92 ， 0.96 ， 0.95 ， 0.956 ， 0.954 　（ 2 ）优等品的概率是 0.95 。 2021/1/13 制作叶鹏 31 例 3 ． （ 1 ）某厂一批产品的次品率为 1/10 ，问任意抽取其中 10 件产品是否一定会发现一件次品？为什么？ （ 2 ） 10 件产品中次品率为 1/10 ，问这 10 件产品中必有一件次品的说法是否正确？为什么？ 错误 正确 2021/1/13 制作叶鹏 32 回顾小结 随机事件及其概率 事件的含义 事件的分类 事件的表示 频率与概率 2021/1/13 制作叶鹏 33 8 、作业布置 （ 1 ）课本 P126 1 、 2 、 3 （ 2 ）思考题： 不做大量重复的试验，就下列事件直接分析 它的概率： 掷一枚均匀硬币，出现 “ 正面朝上 ” 的概率是多少？ 掷一枚骰子，出现 “ 正面是 3 ” 的概率是多少？出现 “ 正面是 3 的倍数 ” 的概率是多少？出现 “ 正面是奇数 ” 的概率是多少？ 本班 55 名学生，其中女生 20 人，现任选一人，则被选中的是男生的概率是多少？被选中的是女生的概率是多少？ （ 3 ）、预习： 课本 P127 ~ P130. 预习提纲： ①何为基本事件，等可能性事件？ ②如何求等可能性事件的概率？ 2021/1/13 制作叶鹏 34 2006.4. 谢谢指导 2021/1/13 制作叶鹏 35 事件： （蒲丰投针试验）将一根长为 l 的针，任意投在一组距离为 2l 的平行线间，它与平行线相交。