高考数学复习课时提能演练(十三) 2_10

高考数学复习课时提能演练(十三) 2_10

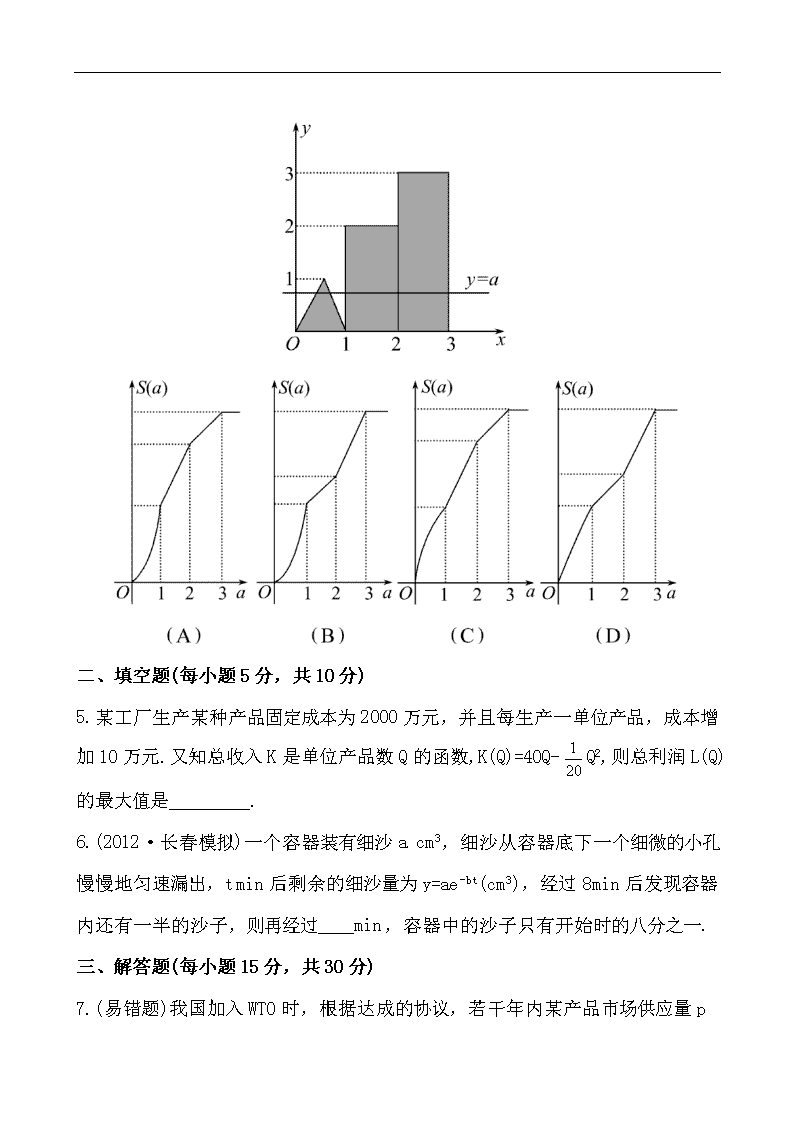
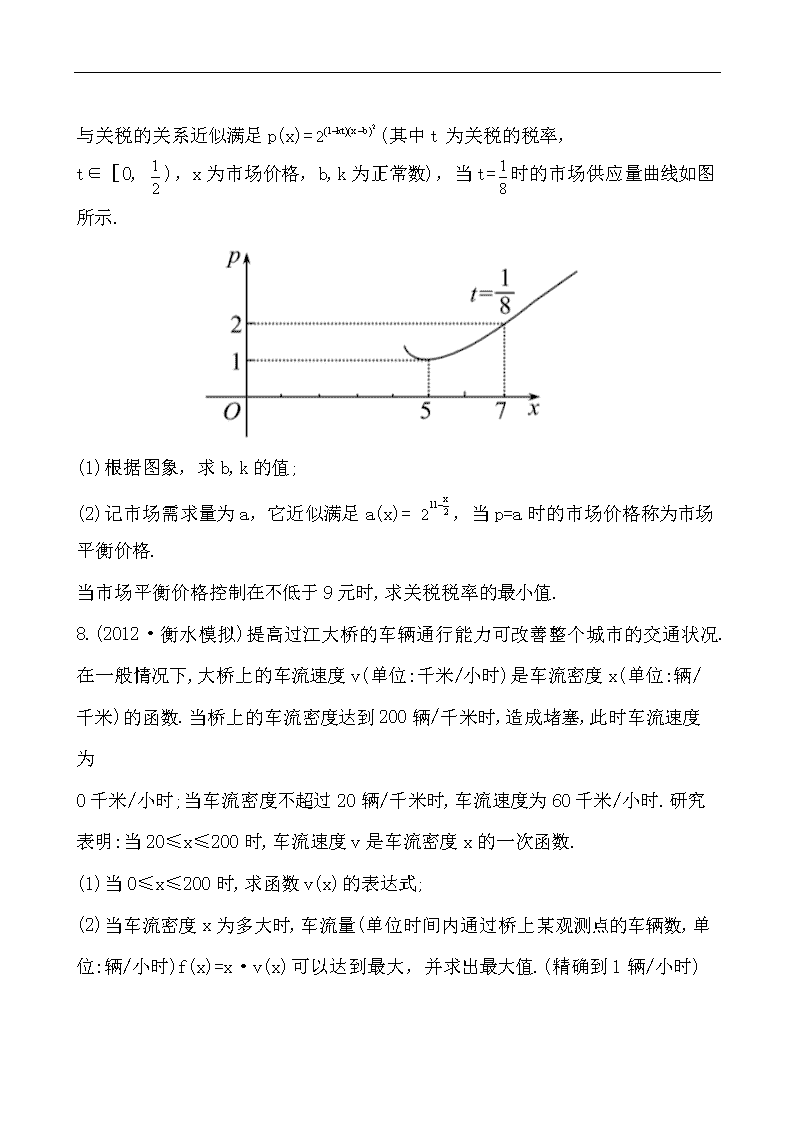
‎ ‎ 课时提能演练(十三)‎ ‎(40分钟 60分)‎ 一、选择题(每小题5分，共20分)‎ ‎1.某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y=5x+4 000，而手套出厂价格为每副10元，则该厂为了不亏本，日产手套至少为( )‎ ‎(A)200副 (B)400副 ‎(C)600副 (D)800副 ‎2.（2012·三明模拟）某化工厂生产一种溶液，按市场要求，杂质含量不能超过0.1%，若最初生产出的溶液含杂质2%，需要进行过滤，且每过滤一次可使杂质含量减少，则要使产品达到市场要求至少应过滤（ ）‎ ‎(A)3次 (B)4次 (C)5次 (D)6次 ‎3.某地区植被被破坏，土地沙化越来越严重，最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是( )‎ ‎(A)y=0.2x (B)y=‎ ‎(C)y= (D)y=0.2+log16x ‎4.（2012·福州模拟）图中的阴影部分由底为1，高为1的等腰三角形及高为2和3的两矩形所构成.设函数S=S(a)(a≥0)是图中阴影部分介于平行线y=0及y=a之间的那一部分的面积，则函数S(a)的图象大致为（ ）‎ 二、填空题(每小题5分，共10分)‎ ‎5.某工厂生产某种产品固定成本为2 000万元，并且每生产一单位产品，成本增加10万元.又知总收入K是单位产品数Q的函数,K(Q)=40Q-Q2,则总利润L(Q)的最大值是_________.‎ ‎6.(2012·长春模拟)一个容器装有细沙a cm3，细沙从容器底下一个细微的小孔慢慢地匀速漏出，t min后剩余的细沙量为y=ae-bt(cm3)，经过8 min后发现容器内还有一半的沙子，则再经过____min，容器中的沙子只有开始时的八分之一.‎ 三、解答题(每小题15分，共30分)‎ ‎7.(易错题 ‎)我国加入WTO时，根据达成的协议，若干年内某产品市场供应量p与关税的关系近似满足p(x)=(其中t为关税的税率，‎ t∈［0, )，x为市场价格，b,k为正常数)，当t=时的市场供应量曲线如图所示.‎ ‎(1)根据图象，求b,k的值;‎ ‎(2)记市场需求量为a，它近似满足a(x)= ，当p=a时的市场价格称为市场平衡价格.‎ 当市场平衡价格控制在不低于9元时,求关税税率的最小值.‎ ‎8.(2012·衡水模拟)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为 ‎0千米/小时;当车流密度不超过20辆/千米时,车流速度为‎60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.‎ ‎(1)当0≤x≤200时,求函数v(x)的表达式;‎ ‎(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大，并求出最大值.(精确到1辆/小时)‎ 答案解析 ‎1.【解析】选D.利润z=10x-y=10x-(5x+4 000)≥0.解得x≥800.‎ ‎2.【解析】选C.设过滤x次后，杂质含量为y，则y=2%·()x,由y≤0.1%,解得x≥5.即至少要过滤5次.‎ ‎3. 【解析】选C.由已知数据逐个验证知C较接近.‎ ‎4. 【解析】选C.S（a）=,故选C.‎ ‎5.【解析】总利润L(Q)=40Q-Q2-10Q-2 000‎ ‎=-(Q-300)2+2 500.‎ 故当Q=300时,总利润最大值为2 500万元.‎ 答案：2 500万元 ‎6.【解析】当t=0时，y=a，‎ 当t=8时,y=ae-8b=a，∴e-8b=,‎ 容器中的沙子只有开始时的八分之一时,‎ 即y=ae-bt=a,‎ e-bt==(e-8b)3=e-24b,‎ 则t=24,所以再经过16 min.‎ 答案：16‎ ‎7.【解析】(1)由图象,知 即 由≠0，解得b=5,k=6.‎ ‎(2)p=a时,有 即(1-6t)(x-5)2=11-,‎ ‎2(1-6t)= .‎ 由x≥9,得x-5≥4,即0＜≤.‎ 令m=，则2(1-6t)=‎17m2‎-m(m∈(0, ］).‎ 由二次函数的性质得 当m=时,2(1-6t)max=,‎ 则1-6t≤,t≥.‎ 所以关税税率的最小值为.‎ ‎8.【解析】(1)由题意:当0≤x≤20时,v(x)=60;‎ 当20≤x≤200时,设v(x)=ax+b.‎ 由已知得方程组解得 故函数v(x)的表达式为 v(x)= ‎ ‎(2)依题意并由(1)可得 f(x)= ‎ 当0≤x≤20时,f(x)为增函数，故当x=20时,其最大值为60×20=1 200;‎ 当20＜x≤200时,f(x)=x(200-x)≤.‎ 当且仅当x=200-x，即x=100时,等号成立.‎ 所以，当x=100时,f(x)在区间(20,200］上取得最大值.‎ 综上,当x=100时,f(x)在区间［0,200］上取得最大值f(x)max=≈3 333.‎ 即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3 333辆/小时.‎