2019届二轮复习立体几何学案（全国通用）

2019届二轮复习立体几何学案（全国通用）

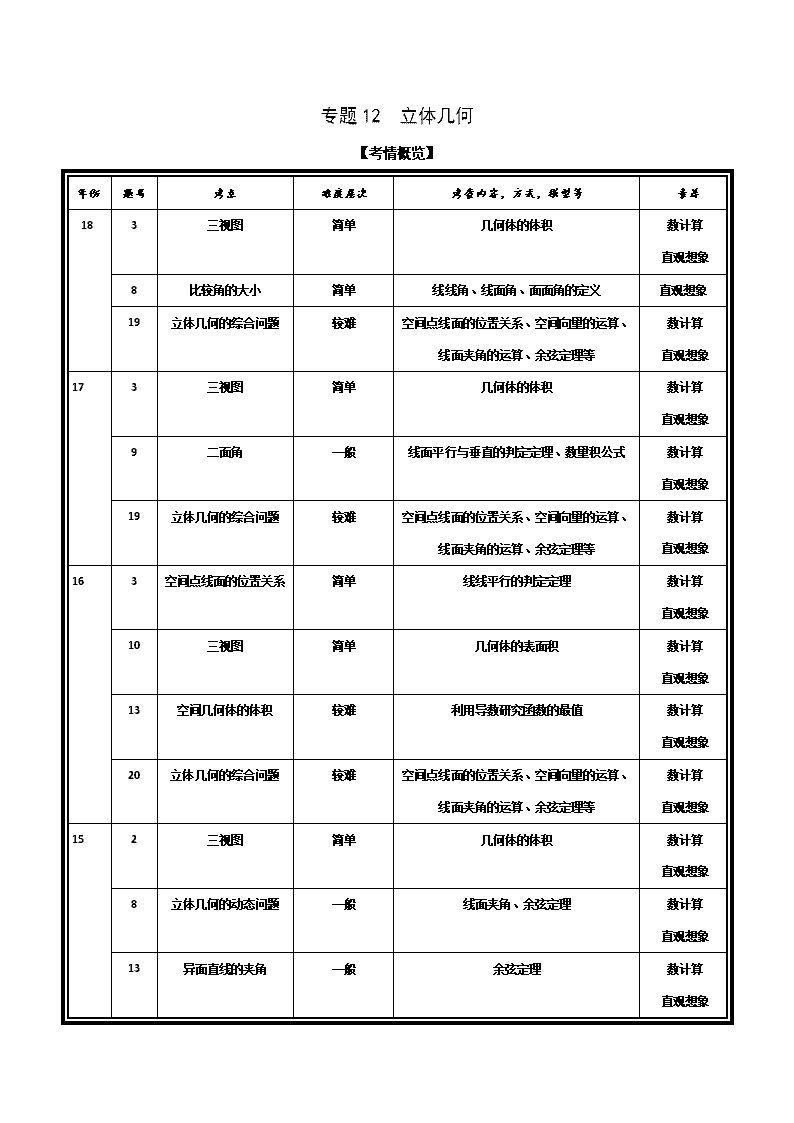
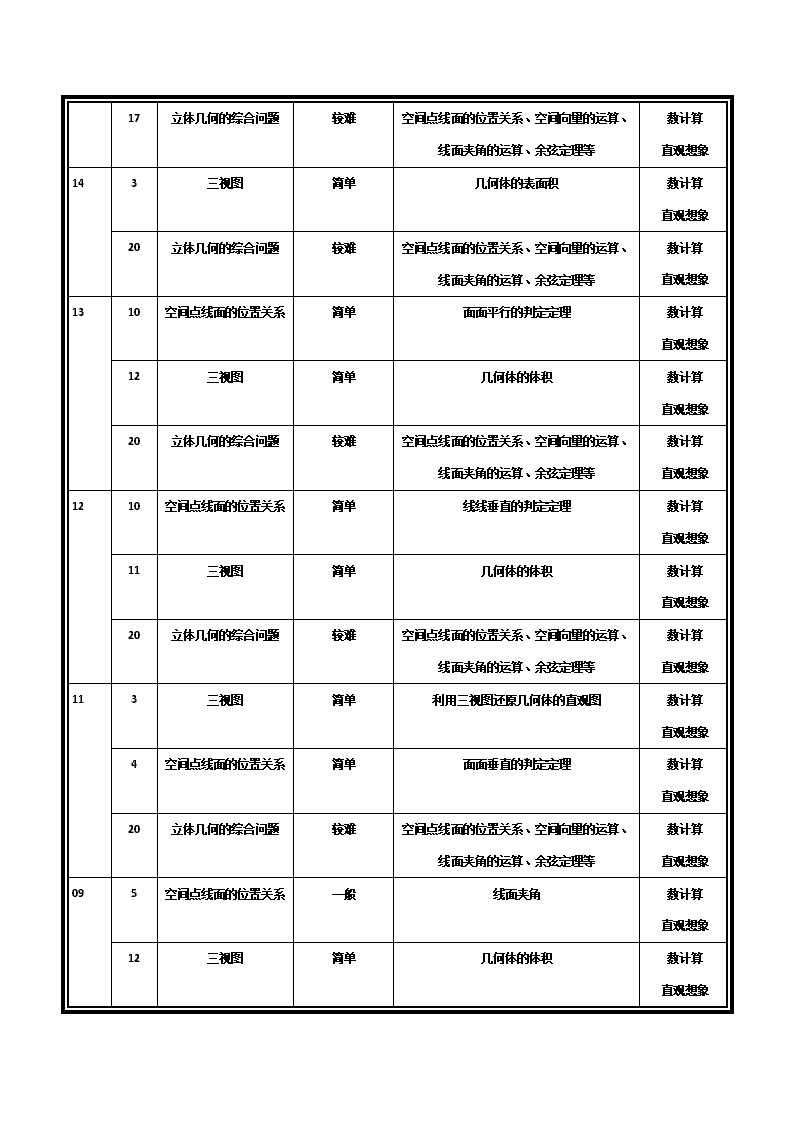
【考情概览】 年份 题号 考点 难度层次 考查内容，方式，模型等 素养 3 三视图 简单 几何体的体积 数计算 直观想象 8 比较角的大小 简单 线线角、线面角、面面角的定义 直观想象 18 19 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 3 三视图 简单 几何体的体积 数计算 直观想象 9 二面角 一般 线面平行与垂直的判定定理、数量积公式 数计算 直观想象 17 19 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 3 空间点线面的位置关系 简单 线线平行的判定定理 数计算 直观想象 10 三视图 简单 几何体的表面积 数计算 直观想象 13 空间几何体的体积 较难 利用导数研究函数的最值 数计算 直观想象 16 20 立体几何的综合问题] 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 2 三视图 简单 几何体的体积 数计算 直观想象 8 立体几何的动态问题 一般 线面夹角、余弦定理 数计算 直观想象 15 13 异面直线的夹角 一般 余弦定理 数计算 直观想象 17 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 3 三视图 简单 几何体的表面积 数计算 直观想象 14 20 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 10 空间点线面的位置关系 简单 面面平行的判定定理 数计算 直观想象 12 三视图 简单 几何体的体积 数计算 直观想象 13 20 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 10 空间点线面的位置关系 简单 线线垂直的判定定理 数计算 直观想象 11 三视图 简单 几何体的体积 数计算 直观想象 12 20 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 3 三视图 简单 利用三视图还原几何体的直观图 数计算 直观想象 4 空间点线面的位置关系 简单 面面垂直的判定定理 数计算 直观想象 11 20 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 5 空间点线面的位置关系 一般 线面夹角 数计算 直观想象 09 12 三视图 简单 几何体的体积 数计算 直观想象 20 立体几何的综合问题 较难 空间点线面的位置关系、空间向量的运算、 线面夹角的运算、余弦定理等 数计算 直观想象 【应试策略】 1.如图所示，在长方体 OAEB－O1A1E1B1 中，|OA|＝3，|OB|＝4，|OO1|＝2，点 P 在棱 AA1 上，且|AP|＝ 2|PA1|，点 S 在棱 BB1 上，且|SB1|＝2|BS|，点 Q、R 分别是 O1B1、AE 的中点，求证：PQ∥RS. 【答案】PQ∥RS 【应试策略】 证明直线与平面平行，只须证明直线的方向向量与平面的法向量的数量积为零，或证直线的方向向量与平 面内的不共线的两个向量共面，然后说明直线在平面外即可．这样就把几何的证明问题转化为了数量的计 算问题． 2.如图所示，在棱长为 1 的正方体 OABC­O1A1B1C1 中，E，F 分别是棱 AB，BC 上的动点，且 AE＝BF＝x，其中 0≤x≤1，以 O 为原点建立空间直角坐标系 O­xy . ] (1)求证 A1F⊥C1E； (2)若 A1，E，F，C1 四点共面，求证：A1F→ ＝ 1 2A1C1→ ＋A1E→ . 【答案】（1）A1F⊥C1E；（2）A1F→ ＝ 1 2A1C1→ ＋A1E→ . 【应试策略】 1.证明直线与直线垂直，只需要证明两条直线的方向向量垂直，而直线与平面垂直，平面与平面垂直可转 化为直线与直线垂直证明． 2.要证明两线垂直，需转化为两线对应的向量垂直，进一步转化为证明两向量的数量积为零，这是证明两 线垂直的基本方法，线线垂直是证明线面垂直，面面垂直的基础． 3.证明线面垂直，可利用判定定理．如本题解法． 4.用向量证明两个平面垂直，关键是求出两个平面的法向量，把证明面面垂直转化为法向量垂直． 3.长方体 ABCD－A1B1C1D1 中，AB＝AA1＝2，AD＝1，E 为 CC1 的中点，则异面直线 BC1 与 AE 所成角的余弦值 为(　　) A. 10 10 　　　　　　　　 B. 30 10 C. 2 15 10 D. 3 10 10 【答案】 B 【应试策略】 1.求一对异面直线所成角：一是按定义平移转化为两相交直线的夹角；二是在异面直线上各取一向量，转 化为两向量的夹角或其补角，无论哪种求法，都应注意角的范围的限定． 2. 利用直线的方向向量的夹角求异面直线的夹角时，注意区别：当异面直线的方向向量的夹角为锐角或直 角时，就是此异面直线所成的角；当异面直线的方向向量的夹角为钝角时，其补角才是异面直线所成的 角． 【真题展示】 一、选择题 1.【2018 年，浙江卷 3】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（ ） A．2 B．4 C．6 D．8 【答案】C 【解答】该几何体的立体图形为四棱柱， . 2.【2018 年，浙江卷 8】已知四棱锥 S−ABCD 的底面是正方形，侧棱长均相等，E 是线段 AB 上的点（不含 端点），设 SE 与 BC 所成的角为 θ1，SE 与平面 ABCD 所成的角为 θ2，二面角 S−AB−C 的平面角为 θ3，则 （ ） A．θ1≤θ2≤θ3 B．θ3≤θ2≤θ1 C．θ1≤θ3≤θ2 D．θ2≤θ3≤θ1 【答案】D 3.【2017 年，浙江卷 3】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是 侧视图 俯视图 正视图 2 211 (1 2) 2 2 62V + ×= × = （第 3 题图） A． B． C． D． 【答案】A 【解析】试题分析：根据所给三视图可还原几何体为半个圆锥和半个棱锥拼接而成的组合体，所以，几何 体的体积为 ，选 A． 【考点】 三视图 【名师点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相 等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几 何体的宽；侧视图的高是几何体的高，宽是几何体的宽．由三视图画出直观图的步骤和思考方法：1、首先 看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高 度；3、画出整体，然后再根据三视图进行调整． 4.【2014 年.浙江卷.理 3】某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是 A. 90 B. 129 C. 132 D. 138 【答案】D 【解析】有三视图可知，此几何体如下图，故几何体的表面积为 ，故选 D． 12 π + 32 π + 3 12 π + 3 32 π + 21 1 13 ( 2 1) 13 2 2 2V π× π= × × + × × = + 2cm 2cm 2cm 2cm 12 4 6 2 3 4 3 6 3 3 3 4 3 5 2 3 4 1382S = × × + × × + × + × + × + × + × × × = 【考点】三视图,几何体的表面积. 5.【2012 年.浙江卷.理 10】已知矩形 ABCD，AB＝1， ．将△ABD 沿矩形的对角线 BD 所在的直 线进行翻折，在翻折过程中，(　　) A．存在某个位置，使得直线 AC 与直线 BD 垂直 B．存在某个位置，使得直线 AB 与直线 CD 垂直 C．存在某个位置，使得直线 AD 与直线 BC 垂直 D．对任意位置，三对直线“AC 与 BD”，“AB 与 CD”，“AD 与 BC”均不垂直 【答案】B 6.【2011 年.浙江卷.理 3】若某几何体的三视图如图所示，则这个几何体的直观图可以是 【答案】 D 【解析】A，B 与正视图不符，C 与俯视图不符，故选 D 7.【2011 年.浙江卷.理 4】下列命题中错误的是 （A）如果平面 ，那么平面 内一定存在直线平行于平面 （B）如果平面 不垂直于平面 ，那么平面 内一定不存在直线垂直于平面 （C）如果平面 ，平面 ， ，那么 （D）如果平面 ，那么平面 内所有直线都垂直于平面 【答案】 D 6 4 2 2 4 6 8 10 12 14 16 20 15 10 5 5 10 15 20 34 4 3 3 2BC = α β⊥ 平面 α β α β α β α γ⊥ 平面 β γ⊥ 平面 =lα β∩ l γ⊥ 平面 α β⊥ 平面 α β 【解析】两个平面垂直，两个平面上的所有直线都不是垂直了，比如 α 平面垂直 β 平面，垂线为 AB，直线 CD 属于 α，与 AB 交与 E 点，角度为 60°，不垂直平面 ，故选 D 8. 【2009 年.浙江卷.理 5】在三棱柱 中，各棱长相等，侧掕垂直于底面，点 是侧面 的中心，则 与平面 所成角的大小是 ( ) A． B． C． D． 【答案】C 9.【2015 高考浙江，理 2】某几何体的三视图如图所示（单位：cm），则该几何体的体积是（ ） A. B. C. D. 【答案】C. 【解析】试题分析：由题意得，该几何体为一立方体与四棱锥的组合，如下图所示，∴体积 ，故选 C. 【考点定位】1.三视图；2.空间几何体的体积计算. 10.【2016 高考浙江理数】已知互相垂直的平面 交于直线 l.若直线 m，n 满足 则（ ） A．m∥l B．m∥n C．n⊥l D．m⊥n 【答案】C 【解析】试题分析：由题意知 ， ．故选 C． β 1 1 1ABC A B C− D 1 1BB C C AD 1 1BB C C 30 45 60 90 38cm 312cm 332 3 cm 340 3 cm 3 32223 12 23 =××+=V α β， ,m nα β∥ ⊥ ， ,l lα β β= ∴ ⊂ ,n n lβ⊥ ∴ ⊥ 【考点】空间点、线、面的位置关系． 【思路点睛】解决这类空间点、线、面的位置关系问题，一般是借助长方体（或正方体），能形象直观地看 出空间点、线、面的位置关系． 11.【2013 年.浙江卷.理 10】在空间中，过点 A 作平面 π 的垂线，垂足为 B，记 B＝fπ(A)．设 α，β 是两个 不同的平面，对空间任意一点 P，Q1＝fβ[fα(P)]，Q2＝fα[fβ(P)]，恒有 PQ1＝PQ2，则(　　)． A．平面 α 与平面 β 垂直 B．平面 α 与平面 β 所成的(锐)二面角为 45° C．平面 α 与平面 β 平行 D．平面 α 与平面 β 所成的(锐)二面角为 60° 【答案】A 12.【2015 高考浙江，理 8】如图，已知 ， 是 的中点，沿直线 将 折成 ，所 成二面角 的平面角为 ，则（ ） A. B. C. D. ABC∆ D AB CD ACD∆ A CD′∆ A CD B′− − α A DB α′∠ ≤ A DB α′∠ ≥ A CB α′∠ ≤ A CB α′∠ ≤ 【答案】B. 【考点定位】立体几何中的动态问题 13.【2017 年，浙江卷 9】如图，已知正四面体 D–ABC（所有棱长均相等的三棱锥），P，Q，R 分别为 AB， BC，CA 上的点，AP=PB， ，分别记二面角 D–PR–Q，D–PQ–R，D–QR–P 的平面角为 α，β，γ， 则 （第 9 题图） A．γ<α<β B．α<γ<β C．α<β<γ D．β<γ<α 【答案】B 【考点】 空间角（二面角） 【名师点睛】立体几何是高中数中的重要内容，也是高考重点考查的考点与热点．这类问题的设置一般有 线面位置关系的证明与角度距离的计算等两类问题．解答第一类问题时一般要借助线面平行与垂直的判定 定理进行；解答第二类问题时先建立空间直角坐标系，运用空间向量的坐标形式及数量积公式进行求解． 14.【2014 年.浙江卷.文 6】设 、 是两条不同的直线， 、 是两个不同的平面，则（ ） A.若 ， ，则 B.若 ， ，则 C.若 ， ， ，则 D.若 ， ， ，则 【答案】C 【解析】 2BQ CR QC RA = = m n α β nm ⊥ α//n α⊥m β//m αβ ⊥ α⊥m β⊥m β⊥n α⊥n α⊥m nm ⊥ β⊥n αβ ⊥ α⊥m 【考点】空间中的线线、线面、面面的位置关系，容易题. 15.【2013 年.浙江卷.文 4】设 m，n 是两条不同的直线，α，β 是两个不同的平面(　　)． A．若 m∥α，n∥α，则 m∥n B．若 m∥α，m∥β，则 α∥β C．若 m∥n，m⊥α，则 n⊥α D．若 m∥α，α⊥β，则 m⊥β 【答案】C 【解析】A 选项中直线 m，n 可能平行，也可能相交或异面，直线 m，n 的关系是任意的；B 选项中，α与β 也可能相交，此时直线 m 平行于α，β的交线；D 选项中，m 也可能平行于β.故选 C 16.【2013 年.浙江卷.文 5】已知某几何体的三视图(单位：cm)如图所示，则该几何体的体积是(　　)． A．108 cm3 B．100 cm3 C．92 cm3 D．84 cm3 【答案】B 【解析】由三视图可知，该几何体是如图所示长方体去掉一个三棱锥，故几何体的体积是 6×3×6－ × ×3×42＝100(cm3)．故选 B. 1 3 1 2 17.【2012 年.浙江卷.文 3】已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积是(　　) A．1 cm3 B．2 cm3 C．3 cm3 D．6 cm3 【答案】A　 【解析】由三视图得，该三棱锥底面面积 S＝ ×2×1＝1(cm2)，高为 3 cm，由体积公式，得 V＝ Sh＝ ×1×3＝1(cm3)． 18.【2012 年.浙江卷.文 5】设 l 是直线，α，β 是两个不同的平面，(　　) A．若 l∥α，l∥β，则 α∥β B．若 l∥α，l⊥β，则 α⊥β C．若 α⊥β，l⊥α，则 l⊥β D．若 α⊥β，l∥α，则 l⊥β 【答案】B　 19.【2011 年.浙江卷.文 4】若直线 不平行于平面 ，且 ，则 (A) 内的所有直线与 异面 (B) 内不存在与 平行的直线 (C) 内存在唯一的直线与 平行 (D) 内的直线与 都相交 1 2 1 3 1 3 l a l a⊄ a l a l a l a l 【答案】 B 【解析】直线 不平行于平面 ， 所以 与 相交，故选 B 20.【2011 年.浙江卷.文 7】几何体的三视图如图所示，则这个几何体的直观图可以是 【答案】 B 【解析】A，C 与正视图不符，D 与俯视图不符，故选 B 21.【2010 年.浙江卷.文 8】若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是 （A） cm3 （B） cm3 （C） cm3 （D） cm3 【答案】B 22.【2009 年.浙江卷.文 4】设 是两个不同的平面， 是一条直线，以下命题正确的是（ ） A．若 ，则 B．若 ，则 C．若 ，则 D．若 ，则 【答案】C 【解析】对于 A、B、D 均可能出现 ，而对于 C 是正确的．w.w.w c 23.【2009 年.浙江卷.文 12】若某几何体的三视图（单位： ）如图所示，则此几何体的体积是 ． l a l a⊄ l a 352 3 320 3 224 3 160 3 ,α β l ,l α α β⊥ ⊥ l β⊂ / / , / /l α α β l β⊂ , / /l α α β⊥ l β⊥ / / ,l α α β⊥ l β⊥ //l β cm 3cm 【答案】 18 【解析】该几何体是由二个长方体组成，下面体积为 ，上面的长方体体积为 ，因此 其几何体的体积为 18 24.【2015 高考浙江，文 4】设 ， 是两个不同的平面， ， 是两条不同的直线，且 ， （ ） A．若 ，则 B．若 ，则 C．若 ，则 D．若 ，则 【答案】A 【考点定位】直线、平面的位置关系. 25.【2015 高考浙江，文 7】如图，斜线段 与平面 所成的角为 ， 为斜足，平面 上的动点 满 足 ，则点 的轨迹是（ ） A．直线 B．抛物线 C．椭圆 D．双曲线的一支 【答案】C 1 3 3 9× × = 3 3 1 9× × = α β l m l α⊂ m β⊂ l β⊥ α β⊥ α β⊥ l m⊥ //l β //α β //α β //l m ΑΒ α 60 Β α Ρ 30∠ΡΑΒ =  Ρ 【解析】由题可知，当 点运动时，在空间中，满足条件的 绕 旋转形成一个圆锥，用一个与圆锥高 成 角的平面截圆锥，所得图形为椭圆.故选 C. 【考点定位】1.圆锥曲线的定义；2.线面位置关系. 二、填空题 1.【2013 年.浙江卷.理 12】若某几何体的三视图(单位：cm)如图所示，则此几何体的体积等于 cm3. 【答案】24 【解析】由三视图可知该几何体为如图所示的三棱柱割掉了一个三棱锥． ＝ ×3×4×5－ × ×3×4×3＝30－6＝24. 2.【2012 年.浙江卷.理 11】已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积等于 cm3． 【答案】1 Ρ ΑΡ ΑΒ 60 1 1 1 1 1 1 1 1A EC ABC A B C ABC E A B CV V V− − −= − 1 2 1 3 1 2 【解析】由图可知三棱锥底面积 (cm2)，三棱锥的高 h＝2 cm，根据三棱锥体积公式， (cm3)． 3.【2009 年.浙江卷.理 12】若某几何体的三视图（单位： ）如图所示，则此几何体的体积是 ． 【答案】18 4.【2015 高考浙江，理 13】如图，三棱锥 中， ，点 分别是 的中点，则异面直线 ， 所成的角的余弦值是 ． 【答案】 . 【解析】试题分析：如下图，连结 ，取 中点 ，连结 ， ，则可知 即为异面直 线 ， 所成角（或其补角）易得 ， 1 31 32 2S = × × = 1 1 3 2 13 3 2V Sh= = × × = cm 3cm A BCD− 3, 2AB AC BD CD AD BC= = = = = = ,M N ,AD BC AN CM 8 7 DN DN P PM PC PMC∠ AN CM 22 1 == ANPM ， ， ∴ ，即异面直线 ， 所成角的余弦值为 . 【考点定位】异面直线的夹角. 5.【2016 高考浙江理数】某几何体的三视图如图所示（单位：cm），则该几何体的表面积是 cm2，体积 是 cm3. 【答案】 【考点】1、三视图；2、空间几何体的表面积与体积． 【方法点睛】解决由三视图求空间几何体的表面积与体积问题，一般是先根据三视图确定该几何体的结构 特征，再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积． 6.【2009 年.浙江卷.理 17】如图，在长方形 中， ， ， 为 的中点， 为线段 （端点除外）上一动点．现将 沿 折起，使平面 平面 ．在平面 内过点 作 ， 为垂足．设 ，则 的取值范围是 ． 31222 =+=+= CNPNPC 2222 =−= AMACCM 8 7 2222 328cos = ×× −+=∠PMC AN CM 8 7 72 32 ABCD 2AB = 1BC = E DC F EC AFD∆ AF ABD ⊥ ABC ABD D DK AB⊥ K AK t= t 【答案】 【解析】此题的破解可采用二个极端位置法，即对于 F 位于 DC 的中点时， ，随着 F 点到 C 点时，因 平 面 ， 即 有 ， 对 于 ， 又 ，因此有 ，则有 ，因此 的取值范围是 7.【2016 高考浙江理数】如图，在△ABC 中，AB=BC=2，∠ABC=120°.若平面 ABC 外的点 P 和线段 AC 上的 点 D，满足 PD=DA，PB=BA，则四面体 PBCD 的体积的最大值是 . 【答案】 1 ,12      1t = , ,CB AB CB DK CB⊥ ⊥ ∴ ⊥ ADB CB BD⊥ 2, 1, 3CD BC BD= = ∴ = 1, 2AD AB= = AD BD⊥ 1 2t = t 1 ,12      1 2 . 设 ，因为 ，所以 . 则 . （1）当 时，有 ， 故 . 此时， . ，因为 ， ] 所以 ，函数 在 上单调递减，故 . （2）当 时，有 ，故 . 此时， . E D C BA P 2 1 (2 3 ) 6 2 3 4 x x x x −= − + 2 22 3 4 ( 3) 1t x x x= − + = − + 0 2 3x≤ ≤ 1 2t≤ ≤ 2| 3 | 1x t− = − 0 3x≤ ≤ 2| 3 | 3 1x x t− = − = − 23 1x t= − − 2 21 ( 3 1)[2 3 ( 3 1)] 6 t tV t − − − − −= 21 4 1 4( )6 6 t tt t −= ⋅ = − 2 1 4( ) ( 1)6V t t ′ = − − 1 2t≤ ≤ ( ) 0V t′ < ( )V t [1,2] 1 4 1( ) (1) ( 1)6 1 2V t V≤ = − = 3 2 3x< ≤ 2| 3 | 3 1x x t− = − = − 23 1x t= + − 2 21 ( 3 1)[2 3 ( 3 1)] 6 t tV t + − − + −= 21 4 1 4( )6 6 t tt t −= ⋅ = − 由（1）可知，函数 在 单调递减，故 . 综上，四面体 的体积的最大值为 . 【考点】1、空间几何体的体积；2、用导数研究函数的最值． 【思路点睛】先根据已知条件求出四面体的体积，再对 的取值范围讨论，用导数研究函数的单调性，进 而可得四面体的体积的最大值． 8.【2016 高考浙江文数】某几何体的三视图如图所示（单位：cm），则该几何体的表面积是 cm2，体 积是 cm3. 【答案】80，40 【考点】三视图. 【方法点睛】解决由三视图求空间几何体的表面积与体积问题，一般是先根据三视图确定该几何体的结构 特征，再准确利用几何体的表面积与体积公式计算该几何体的表面积与体积． 三、解答题 1.【2018 年，浙江卷 19】（本题满分 15 分）如图，已知多面体 ABCA1B1C1，A1A，B1B，C1C 均垂直于平面 ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2． ( )V t (1,2] 1 4 1( ) (1) ( 1)6 1 2V t V< = − = PBCD 1 2 x （Ⅰ）证明：AB1⊥平面 A1B1C1； （Ⅱ）求直线 AC1 与平面 ABB1 所成的角的正弦值． 19.答案：（1）略；（2） 过点 作 的垂线段交 于点 . 39 13 1B 1A A 1A A H 则 ， ，∴ . 在 中， ， ∴ ，② 综合①②，∵ ， 平面 ， 平面 ， ∴ 平面 . （2）过点 作 的垂线段交 于点 ，以 为原点，以 所在直线为 轴，以 所在直线为 轴， 以 所在直线为 轴，建立空间直角坐标系 . 2.【2017 年，浙江卷 19】（本题满分 15 分）如图，已知四棱锥 P–ABCD，△PAD 是以 AD 为斜边的等腰直 角三角形， ，CD⊥AD，PC=AD=2DC=2CB，E 为 PD 的中点． 1 2B H AB= = 1 2A H = 1 1 2 2A B = 1 1A B A∆ 2 2 2 1 1 1 1AA AB A B= + 1 1 1AB A B⊥ 1 1 1 1 1A B B C B∩ = 1 1A B ⊂ 1 1 1A B C 1 1B C ⊂ 1 1 1A B C 1AB ⊥ 1 1 1A B C B AB AC I B AB x BI y 1B B z B xyz− / /BC AD （第 19 题图） （Ⅰ）证明： 平面 PAB； （Ⅱ）求直线 CE 与平面 PBC 所成角的正弦值． 【答案】（Ⅰ）见解析；（Ⅱ） ． 即四边形 BCEF 为平行四边形，所以 ， 因此 平面 PAB． （Ⅱ）分别取 BC，AD 的中点为 M，N．连接 PN 交 EF 于点 Q，连接 MQ． P A B C D E / /CE 2 8 / /CE BF / /CE 【考点】证明线面平行，求线面角 【名师点睛】本题主要考查线面平行的判定定理、线面垂直的判定定理及面面垂直的判定定理，属于中档 题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一 条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四 边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行 于另一平面．本题（1）是就是利用方法①证明的．另外，本题也可利用空间向量求解线面角． 3.【2015 高考浙江，理 17】如图，在三棱柱 -中， ， ， ， 在底面 的射影为 的中点， 为 的中点. （1）证明： D 平面 ； （2）求二面角 -BD- 的平面角的余弦值. 1 1 1ABC A B C− 90BAC∠ =  2AB AC= = 1 4A A = 1A ABC BC D 1 1B C 1A ⊥ 1A B C 1A 1B 【答案】（1）详见解析；（2） . 【考点定位】1.线面垂直的判定与性质；2.二面角的求解 4.【2014 年.浙江卷.理 20】（本题满分 15 分）如图，在四棱锥 中，平面 平面 . 1 8 − BCDEA− ⊥ABC ======∠=∠ ACBEDECDABBEDCDEBCDE ,1,2,90, 0 2 （1）证明： 平面 ; （2）求二面角 的大小 【答案】（Ⅰ）详见解析；（Ⅱ）二面角 的大小是 ． 【解析】 试题解析：（I）在直角梯形 中，由 ， 得， ，由 ，则 ，即 ，又平面 平面 ，从而 平面 ，所以 ，又 ，从而 平面 ； （II）方法一：作 ，与 交于点 ，过点 作 ，与 交于点 ，连结 ，由 6 4 2 2 4 6 8 10 12 14 16 18 20 15 10 5 5 10 15 20 E D C B A ⊥DE ACD EADB −− EADB −− 6 π BCDE 1DE BE= = 2CD = 2BD BC= = 2, 2AC AB= = 2 2 2AB AC BC= + AC BC⊥ ⊥ABC BCDE AC ⊥ BCDE AC DE⊥ DE DC⊥ DE ⊥ ACD BF AD⊥ AD F F FG DE AE G BG （I）知， ，则 所以 是二面角 的平面角，在直角梯形 中， 由 ，得 ，又平面 平面 ，得 平面 ，从而， ，由于 平面 ，得： ，在 中，由 ， ，得 ， 6 4 2 2 4 6 8 10 12 14 16 18 20 15 10 5 5 10 15 20 G F E D C B A DE AD⊥ FG AD⊥ BFG∠ EADB −− BCDE 2 2 2CD BD BC= + BD BC⊥ ⊥ABC BCDE BD ⊥ ABC BD AB⊥ AC ⊥ BCDE AC CD⊥ Rt ACD 2CD = 2AC = 6AD = 试题点评：本题主要考查空间点，线，面位置关系，二面角等基础知识，空间向量的应用 ，同时考查空间 想象能力，与推理论证，运算求解能力． 5.【2013 年.浙江卷.理 20】(本题满分 15 分)如图，在四面体 A－BCD 中，AD⊥平面 BCD，BC⊥CD，AD＝ 2，BD＝ .M 是 AD 的中点，P 是 BM 的中点，点 Q 在线段 AC 上，且 AQ＝3QC． (1)证明：PQ∥平面 BCD； (2)若二面角 C－BM－D 的大小为 60°，求∠BDC 的大小． 【答案】 【解析】 4 2 2 4 6 8 10 12 14 16 18 20 15 10 5 5 10 15 20 Z Y x E D C B A 2 2 由题意知 A(0， ，2)，B(0， ，0)，D(0， ，0)．设点 C 的坐标为(x0，y0,0)． 因为 ，所以 Q .因为 M 为 AD 的中点，故 M(0， ，1)． 又 P 为 BM 的中点，故 P ，所以 ＝ . 又平面 BCD 的一个法向量为 u＝(0,0,1)，故 ·u＝0.又 PQ 平面 BCD，所以 PQ∥平面 BCD． (2)解：设 m＝(x，y， )为平面 BMC 的一个法向量．由 ＝(－x0， ,1)， ＝(0, ，1)， 2 2− 2 3AQ QC=  0 0 3 2 3 1, ,4 4 4 2x y  +    2 10,0, 2      PQ 0 0 3 2 3, ,04 4 4x y  +    PQ ⊄ CM 02 y− BM 2 2 6.【2012 年.浙江卷.理 20】如图，在四棱锥 P－ABCD 中，底面是边长为 的菱形，∠BAD＝120°，且 PA⊥平面 ABCD， ，M，N 分别为 PB，PD 的中点． (1)证明：MN∥平面 ABCD； (2)过点 A 作 AQ⊥PC，垂足为点 Q，求二面角 A－MN－Q 的平面角的余弦值． 【答案】（1）详见解析；（2） . 【解析】(1)证明：因为 M，N 分别是 PB，PD 的中点， 所以 MN 是△PBD 的中位线．所以 MN∥BD． 又因为 MN 平面 ABCD，所以 MN∥平面 ABCD． (2)解：方法一：连结 AC 交 BD 于 O，以 O 为原点，OC，OD 所在直线为 x，y 轴，建立空间直角坐标系 O－ xy ，如图所示． 2 3 2 6PA = 33 33 由 ， 知 取 ＝5，得 n＝( ，0,5)．于是 cos〈m，n〉＝ ． 所以二面角 A­MN­Q 的平面角的余弦值为 ． 方法二：在菱形 ABCD 中，∠BAD=120°，得 AC=AB=BC=CD=DA，BD=AB． 5 3 3 6( )6 2 3QM = − − ， ， 5 3 3 6( )6 2 3QN = − ，， 5 3 3 6 0,6 2 3 5 3 3 6 0.6 2 3 x y z x y z − − + = − + + = 2 2 33 | | | | 33 ⋅ =⋅ m n m n 33 33 7.【2011 年.浙江卷.理 20】（本题满分 15 分）如图，在三棱锥 中， ，D 为 BC 的中点， PO⊥平面 ABC，垂足 O 落在线段 AD 上，已知 BC=8，PO=4，AO=3，OD=2 （Ⅰ）证明：AP⊥BC； P ABC− AB AC= （Ⅱ）在线段 AP 上是否存在点 M，使得二面角 A-MC-β 为直二面角？若存在，求出 AM 的长；若不存在，请 说明理由。 由 即 得 可取 由 ，得 解得 ，故 AM=3 综上所述，存在点 M 符合题意，AM=3。 法二（Ⅰ）证明： 又 因为 所以 平面 故 （Ⅱ）如图，在平面 内作 2 1 0, 0, AP n AC n  ⋅ = ⋅ =     2 2 2 2 3 4 0, 4 5 0, y z x y + = − + = 2 2 2 2 5 ,4 3 ,4 x y z y  =  = 2 (5,4, 3),n = − 1 2 0n n⋅ =  2 34 3 04 4 λ λ +− ⋅ =− 2 5 λ = ,AB AC D BC= 为 中点, ,AD BC∴ ⊥ ,PO ABC⊥ 平面 PO BC∴ ⊥ PO AD O∴ = BC ⊥ PAD BC PA⊥ PAB ,BM AP M⊥ 于 连结CM, 8.【2010 年.浙江卷.理 20】（本题满分 15 分）如图， 在矩形 中，点 分别在线段 上， .沿直线 将 翻折成 ，使平面 . （Ⅰ）求二面角 的余弦值； （Ⅱ）点 分别在线段 上，若沿直线 将四边形 向上翻折，使 与 重合，求线 段 的长。 【答案】（Ⅰ） （Ⅱ） 【解析】本题主要考察空间点、线、面位置关系，二面角等基础知识，空间向量的应用，同事考查空间想 ABCD ,E F ,AB AD 2 43AE EB AF FD= = = = EF AEF 'A EF 'A EF BEF⊥ 平面 'A FD C− − ,M N ,FD BC MN MNCD C 'A FM 3 3 21 4FM = 象能力和运算求解能力。 （Ⅰ）解：取线段 EF 的中点 H，连结 ，因为 = 及 H 是 EF 的中点，所以 , 方法二： 'A H 'A E 'A F 'A H EF⊥ （Ⅱ）解：设 , 因为翻折后， 与 重合， 所以 ， 而 ， 得 ，经检验，此时点 在线段 上， 所以 。 9.【2009 年.浙江卷.理 20】（本题满分 15 分）如图，平面 平面 ， 是以 为斜边的等腰直角三角形， 分别为 ， ， 的中点， ， ． （I）设 是 的中点，证明： 平面 ； （II）证明：在 内存在一点 ，使 平面 ，并求点 到 ， 的距离． FM x= C 'A 'CM A M= 2 2 2 2 28 (6 )CM DC DM x= + = + − 2 2 2 2 2 2' ' 'A M A H MH A H MG GH= + = + + 2(2 2)= 21 4x = N BC 21 4FM = PAC ⊥ ABC ABC∆ AC , ,E F O PA PB AC 16AC = 10PA PC= = G OC / /FG BOE ABO∆ M FM ⊥ BOE M OA OB 此有 ，即点 M 的坐标为 ，在平面直角坐标系 中， 的内部区域满足 不等式组 ，经检验，点 M 的坐标满足上述不等式组，所以在 内存在一点 ，使 平面 ，由点 M 的坐标得点 到 ， 的距离为 ．w.w.w c.o.m 10.【2016 高考浙江理数】(本题满分 15 分)如图,在三棱台 中,平面 平面 , ,BE=EF=FC=1,BC=2,AC=3. (I)求证：EF⊥平面 ACFD； (II)求二面角 B-AD-F 的平面角的余弦值. 0 0 94, 4x y= = − 94, ,04  −   xoy AOB∆ 0 0 8 x y x y >  <  − < ABO∆ M FM ⊥ BOE M OA OB 94, 4 ABC DEF− BCFE ⊥ ABC =90ACB∠  【答案】（I）证明见解析；（II） ． 【解析】 （II）方法一： 过点 作 ，连结 ． 3 4 F FQ ⊥ ΑΚ QΒ ， ， ， ， ， ． 因此， ， ， ． 设平面 的法向量为 ，平面 的法向量为 ． 由 ，得 ，取 ； 由 ，得 ，取 ． ] 于是， ． 所以，二面角 的平面角的余弦值为 ． ( )1,0,0Β ( )C 1,0,0− ( )0,0, 3Κ ( )1, 3,0Α − − 1 3,0,2 2  Ε    1 3F ,0,2 2  −    ( )C 0,3,0Α = ( )1,3, 3ΑΚ = ( )2,3,0ΑΒ = CΑ Κ ( )1 1 1, ,m x y z= ΑΒΚ ( )2 2 2, ,n x y z= C 0 0 m m Α ⋅ =ΑΚ ⋅ =     1 1 1 1 3 0 3 3 0 y x y z = + + = ( )3,0, 1m = − 0 0 n n ΑΒ⋅ =ΑΚ ⋅ =     2 2 2 2 2 2 3 0 3 3 0 x y x y z + = + + = ( )3, 2, 3n = − 3cos , 4 m nm n m n ⋅= =⋅      D FΒ − Α − 3 4 考点：1、线面垂直；2、二面角． 【方法点睛】解题时一定要注意二面角的平面角是锐角还是钝角，否则很容易出现错误．证明线面垂直的 关键是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方 形的对角线． 11. 【2015 高考浙江，文 18】（本题满分 15 分） 如图，在三棱锥 中， 在底 面 ABC 的射影为 BC 的中点，D 为 的中点. （1）证明： ； （2）求直线 和平面 所成的角的正弦值. 【答案】(1)略；(2) 【解析】 (1)利用线面垂直的定义得到线线垂直，根据线面垂直的判定证明直线与平面垂直； (2)通过添加辅助线，证明 平面 ，以此找到直线与平面所成角的平面角 ，在直角三角 形 中通过确定边长，计算 的正弦值. 1 1 1ABC A B C- 1 1ABC 90 AB AC 2,AA 4,A∠ = = = =， 1 1B C 1 1D A BCA ⊥ 平面 1A B 1 1B CB C 7 8 1A F ⊥ 1 1BB C C 1A BF∠ 1A BF 1A BF∠ (2)作 ，垂足为 ，连结 . 因为 平面 ，所以 . 因为 ，所以 平面 . 所以 平面 . 所以 为直线 与平面 所成角的平面角. 由 ，得 . 由 平面 ，得 . 由 ，得 . 所以 【考点定位】1.空间直线、平面垂直关系的证明；2.直线与平面所成的角. 12.【2014 年.浙江卷.文 20】（本小题满分 15 分） 1A F DE⊥ F FΒ AE ⊥ 1A BC 1BC A E⊥ BC AE⊥ BC ⊥ 1AA DE 1 1,BC A F A F⊥ ⊥ 1 1BB C C 1A BF∠ 1A B 1 1BB C C 2, 90AB AC CAB= = ∠ =  2EA EB= = AE ⊥ 1A BC 1 1 14, 14A A A B A E= = = 1 1 14, 2, 90DE BB DA EA DA E= = = = ∠ =  1 7 2A F = 1 7sin 8A BF∠ = 如图，在四棱锥 中，平面 平面 ； ， ， ， . （1）证明： 平面 ； （2）求直线 与平面 所成的角的正切值. 【答案】（1）详见解析；（2） . 【解析】 BCDEA− ABC ⊥ BCDE 90CDE BED∠ = ∠ = ° 2AB CD= = 1DE BE= = 2AC = AC ⊥ BCDE AE ABC A D E B C 13 13 在 中， ， ，得 ， 在 中，由 ， 得 ， 所以直线 与平面 所成的角的正切值是 . 考点：空间点、线、面的位置关系，线面所成的角. 13.【2013 年.浙江卷.文 20】(本题满分 15 分)如图，在四棱锥 P－ABCD 中，PA⊥平面 ABCD，AB＝BC＝ 2，AD＝CD＝ ，PA＝ ，∠ABC＝120°，G 为线段 PC 上的点． (1)证明：BD⊥平面 APC； (2)若 G 为 PC 的中点，求 DG 与平面 APC 所成的角的正切值； (3)若 G 满足 PC⊥平面 BGD，求 的值． 【答案】(1) 详见解析；(2) . (3) 【解析】(1)设点 O 为 AC，BD 的交点． 由 AB＝BC，AD＝CD，得 BD 是线段 AC 的中垂线．所以 O 为 AC 的中点，BD⊥AC. 又因为 PA⊥平面 ABCD，BD 平面 ABCD，所以 PA⊥BD.所以 BD⊥平面 APC. (2)连结 OG.由(1)可知 OD⊥平面 APC，则 DG 在平面 APC 内的射影为 OG，所以∠OGD 是 DG 与平面 APC 所成的角． ACFRT∆ 2=AC 2 23=CF 2 26=AF AEFRt∆ 2 2=EF 2 26=AF 13 13tan =∠EAF AE ABC 13 13 7 3 PG GC 4 3 3 3 2 PG GC = ⊂ 14.【2012 年.浙江卷.文 20】如图，在侧棱垂直底面的四棱柱 ABCD －A1B1C1D1 中，AD∥BC，AD⊥AB， ，AD=2，BC=4，AA1=2，E 是 DD1 的中点，F 是平面 B1C1E 与直线 AA1 的交点． (1)证明：①EF∥A1D1； ②BA1⊥平面 B1C1EF； ] (2)求 BC1 与平面 B1C1EF 所成的角的正弦值． 【答案】(1)详见解析； (2) ． 【解析】(1)证明：①因为 C1B1∥A1D1，C1B1 平面 ADD1A1， 2AB = 30 15 15.【2011 年.浙江卷.文 20】（本题满分 14 分）如图，在三棱锥 中， ， 为 的中 点， ⊥平面 ，垂足 落在线段 上. （Ⅰ）证明： ⊥ ； （Ⅱ）已知 ， ， ， .求二面角 的大小. P ABC− AB AC= D BC PO ABC O AD AP BC 8BC = 4PO = 3AO = 2OD = B AP C− − 【答案】（Ⅰ）详见解析；（Ⅱ）二面角 的大小为 同理 ，因为 所以 即二面角 的大小为 16.【2010 年.浙江卷.文 20】（本题满分 14 分）如图，在平行四边形 ABCD 中，AB=2BC，∠ABC=120°。E 为 线段 AB 的中点，将△ADE 沿直线 DE 翻折成△A’DE，使平面 A’DE⊥平面 BCD，F 为线段 A’C 的中点。 （Ⅰ）求证：BF∥平面 A’DE； B AP C− − 90 4 2CM = 2 2 2BM CM BC+ = 90BMC∠ =  B AP C− − 90 （Ⅱ）设 M 为线段 DE 的中点，求直线 FM 与平面 A’DE 所成角的余弦值。 【答案】(Ⅰ)详见解析；（Ⅱ）直线 FM 与平面 A′DE 所成角的余弦值为 . 所以 BF//平面 （Ⅱ）解：在平行四边形,ABCD 中，设 BC=a 则 AB=CD=2a, AD=AE=EB=a, 连 CE 因为 在△BCE 中，可得 CE= a, 1 2 'A DE 0120ABC∠ = 3 17.【2009 年.浙江卷.文 19】（本题满分 14 分） 如 图 ， 平 面 ， ， ， ， 分 别 为 的中点． （I）证明： 平面 ； （II）求 与平面 所成角的正弦值． 【答案】（Ⅰ）见解析；（Ⅱ） 【解析】（Ⅰ）证明：连接 ， 在 中， 分别是 的中点，所以 ， DC ⊥ ABC / /EB DC 2 2AC BC EB DC= = = = 120ACB∠ =  ,P Q ,AE AB / /PQ ACD AD ABE 5 5 CQDP, ABE∆ QP, ABAE, BEPQ 2 1//== 又 18.【2016 高考浙江文数】如图，在三棱台 ABC–DEF 中，平面 BCFE⊥平面 ABC，∠ACB=90°，BE=EF=FC=1， BC=2，AC=3. （Ⅰ）求证：BF⊥平面 ACFD； （Ⅱ）求直线 BD 与平面 ACFD 所成角的余弦值. 【答案】（1）证明详见解析；（2） . 【解析】 试题分析：本题主要考查空间点、线、面位置关系，线面角等基础知识，同时考查空间想象能力和运算求 解能力． 试题解析：（Ⅰ）延长 相交于一点 ，如图所示. 因为平面 平面 ，且 ，所以 平面 ，因此， . 又因为 ， ， ，所以 为等边三角形，且 为 的中点，则 所以 平面 . 21 7 , ,AD BE CF K BCFE ⊥ ABC AC BC⊥ AC ⊥ BCK BF AC⊥ //EF BC 1BE EF FC= = = 2BC = BCK△ F CK BF CK⊥ BF ⊥ ACFD （Ⅱ）因为 平面 ，所以 是直线 与平面 所成的角. 在 中， ，得 . 所以，直线 与平面 所成的角的余弦值为 . 【考点】空间点、线、面位置关系、线面角. 【方法点睛】解题时一定要注意直线与平面所成的角的范围，否则很容易出现错误．证明线面垂直的关键 是证明线线垂直，证明线线垂直常用的方法是直角三角形、等腰三角形的“三线合一”和菱形、正方形的 对角线． 【对症下药】 1.利用“坐标法解(证)立体几何题的步骤 第一步，建立坐标系．通常把两两互相垂直且相交于同一点的三条直线作为三条坐标轴，它们的交点 作为原点，并选取适当的单位长度； 第二步，表示点的坐标．将题中相关点用坐标表示，这一步是解(证)几何题的关键； 第三步，表示向量的坐标．根据点的坐标可以求出所需要的向量的坐标，即用表示向量的终点坐标减 去始点坐标； 第四步，求出问题的解．将点或向量的坐标代入公式(夹角公式、距离公式等)； 第五步，得出结论．根据上一步所求得的结果，进一步得出问题的正确结论． 上述五步中第二步是最关键一步，点的坐标决定着向量的坐标，从而决定着后续计算的对错，也就意 味着解题的成功与失败，因此特强调如下两点： 2.如何确定空间点的坐标 空间点的坐标是有序实数组 ，其中的三个数 ， ， 包含坐标的符号与坐标的绝对值．要确 定一个点的坐标，应先判断三个坐标的符号，然后再确定三个坐标的绝对值． (1)判断点的坐标的符号 点在坐标平面上的射影位于坐标轴的正方向，则这点对应的坐标的符号为正，否则为负．如位于 轴 正方向，则横坐标为正；位于 轴负方向，则竖坐标为负． (2)确定点的坐标的绝对值 过这个点向三个坐标平面作垂线，看垂线段平行于哪个轴，则这条线段的长度就是该点哪个坐标的绝 BF ⊥ ACK BDF∠ BD ACFD Rt BFD△ 33, 2BF DF= = 21cos 7BDF∠ = BD ACFD 21 7 ( ), ,x y z x y z x z 对值．如这条垂线段平行于 轴且长度为 ，则该点的纵坐标的绝对值是 ；如这条垂线段平行于 轴且长 度为 ，则该点的竖坐标的绝对值是 ． 3.常见特殊点的坐标特点 (1)坐标轴上点的坐标的特点 ① 轴上的点的纵坐标和竖坐标均为 0，形如 ． ② 轴上的点的横坐标和竖坐标均为 0，形如 ． ③ 轴上的点的横坐标和纵坐标均为 0，形如 ． (2)坐标平面上点的坐标的特点 ① 平面上所有点的竖坐标是 0，形如 ． ② 平面上所有点的横坐标是 0，形如 ． ③ 平面上所有点的纵坐标是 0，形如 ． (3)非特殊点(既不在坐标轴上也不在坐标平面内的点)的坐标设法 如果 是线段 上的任一点， ， ，其中 ， ， ， ， ， 均已 知，设 ，并由 在线段 上知存在实数 ，使得 ，即 ， 所以 ， ， ． 这样 点坐标就可只用一个参数 来表示了，即 ，这样 设的目的是便于求参数 (只列一个关于 的方程即可)． 【考题预测】 1.如图，在长方体 中， ， ， 、 分别是 、 的中点．证 明 、 、 、 四点共面，并求直线 与平面 所成的角的正弦值大小. 【答案】 1 1 1 1CD C DΑΒ − Α Β 1 1ΑΑ = D 2ΑΒ = Α = Ε F ΑΒ CΒ 1 Α 1C F Ε 1CD 1 1C FΑ Ε 15 15 y a a z a a x ( ),0,0a y ( )0, ,0a z ( )0,0,a xOy ( ), ,0a b yOz ( )0, ,a b xOz ( ),0,a b P AB ( )1 1 1, ,A x y z ( )2 2 2, ,B x y z 1x 2x 1y 2y 1z 2z ( ), ,P x y z P AB t AP t AB=  ( ) ( )1 1 1 2 1 2 1 2 1, , , ,x x y y z z t x x y y z z− − − = − − − ( )2 11x tx t x= + − ( )2 11y ty t y= + − ( )2 11z tz t z= + − P t ( ) ( ) ( )( )2 1 2 1 2 11 , 1 , 1P tx t x ty t y tz t z+ − + − + − t t 2.如图，三棱柱 中， ， ， 分别为棱 的中点. （1）在平面 内过点 作 平面 交 于点 ，并写出作图步骤，但不要求证明. （2）若侧面 侧面 ，求直线 与平面 所成角的正弦值. 1 1 1ABC A B C− 0 1 1 1 1 160 , 4B A A C A A AA AC∠ = ∠ = = = 2AB = ,P Q 1,AA AC ABC A / /AM 1PQB BC M 1 1ACC A ⊥ 1 1ABB A 1 1AC 1PQB ] 【答案】（1）见解析（2） （2）连结 ，∵ ，∴ 为正三角形. 39 13 1 1,PC AC 0 1 1 1 1 14, 60AA AC AC C A A= = = ∠ = 1 1AC A∆ ∵ 为 的中点，∴点 的坐标为 ， ∴ . ∵ ，∴ ，∴ ， 设平面 的法向量为 ， 由 得 ， 令 ，得 ，所以平面 的一个法向量为 . 设直线 与平面 所成角为 ， 则 ， Q AC Q ( )0, 3, 3− ( ) ( )1 1 0, 2,2 3 , 0, 3, 3AC PQ= − = −  0 1 1 1 12, 60A B AB B A A= = ∠ = ( )1 3,1,0B ( )1 3,1,0PB = 1PQB ( ), ,m x y z= 1 · 0{ · 0 PQ m PB m = =     3 3 0{ 3 0 y z x y − + = + = 1x = 3, 3y z= − = − 1PQB ( )1, 3, 3m = − − 1 1AC 1PQB a 1 1 1 1 1 1 · 39sin cos , 13 AC mAC m AC m α = 〈 〉 = =      即直线 与平面 所成角的正弦值为 . 3.如图，在四棱锥 P-ABCD 中，AB//CD，且 . （1）证明：平面 PAB⊥平面 PAD； （2）若 PA=PD=AB=DC， ，求二面角 A-PB-C 的余弦值. 【解析】 试题解析：（1）由已知 ，得 AB⊥AP，CD⊥PD. 由于 AB∥CD ，故 AB⊥PD ，从而 AB⊥平面 PAD. 又 AB 平面 PAB，所以平面 PAB⊥平面 PAD. 1 1AC 1PQB 39 13 90BAP CDP∠ = ∠ =  90APD∠ =  90BAP CDP∠ = ∠ = ° ⊂ 可取 . 则 ， ] 所以二面角 的余弦值为 . (1,0,1)=m 3cos , | || | 3 ⋅= = −< > n mn m n m A PB C− − 3 3 − 4.如图，四棱锥 P-ABCD 中，侧面 PAD 为等比三角形且垂直于底面 ABCD， E 是 PD 的中点。 （1）证明：直线 平面 PAB； （2）点 M 在棱 PC 上，且直线 BM 与底面 ABCD 所成角为 ，求二面角 的余弦值。 【答案】(1)证明略； (2) 。 【解析】 试题解析： （1）取 的中点 ，连结 ， 。 因为 是 的中点，所以 ∥ , ,由 得 ∥ ，又 ,所以 。四边形 为平行四边形， ∥ 。 又 平面 ， 平面 ，故 平面 。 （2）由已知得 ,以 A 为坐标原点， 的方向为 x 轴正方向， 为单位长， 建立如图所示的空间直角坐标系 ， o1 , 90 ,2AB BC AD BAD ABC= = ∠ = ∠ = / /CE o45 M AB D− − 10 5 PA F EF BF E PD EF AD 1 2EF AD= 90BAD ABC∠ = ∠ =  BC AD 1 2BC AD= EF BC∥ BCEF CE BF BF ⊂ PAB CE ⊄ PAB CE∥ PAB BA AD⊥ AB AB A xyz− 5.如图，几何体是圆柱的一部分，它是由矩形 （及其内部）以 边所在直线为旋转轴旋转 得 到的， 是 的中点. （Ⅰ）设 是 上的一点，且 ，求 的大小； （Ⅱ）当 ， ，求二面角 的大小. 【答案】（Ⅰ） .（Ⅱ） . ABCD AB 120° G DF P CE AP BE⊥ CBP∠ 3AB = 2AD = E AG C− − 30CBP∠ = ° 60° 思路二： 以 为坐标原点，分别以 ， ， 所在的直线为 ， ， 轴，建立如图所示的空间直角坐标系. 写出相关点的坐标，求平面 的一个法向量 ，平面 的一个法向 [ 计算 即得. …… （Ⅱ）解法一： B BE BP BA x y z AEG 1 1 1( , , )m x y z= ACG 2 2 2( , , )n x y z= 1cos , | | | | 2 m nm n m n ⋅< >= =⋅