2019届二轮复习(理)第九章第57讲 椭Բ学案(江苏专用)
第57讲 椭 圆
考试要求 1.椭圆的实际背景,椭圆在刻画现实世界和解决实际问题中的作用(A级要求);2.椭圆的定义,几何图形,标准方程及简单几何性质(B级要求).
诊 断 自 测
1.思考辨析(在括号内打“√”或“×”)
(1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭圆.( )
(2)椭圆的离心率e越大,椭圆就越圆.( )
(3)椭圆既是轴对称图形,又是中心对称图形.( )
(4)方程mx2+ny2=1(m>0,n>0,m≠n)表示的曲线是椭圆.( )
(5)+=1(a>b>0)与+=1(a>b>0)的焦距相同.( )
解析 (1)由椭圆的定义知,当该常数大于F1F2时,其轨迹才是椭圆,而常数等于F1F2时,其轨迹为线段F1F2,常数小于F1F2时,不存在这样的图形.
(2)因为e===,所以e越大,则越小,椭圆就越扁.
答案 (1)× (2)× (3)√ (4)√ (5)√
2.(2017·浙江卷改编)椭圆+=1的离心率是 .
解析 由已知,a=3,b=2,则c==,所以e==.
答案
3.(教材改编)椭圆+=1的焦距为4,则m= .
解析 由题意知
或
解得m=4或m=8.
答案 4或8
4.(选修1-1P30习题3改编)经过A,B两点的椭圆的标准方程为 .
解析 设椭圆方程为+=1(a>0,b>0),将点A,B代入得+=1,
+=1,解得b2=1,a2=8,
所以椭圆方程为+y2=1.
答案 +y2=1
5.(教材改编)已知点P是椭圆+=1上y轴右侧的一点,且以点P及焦点F1,F2为顶点的三角形的面积等于1,则点P的坐标为 .
解析 设P(x,y),由题意知c2=a2-b2=5-4=1,
所以c=1,则F1(-1,0),F2(1,0),由题意可得点P到x轴的距离为1,所以y=±1,把y=±1代入+=1,
得x=±,又x>0,所以x=,所以P点坐标为或.
答案 或
知 识 梳 理
1.椭圆的概念
平面内到两个定点F1,F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆,两个定点F1,F2叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
集合P={M|MF1+MF2=2a},F1F2=2c,其中a>0,c>0,且a,c为常数:
(1)若a>c,则集合P为椭圆;
(2)若a=c,则集合P为线段;
(3)若a
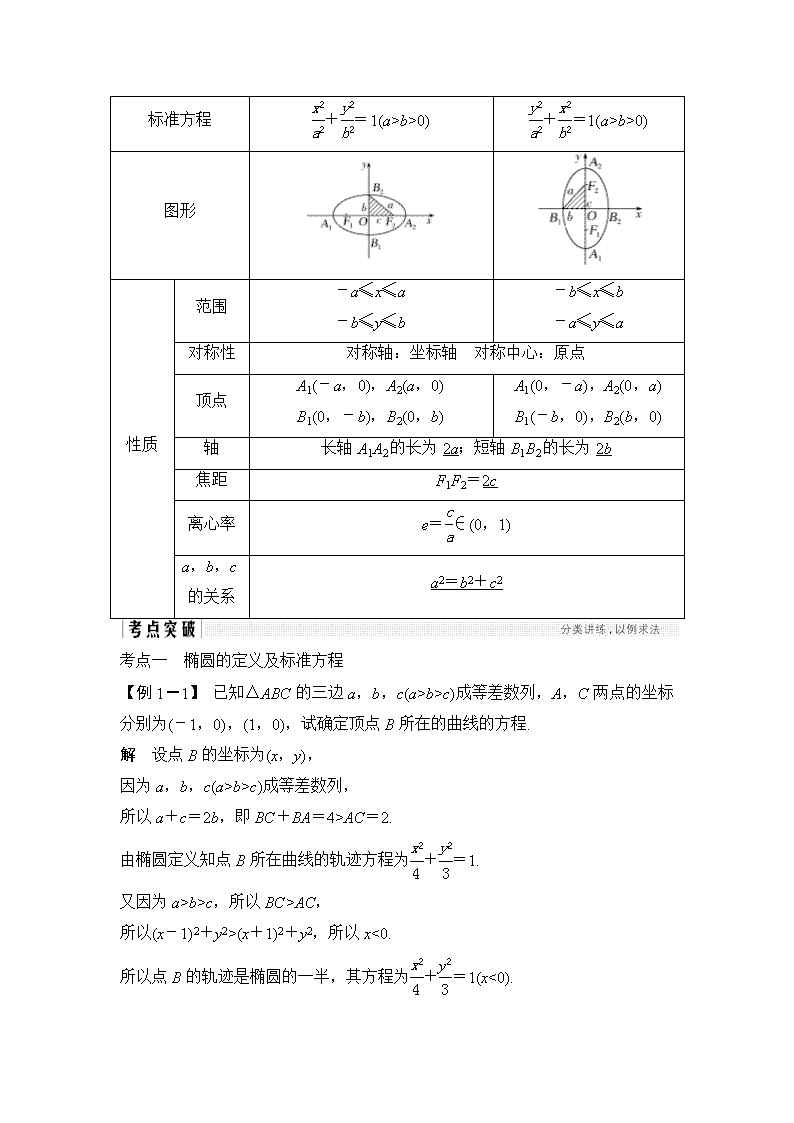
b>0)
+=1(a>b>0)
图形
性质
范围
-a≤x≤a
-b≤y≤b
-b≤x≤b
-a≤y≤a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
轴
长轴A1A2的长为2a;短轴B1B2的长为2b
焦距
F1F2=2c
离心率
e=∈(0,1)
a,b,c的关系
a2=b2+c2
考点一 椭圆的定义及标准方程
【例1-1】 已知△ABC的三边a,b,c(a>b>c)成等差数列,A,C两点的坐标分别为(-1,0),(1,0),试确定顶点B所在的曲线的方程.
解 设点B的坐标为(x,y),
因为a,b,c(a>b>c)成等差数列,
所以a+c=2b,即BC+BA=4>AC=2.
由椭圆定义知点B所在曲线的轨迹方程为+=1.
又因为a>b>c,所以BC>AC,
所以(x-1)2+y2>(x+1)2+y2,所以x<0.
所以点B的轨迹是椭圆的一半,其方程为+=1(x<0).
又当x=-2时,点B,A,C在同一直线上,不能构成△ABC,所以x≠-2.
所以顶点B的轨迹方程为+=1(-2b>0).
∵椭圆过P(3,0),∴+=1,即a=3,
又2a=3×2b,∴b=1,∴椭圆方程为+y2=1.
若焦点在y轴上,设方程为+=1(a>b>0).
∵椭圆过点P(3,0),∴+=1,即b=3.
又2a=3×2b,∴a=9,∴椭圆方程为+=1.
∴所求椭圆的方程为+y2=1或+=1.
(2)设椭圆方程为mx2+ny2=1(m>0,n>0且m≠n).
∵椭圆经过点P1,P2,∴点P1,P2的坐标适合椭圆方程.
即
①②两式联立,解得
∴所求椭圆方程为+=1.
答案 (1)+y2=1或+=1
(2)+=1
【例1-3】 已知F1,F2是椭圆C:+=1(a>b>0)的两个焦点,P为椭圆C
上的一点,且1⊥2.若△PF1F2的面积为9,则b= .
解析 设PF1=r1,PF2=r2,
则
因为2r1r2=(r1+r2)2-(r+r)
=4a2-4c2=4b2,
又因为S△PF1F2=r1r2=b2=9,
所以b=3.
答案 3
规律方法 (1)求椭圆的方程多采用定义法和待定系数法,利用椭圆的定义定形状时,一定要注意常数2a>F1F2这一条件.
(2)求椭圆标准方程的基本方法是待定系数法,具体过程是先定形,再定量,即首先确定焦点所在位置,然后再根据条件建立关于a,b的方程组.如果焦点位置不确定,要考虑是否有两解,有时为了解题方便,也可把椭圆方程设为mx2+ny2=1(m>0,n>0,m≠n)的形式.
(3)当P在椭圆上时,与椭圆的两焦点F1,F2组成的三角形通常称为“焦点三角形”,利用定义可求其周长;利用定义和余弦定理可求PF1·PF2;通过整体代入可求其面积等.
【训练1】 已知动圆M与圆F:x2+(y-2)2=1外切,与圆N:x2+y2+4y-77=0内切,求动圆圆心M所在的曲线C的方程.
解 因为圆N:x2+y2+4y-77=0,
即x2+(y+2)2=81,所以N(0,-2),半径为9.
设动圆半径为R,则MF=R+1,MN=9-R,
所以MF+MN=10>FN=4,所以动点M所在的曲线是以F,N为焦点、长轴长为10的椭圆,其方程为+=1.
考点二 椭圆的几何性质
【例2-1】 (2016·全国Ⅲ卷改编)已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A
的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为 .
解析 设M(-c,m),则E ,OE的中点为D,则D ,又B,D,M三点共线,所以=,a=3c,e=.
答案
【例2-2】 已知点F1,F2是椭圆x2+2y2=2的左,右焦点,点P是该椭圆上的一个动点,那么|1+2|的最小值是 .
解析 设P(x0,y0),则1=(-1-x0,-y0),
=(1-x0,-y0),∴1+2=(-2x0,-2y0),
∴|1+2|=
=2
=2,
∵点P在椭圆上,∴0≤y≤1,
∴当y=1时,|1+2|取最小值2.
答案 2
规律方法 (1)利用椭圆几何性质的注意点及技巧
①注意椭圆几何性质中的不等关系
在求与椭圆有关的一些量的范围,或者最大值、最小值时,经常用到椭圆标准方程中x,y的范围,离心率的范围等不等关系.
②利用椭圆几何性质的技巧
求解与椭圆几何性质有关的问题时,要结合图形进行分析,当涉及顶点、焦点、长轴、短轴等椭圆的基本量时,要理清它们之间的内在联系.
(2)求椭圆的离心率问题的一般思路
求椭圆的离心率或其范围时,一般是依据题设得出一个关于a,b,c的等式或不等式,利用a2=b2+c2消去b,即可求得离心率或离心率的范围.
【训练2】 (2016·江苏卷)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是 .
解析 联立方程组解得B、C两点坐标为
B,C,又F(c,0),
则=,=,
又由∠BFC=90°,可得·=0,代入坐标可得
c2-a2+=0,①
又因为b2=a2-c2.
代入①式可化简为=,则椭圆离心率为e===.
答案
考点三 直线与椭圆的位置关系
【例3】 (2015·江苏卷)如图,在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的离心率为,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
解 (1)由题意,得=且c+=3,
解得a=,c=1,则b=1,
所以椭圆的标准方程为+y2=1.
(2)当AB⊥x轴时,AB=,又CP=3,不合题意.
当AB与x轴不垂直时,设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2),
将AB的方程代入椭圆方程,
得(1+2k2)x2-4k2x+2(k2-1)=0,
则x1,2=,
C的坐标为,且
AB==
=.
若k=0,则线段AB的垂直平分线为y轴,与左准线平行,不合题意.
从而k≠0,故直线PC的方程为
y+=-,
则P点的坐标为,
从而PC=.
因为PC=2AB,所以=,
解得k=±1.
此时直线AB的方程为y=x-1或y=-x+1.
规律方法 与椭圆有关的综合问题,往往与其他知识相结合,解决这类问题的常规思路是联立直线方程与椭圆方程,解方程组求出直线与椭圆的交点坐标
,然后根据所给的向量条件再建立方程,解决相关问题.涉及弦中点问题用“点差法”解决往往更简单.
【训练3】 (2018·南通调研)如图,已知椭圆+=1(a>b>0)的右顶点为A(2,0),点P在椭圆上(e为椭圆的离心率).
(1)求椭圆的标准方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足=λ,且·=0,求实数λ的值.
解 (1)由条件,a=2,e=,代入椭圆方程,得+=1.
∵b2+c2=4,∴b2=1,c2=3.
∴椭圆的标准方程为+y2=1.
(2)设直线OC的斜率为k,则直线OC方程为y=kx,
代入椭圆方程+y2=1,即x2+4y2=4,
得(1+4k2)x2=4,∴xC=.
则C.
又直线AB方程为y=k(x-2),
代入椭圆方程x2+4y2=4,
得(1+4k2)x2-16k2x+16k2-4=0.
∵xA=2,∴xB=,则B.
∵·=0,∴·+·=0.
∴k2=,∵C在第一象限,∴k>0,k=.
∵=,
==,
由=λ,得λ=.
∵k=,∴λ=.
一、必做题
1.(2018·苏北四市联考)已知椭圆的中心在原点,离心率e=,且它的一个焦点与抛物线y2=-4x的焦点重合,则此椭圆方程为 .
解析 依题意可设椭圆的标准方程为+=1(a>b>0),由已知可得抛物线的焦点为(-1,0),所以c=1,又离心率e==,解得a=2,b2=a2-c2=3,所以椭圆方程为+=1.
答案 +=1
2.(2017·全国Ⅲ卷改编)已知椭圆C:+=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则C的离心率为 .
解析 以线段A1A2为直径的圆是x2+y2=a2,直线bx-ay+2ab=0与圆相切,所以圆心(0,0)到直线的距离d==a,整理为a2=3b2,即a2=3(a2-c2)⇒2a2=3c2,即=,e==.
答案
3.(2018·青岛月考)已知A1,A2分别为椭圆C:+=1(a>b>0)的左,右顶点,P
是椭圆C上异于A1,A2的任意一点,若直线PA1,PA2的斜率的乘积为-,则椭圆C的离心率为 .
解析 设P(x0,y0),则·=-,
化简得+=1,
则=,e===.
答案
4.已知P为椭圆+=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则PM+PN的最小值为 .
解析 由题意知椭圆的两个焦点F1,F2分别是两圆的圆心,且PF1+PF2=10,从而PM+PN的最小值为PF1+PF2-1-2=7.
答案 7
5.若椭圆+=1(a>0,b>0)的焦点在x轴上,过点(2,1)作圆x2+y2=4的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程为 .
解析 设切点坐标为(m,n),
则·=-1,
即m2+n2-n-2m=0.
∵m2+n2=4,∴2m+n-4=0,
即直线AB的方程为2x+y-4=0.
∵直线AB恰好经过椭圆的右焦点和上顶点,
∴2c-4=0,b-4=0,解得c=2,b=4,
∴a2=b2+c2=20,
∴椭圆方程为+=1.
答案 +=1
6.(2018·南昌模拟)已知椭圆:+x2=1,过点P的直线与椭圆相交于A,B两点,且弦AB被点P平分,则直线AB的方程为 .
解析 设A(x1,y1),B(x2,y2),因为A,B在椭圆+x2=1上,所以
两式相减得+x-x=0,
即+(x1-x2)(x1+x2)=0,
又弦AB被点P平分,
所以x1+x2=1,y1+y2=1,
将其代入上式,得+x1-x2=0,
得=-9,
即直线AB的斜率为-9,所以直线AB的方程为
y-=-9,
即9x+y-5=0.
答案 9x+y-5=0
7.(2018·宿迁模拟)已知F1、F2是椭圆+y2=1的两个焦点,P为椭圆上一动点,则使PF1·PF2取得最大值的点P为 .
解析 由椭圆定义得PF1+PF2=2a=4,
∴PF1·PF2≤=4,
当且仅当PF1=PF2=2,
即P(0,-1)或(0,1)时,PF1·PF2取得最大值.
答案 (0,1)或(0,-1)
8.(2018·连云港质检)椭圆+y2=1的左,右焦点分别为F1,F2,点P为椭圆上一动点,若∠F1PF2为钝角,则点P的横坐标的取值范围是 .
解析 设椭圆上一点P的坐标为(x,y),
则=(x+,y),=(x-,y).
∵∠F1PF2为钝角,∴·<0,
即x2-3+y2<0,①
∵y2=1-,代入①得x2-3+1-<0,
x2<2,∴x2<.
解得-b>0)的右焦点为F,右顶点,上顶点分别为A,B,且AB=BF.
(1)求椭圆C的离心率;
(2)若斜率为2的直线l过点(0,2),且l交椭圆C于P,Q两点,OP⊥OQ,求直线l的方程及椭圆C的方程.
解 (1)由已知AB=BF,
即=a,
4a2+4b2=5a2,4a2+4(a2-c2)=5a2,
∴e==.
(2)由(1)知a2=4b2,∴椭圆C:+=1.
设P(x1,y1),Q(x2,y2),
直线l的方程为y-2=2(x-0),即2x-y+2=0.
由消去y,
得x2+4(2x+2)2-4b2=0,
即17x2+32x+16-4b2=0.
Δ=322+16×17(b2-4)>0,解得b>.
x1+x2=-,x1x2=.
∵OP⊥OQ,∴·=0,
即x1x2+y1y2=0,x1x2+(2x1+2)(2x2+2)=0,
5x1x2+4(x1+x2)+4=0.
从而-+4=0,
解得b=1,满足b>.
∴椭圆C的方程为+y2=1.
10.(南通、泰州市2018届高三第一次调研)如图,在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的离心率为,焦点到相应准线的距离为1.
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线y=于点Q,求+的值.
解 (1)由题意得=,-c=1,
解得a=,c=1,b=1.
所以椭圆的方程为+y2=1.
(2)由题意知OP的斜率存在.
当OP的斜率为0时,OP=,OQ=,所以+=1.当OP的斜率不为0时,设直线OP方程为y=kx.
由得x2=2,解得x2=,所以y2=,
所以OP2=x2+y2=.因为OP⊥OQ,所以直线OQ的方程为y=-x.
由得x=-k,所以OQ2=2k2+2.所以+=+=1.
综上,可知+=1.
二、选做题
11.(2018·苏州质检)设A1,A2为椭圆+=1(a>b>0)的左,右顶点,若在椭圆上存在异于A1,A2的点P,使得·2=0,其中O为坐标原点,则椭圆的离心率e的取值范围是 .
解析 A1(-a,0),A2(a,0),
设P(x,y),则=(-x,-y),2=(a-x,-y),
∵·2=0,∴(a-x)(-x)+(-y)(-y)=0,
∴y2=ax-x2>0,∴0.
又0<<1,∴<<1.
答案
12.(南京市、盐城市2018届高三第一次模拟)在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆E:+=1(0
查看更多