2017届高考文科数学(全国通用)二轮文档讲义:第3编应试技能专训-1客观题专练
第三步 应试技能专训
一、客观题专练
(一)
一、选择题
1.设U=R,集合A=,B={x∈R|0
0),故选C.
4.已知数列{an}是公差为3的等差数列,且a1,a2,a5成等比数列,则a10等于( )
A.14 B.
C. D.32
答案 C
解析 由题意可得a=a1·a5,即(a1+3)2=a1(a1+4×3),解之得a1=,故a10=+(10-1)×3=,故选C.
5.已知变量x,y满足约束条件则z=2x+y的最大值为( )
A.1 B.2
C.3 D.4
答案 B
解析 画出可行域得知,当直线y=z-2x过点(1,0)时,z取得最大值2.
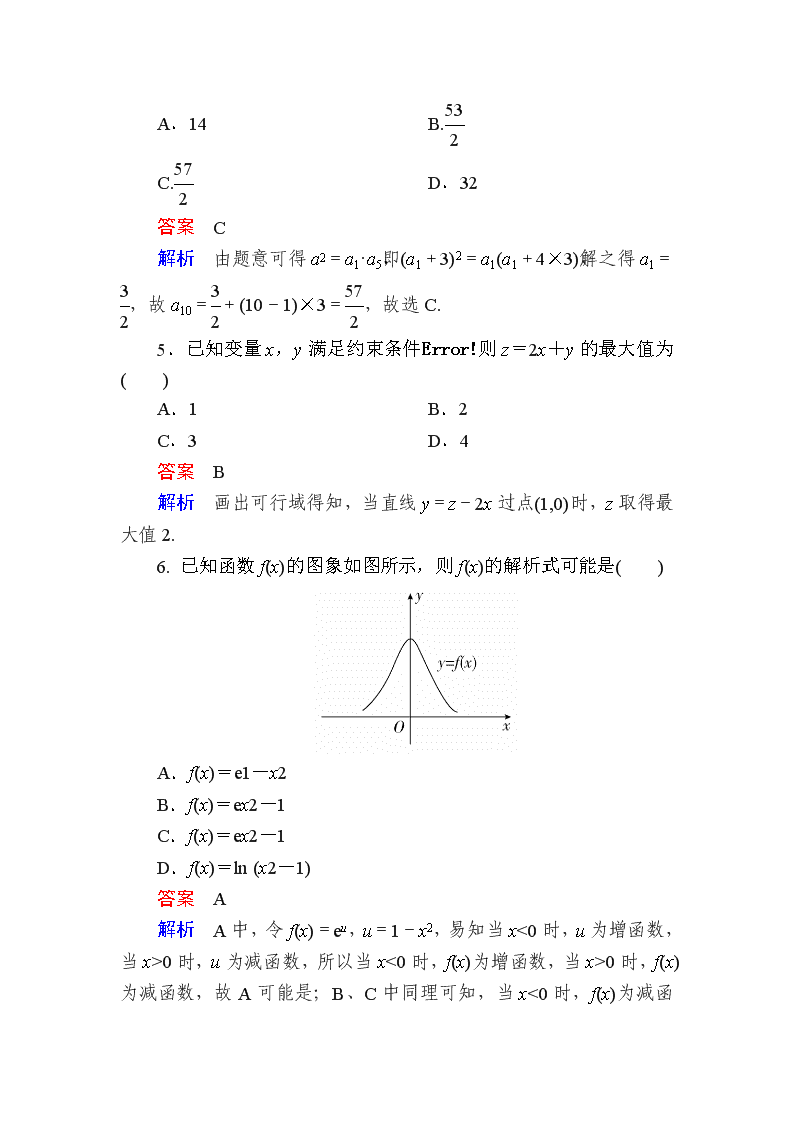
6. 已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
A.f(x)=e1-x2
B.f(x)=ex2-1
C.f(x)=ex2-1
D.f(x)=ln (x2-1)
答案 A
解析 A中,令f(x)=eu,u=1-x2,易知当x<0时,u为增函数,当x>0时,u为减函数,所以当x<0时,f(x)为增函数,当x>0时,f(x)为减函数,故A可能是;B、C中同理可知,当x<0时,f(x)为减函数,当x>0时,f(x)为增函数,故B、C不是;D中,当x
=0时,无意义,故D不是,选A.
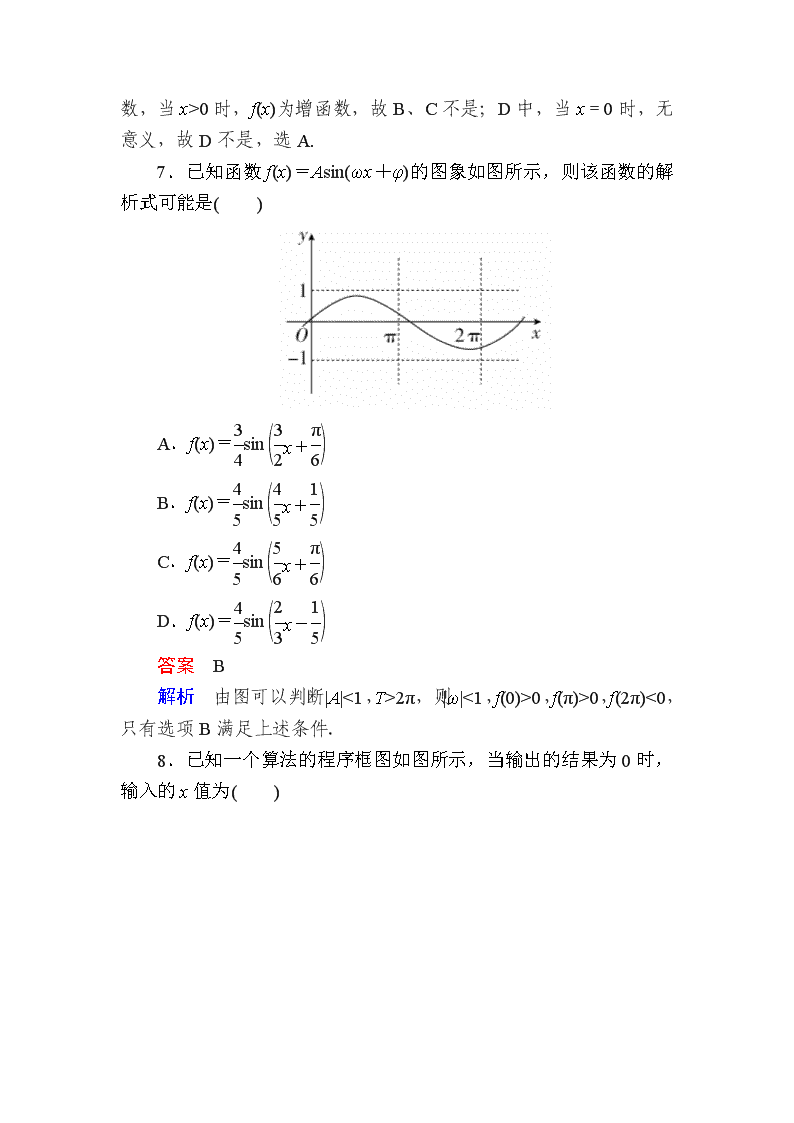
7.已知函数f(x)=Asin(ωx+φ)的图象如图所示,则该函数的解析式可能是( )
A.f(x)=sin
B.f(x)=sin
C.f(x)=sin
D.f(x)=sin
答案 B
解析 由图可以判断|A|<1,T>2π,则|ω|<1,f(0)>0,f(π)>0,f(2π)<0,只有选项B满足上述条件.
8.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x值为( )
A.-2 B.-2或-1
C.1或-3 D.-2或
答案 D
解析 当x≤0时,由y=x-4=0得x=-2;
当x>0时,由y=log3x+1=0得x=.
第三编/第三步 应试技能专训金版教程|大二轮·文数
9. 高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
A.
B.
C.
D.
答案 C
解析 由侧视图、俯视图知该几何体是高为2、底面积为×2×(2+4)=6的四棱锥,其体积为4.易知直三棱柱的体积为8,则该几何体的体积是原直三棱柱的体积的=,故选C.
10.[2016·贵阳监测]已知双曲线-=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F(-2,0),则双曲线的离心率是( )
A. B.
C. D.
答案 B
解析 设P(x0,),因为函数y=的导数为y′=,所以切线的斜率为.又切线过双曲线的左焦点F(-2,0),所以=,解得x0=2,所以P(2,).因为点P在双曲线上,所以-=1 ①.又c2=22=a2+b2 ②,联立①②解得a=或a=2(舍),所以e===,故选B.
11.[2016·山西四校联考]在正三棱锥S-ABC中,M是SC的中点,且AM⊥SB,底面边长AB=2,则正三棱锥S-ABC的外接球的表面积为( )
A.6π B.12π
C.32π D.36π
答案 B
解析 如图,取CB的中点N,连接MN,AN,则MN∥SB.由于AM⊥SB,所以AM⊥MN.由正三棱锥的性质易知SB⊥AC,结合AM⊥SB知SB⊥平面SAC,所以SB⊥SA,SB⊥SC.又正三棱锥的三个侧面是全等的三角形,所以SA⊥SC,所以正三棱锥S-ABC为正方体的一个角,所以正三棱锥S-ABC的外接球即为正方体的外接球.由AB=2,得SA=SB=SC=2,所以正方体的体对角线为2,所以所求外接球的半径R=,其表面积为4πR2=12π,故选B.
12.[2016·商丘二模]设函数f(x)的导函数为f′(x),对任意x∈R都有f(x)>f′(x)成立,则( )
A.3f(ln 2)<2f(ln 3)
B.3f(ln 2)=2f(ln 3)
C.3f(ln 2)>2f(ln 3)
D.3f(ln 2)与2f(ln 3)的大小不确定
答案 C
解析 构造新函数g(x)=,则求导函数得:g′(x)=,因为对任意x∈R,都有f(x)>f′(x),所以g′(x)<0,即g(x)在实数域上单调递减,所以g(ln 2)>g(ln 3),即>,解得3f(ln 2)>2f(ln 3),故本题正确答案为C.
二、填空题
13.若向量a,b满足:|a|=1,|b|=2,(a-b)⊥a,则a,b的夹角是________.
答案
解析 依题意得(a-b)·a=0,即a2-a·b=0,1-2cos〈a,b〉=0,cos〈a,b〉=;又〈a,b〉∈[0,π],因此〈a,b〉=,即向量a
,b的夹角为.
14.若不等式x2+y2≤2所表示的平面区域为M,不等式组表示的平面区域为N,现随机向区域N内抛一粒豆子,则豆子落在区域M内的概率为________.
答案
解析 作出不等式组与不等式表示的可行域如图所示,平面区域N的面积为×3×(6+2)=12,区域M在区域N内的面积为π()2=,故所求概率P==.
15.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,bcosC+ccosB=R(R为△ABC外接圆半径)且a=2,b+c=4,则△ABC的面积为________.
答案
解析 因为bcosC+ccosB=R,
得2sinBcosC+2sinCcosB=,
sin(B+C)=,即sinA=.
由余弦定理得:a2=b2+c2-2bccosA,
即4=b2+c2-bc,∴4=(b+c)2-3bc,
∵b+c=4,∴bc=4,∴S△ABC=bcsinA=.
16.存在实数φ,使得圆面x2+y2≤4恰好覆盖函数y=sin图象的最高或最低点共三个,则正数k的取值范围是________.
答案
解析 当函数y=sin的图象取到最高或最低点时,x+φ=+nπ(n∈Z)⇒x=+kn-φ(n∈Z),由圆面x2+y2≤4覆盖最高或最低点,可知-≤x≤,再令-≤+kn-φ≤,得+-≤n≤+-,分析题意可知存在实数φ,使得不等式+-≤n≤+-的整数解有且只有3个,
∴2≤+--<4⇒0},则A∪B
=( )
A.(-∞,-4)∪[-2,+∞)
B.(2,3]
C.(-∞,3]∪(4,+∞)
D.[-2,2)
答案 A
解析 因为B={x|x>2或x<-4},所以A∪B={x|x<-4或x≥-2},故选A.
3.设x,y∈R,则“x≥1且y≥1”是“x2+y2≥2”的( )
A.既不充分又不必要条件 B.必要不充分条件
C.充要条件 D.充分不必要条件
答案 D
解析 当x≥1,y≥1时,x2≥1,y2≥1,所以x2+y2≥2;而当x=-2,y=-4时,x2+y2≥2仍成立,所以“x≥1且y≥1”是“x2+y2≥2”的充分不必要条件,故选D.
4.据我国西部各省(区,市)2013年人均地区生产总值(单位:千元)绘制的频率分布直方图如图所示,则人均地区生产总值在区间[28,38)上的频率是( )
A.0.3 B.0.4
C.0.5 D.0.7
答案 A
解析 依题意,由题图可估计人均地区生产总值在区间[28,38)上的频率是1-(0.08+0.06)×5=0.3,选A.
5. 如图,在三棱锥P-ABC中,不能证明AP⊥BC的条件是( )
A.AP⊥PB,AP⊥PC
B.AP⊥PB,BC⊥PB
C.平面BPC⊥平面APC,BC⊥PC
D.AP⊥平面PBC
答案 B
解析 A中,因为AP⊥PB,AP⊥PC,PB∩PC=P,所以AP⊥平面PBC,又BC⊂平面PBC,所以AP⊥BC,故A正确;C中,因为平面BPC⊥平面APC,BC⊥PC,所以BC⊥平面APC,AP⊂平面APC,所以AP⊥BC,故C正确;D中,由A知D正确;B中条件不能判断出AP⊥BC,故选B.
6.执行如下程序框图,则输出结果为( )
A.2 B.3
C.4 D.5
答案 C
解析 依次执行框图中的语句:n=1,S=0,T=20;T=10,S
=1,n=2;T=5,S=3,n=3;T=,S=6,n=4,跳出循环,输出的n=4,故选C.
7.已知α∈,tan=,那么sin2α+cos2α的值为( )
A.- B.
C.- D.
答案 A
解析 由tan=,知=,
∴tan2α=-.∵2α∈,∴sin2α=,cos2α=-.
∴sin2α+cos2α=-,故选A.
8.甲、乙两个几何体的正视图和侧视图相同,俯视图不同,如图所示,记甲的体积为V甲,乙的体积为V乙,则( )
A.V甲V乙 D.V甲、V乙大小不能确定
答案 C
解析 由三视图知,甲几何体是一个以俯视图为底面的四棱锥,乙几何体是在甲几何体的基础上去掉一个角,即去掉一个三个面是直角三角形的三棱锥后得到的一个三棱锥,所以V甲>V乙,故选C.
9.[2016·江西南昌调研]设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是( )
A., B.,
C., D.,
答案 A
解析 因为a,b是方程x2+x+c=0的两个实根,所以ab=c,a+b=-1.又直线x+y+a=0,x+y+b=0的距离d=,所以d2=2===-2c,因为0≤c≤,所以-2×≤-2c≤-2×0,得≤-2c≤,所以≤d≤,故选A.
10.[2016·郑州质检]已知函数f(x)=x+,g(x)=2x+a,若∀x1∈,∃x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
A.a≤1 B.a≥1
C.a≤2 D.a≥2
答案 A
解析 由题意知f(x)min≥g(x)min(x∈[2,3]),因为f(x)min=5,g(x)min=4+a,所以5≥4+a,即a≤1,故选A.
11.已知椭圆+=1(a>b>0)的左焦点F(-c,0)关于直线bx+cy
=0的对称点P在椭圆上,则椭圆的离心率是( )
A. B.
C. D.
答案 D
解析 设焦点F(-c,0)关于直线bx+cy=0的对称点为P(m,n),
则所以
所以m===(1-2e2)c,
n===2be2.
因为点P(m,n)在椭圆上,所以+=1,即(1-2e2)2e2+4e4=1,即4e6+e2-1=0,将各选项代入知e=符合,故选D.
12.[2016·武昌调研]已知函数f(x)=sinx-xcosx.现有下列结论:
①∀x∈[0,π],f(x)≥0;
②若0,即<,所以②正确;
当x>0时,“>a”等价于“sinx-ax>0”,
令g(x)=sinx-cx,则g′(x)=cosx-c,
当c≤0时,g(x)>0对x∈恒成立;
当c≥1时,因为对∀x∈.
g′(x)=cosx-c<0,
所以g(x)在区间上单调递减,
从而,g(x)0,g(x)在(0,x0)上单调递增,且g(x)>g(0)=0;
若x∈时,g′(x0)<0,g(x)在上单调递减,
要使g(x)=sinx-cx>0在上恒成立,
必须使g=sin-c=1-c≥0恒成立,即00对∀x∈恒成立;
当c≥1时,g(x)<0,对∀x∈恒成立,
所以若a<0},则A∩(∁UB)等于( )
A.{x|x≥1} B.{x|1≤x<2}
C.{x|00得-30,b>0)的渐近线相同,且双曲线C2的焦距为4,则b=( )
A.2 B.4
C.6 D.8
答案 B
解析 由题意得,=2⇒b=2a,C2的焦距2c=4⇒c==2⇒b=4,故选B.
6.运行下面的程序,如果输出的S=,那么判断框内是( )
A.k≤2013? B.k≤2014?
C.k≥2013? D.k≥2014?
答案 B
解析 当判断框内是k≤n?时,S=++…+=1-,若S=,则n=2014.
7.[2016·郑州质检]将函数f(x)=sin的图象向右平移个单位后得到函数g(x)的图象,则g(x)具有性质( )
A.最大值为1,图象关于直线x=对称
B.在上单调递减,为奇函数
C.在上单调递增,为偶函数
D.周期为π,图象关于点对称
答案 B
解析 由题意得,g(x)=sin=sin(2x-π)=-sin2x,对于A,最大值为1正确,而g=0,图象不关于直线x=对称,故A错误;对于B,当x∈时,2x∈,满足单调递减,显然g(x)也是奇函数,故B正确;C显然错误;对于D,周期T==π,g=-,故图象不关于点对称,故选B.
8.[2016·重庆测试]某几何体的三视图如图所示,则该几何体的体积为( )
A. B.2
C. D.3
答案 C
解析 依题意,如图所示,题中的几何体是从正三棱柱ABC-A1B1C1中截去一个三棱锥B-A1B1E(其中点E是B1C1的中点)后剩余的部分,其中正三棱柱ABC-A1B1C1的底面是一个边长为2的正三角形、高为3,因此该几何体的体积为×3-××3=,选C.
9.[2016·福建质检]若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为( )
A. B.
C. D.
答案 D
解析 设椭圆的方程为+=1(a>b>0),根据椭圆与正方形的对称性,可画出满足题意的图象,如图所示,因为|OB|=a,所以|OA|=a,所以点A的坐标为,又点A在椭圆上,所以+=1,所以a2=3b2,所以a2=3(a2-c2),所以3c2=2a2,所以椭圆的离心率e==,故选D.
10.[2016·河南八市质检]已知a>0,x,y满足约束条件若z=3x+2y的最小值为1,则a=( )
A. B.
C. D.1
答案 B
解析 根据约束条件画出可行域,将z=3x+2y的最小值转化为在y轴上的截距,当直线z=3x+2y经过点B时,z最小,又B点坐标为(1,-2a),代入3x+2y=1,得3-4a=1,得a=,故选B.
11.已知在△ABC中,角A,B,C所对的边分别为a,b,c
,若b=a,C=,S△ABC=sin2A,则S△ABC=( )
A. B.
C. D.2
答案 A
解析 解法一:由b=a,C=,得S△ABC=absinC=a·a·=a2,又S△ABC=sin2A,则=sin2A,故=sinA,即=2,由=,得=2,所以c=2sinC=1,由余弦定理a2+b2-c2=2abcosC,得a2+3a2-1=2·a·a·,整理得4a2-1=3a2,a2=1,所以a=1,故S△ABC=.
解法二:由余弦定理a2+b2-c2=2abcosC,得a2+(a)2-c2=2a·a·cos,即a2=c2,故a=c,从而有A=C=,所以S△ABC=sin2A=×sin2=,故选A.
12.若P为曲线y=ln x上一动点,Q为直线y=x+1上一动点,则|PQ|min等于( )
A.0 B.
C. D.2
答案 C
解析 如图所示,直线l与y=ln x相切且与y=x+1平行时,切点P到直线y=x+1的距离|PQ|即为所求最小值.(ln x)′=,令=1,得x=1.
故P(1,0).故|PQ|min==.
二、填空题
13.[2015·广东高考]已知样本数据x1,x2,…,xn的均值=5,则样本数据2x1+1,2x2+1,…,2xn+1的均值为________.
答案 11
解析 由条件知==5,
则所求均值0=
==2+1=2×5+1=11.
14.已知{an}为等差数列,公差为1,且a5是a3与a11的等比中项,Sn是{an}的前n项和,则S12的值为________.
答案 54
解析 由题意得,a=a3a11,即(a1+4)2=(a1+2)(a1+10),a1=-1,∴S12=12×(-1)+×1=54.
15.设函数f(x)在[1,+∞)上为增函数,f(3)=0,且g(x)=f(x+1)为偶函数,则不等式g(2-2x)<0的解集为________.
答案 (0,2)
解析 依题意得f(-x+1)=f(x+1),因此f(x)的图象关于直线x=1对称.又f(x)在[1,+∞)上为增函数,因此f(x)在(-∞
,1]上为减函数.又g(x)=f(x+1)为偶函数,因此g(x)在[0,+∞)上为增函数,在(-∞,0]上为减函数,且g(2)=f(2+1)=f(3)=0,g(-2)=0,不等式g(2-2x)<0,即g(|2-2x|)0},集合B={x|1-x>0},则A∩B等于( )
A.(1,3) B.(-∞,-1)
C.(-1,3) D.(-1,1)
答案 D
解析 ∵A=(-1,3),B=(-∞,1),∴A∩B=(-1,1).
3.
一次数学考试后,某老师从自己所带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图.已知甲班5名同学成绩的平均数为81,乙班5名同学成绩的中位数为73,则x-y的值为( )
A.2 B.-2
C.3 D.-3
答案 D
解析 由题意得,=81⇒x=0,易知y=3,∴x-y=-3,故选D.
4.已知l,m,n为不同的直线,α,β,γ为不同的平面,则下列判断正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n∥β,α⊥β,则m⊥n
C.若α∩β=l,m∥α,m∥β,则m∥l
D.若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α
答案 C
解析 A项,m,n可能的位置关系为平行,相交,异面,故A错误;B项,根据面面垂直与线面平行的性质可知B错误;C项,根据线面平行的性质可知C正确;D项,若m∥n,根据线面垂直的判定可知D错误,故选C.
5.△ABC的角A,B,C所对的边分别是a,b,c,若cosA=,c-a=2,b=3,,则a=( )
A.2 B.
C.3 D.
答案 A
解析 由余弦定理可知,a2=b2+c2-2bccosA⇒a2=9+(a+2)2-2×3×(a+2)×⇒a=2,故选A.
6.[2016·东北三省联考]如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧视图为( )
答案 D
解析 如图,画出原正方体的侧视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧视图为D.
7.[2016·合肥质检]执行下面的程序框图,则输出的n的值为( )
A.10 B.11
C.1024 D.2048
答案 C
解析 该程序框图共运行10次,S=1+2+22+…+210=2047,输出的n=210=1024,选项C正确.
8.[2016·河南六市一联]实数x,y满足使z=ax+y取得最大值的最优解有2个,则z1=ax+y+1的最小值为( )
A.0 B.-2
C.1 D.-1
答案 A
解析 画出不等式组所表示的可行域如图中阴影部分所示,∵z=ax+y取得最大值的最优解有2个,∴-a=1,a=-1,∴当x=1,y=0或x=0,y=-1时,z=ax+y=-x+y有最小值-1,∴ax+y+1的最小值是0,故选A.
9.已知a,b都是实数,命题p:a+b=2;命题q:直线x+y=0与圆(x-a)2+(y-b)2=2相切,则p是q的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
答案 A
解析 由直线x+y=0与圆(x-a)2+(y-b)2=2相切,得=,即a+b=±2,∴p是q的充分但不必要条件.
10.[2016·山西质检]若函数f(x)=sin(2x+φ)的图象关于直线x=对称,且当x1,x2∈,x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
A. B.
C. D.1
答案 C
解析 由题意得,2×+φ=+kπ,k∈Z,
∴φ=+kπ,k∈Z,∵|φ|<,∴k=0,φ=,
又x1,x2∈,∴2x1+,2x2+∈(0,π),
∴=,解得x1+x2=,
∴f(x1+x2)=sin=,故选C.
11.[2016·云南统检]已知双曲线M的焦点F1、F2在x轴上,直线x+3y=0是双曲线M的一条渐近线,点P在双曲线M上,且·=0,如果抛物线y2=16x的准线经过双曲线M的一个焦点,那么||·||=( )
A.21 B.14
C.7 D.0
答案 B
解析 设双曲线方程为+=1(a>0,b>0),
∵直线x+3y=0是双曲线M的一条渐近线,
∴=①,又抛物线的准线为x=-4,∴c=4②,
又a2+b2=c2③,
∴由①②③得a=3.
设点P为双曲线右支上一点,
∴由双曲线定义得|||-|||=6④,
又·=0,∴⊥,∴在Rt△PF1F2中||2+||2=82⑤,联立④⑤,解得||·||=14.
12.已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log2x-2的零点依次为a,b,c,则( )
A.a0)的焦点为F,其准线与双曲线x2-y2=1相交于A,B两点,若△ABF为等边三角形,则p=________.
答案 2
解析 由题意可知,抛物线的焦点为F,准线方程为y=-,联立解得x=± .
∵△ABF为等边三角形,∴=2|x|,即p2+=4,解得p=2或-2(舍去).
15.[2016·海口调研]半径为2的球O
中有一内接正四棱柱(底面是正方形,侧棱垂直底面).当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是________.
答案 16(π-)
解析 依题意,设球的内接正四棱柱的底面边长为a、高为h,则有16=2a2+h2≥2ah,即4ah≤16,该正四棱柱的侧面积S=4ah≤16,当且仅当h=a=2时取等号.因此,当该正四棱柱的侧面积最大时,球的表面积与该正四棱柱的侧面积之差是4π×22-16=16(π-).
16.已知数列{an}的首项a1=1,前n项和为Sn,且Sn=2Sn-1+1(n≥2,且n∈N*),数列{bn}是等差数列,且b1=a1,b4=a1+a2+a3.设cn=,数列{cn}的前n项和为Tn,则T10=________.
答案
解析 解法一:数列{an}的首项a1=1,前n项和为Sn,且Sn=2Sn-1+1(n≥2,且n∈N*),∴当n=2时,a1+a2=2a1+1,∴a2=2,当n≥3时,an=Sn-Sn-1=2Sn-1-2Sn-2=2an-1,又a2=2a1,∴an=2an-1(n≥2,且n∈N*),数列{an}为首项为1,公比为2的等比数列,∴an=2n-1,a3=22=4.设数列{bn}的公差为d,又b1=a1=1,b4=1+3d=7,∴d=2,bn=1+(n-1)×2=2n-1,cn===,
∴T10=+-+…+-==.
解法二:∵数列{an}的首项a1=1,前n项和为Sn,且Sn=2Sn-1+1(n≥2,且n∈N*),∴当n=2时,a1+a2=2a1+1,∴a2=2,当n=3时,a1+a2+a3=2a1+2a2+1,
∴a3=4.设数列{bn}的公差为d,又b1=a1=1,b4=1+3d=7,∴d=2,bn=1+(n-1)×2=2n-1,cn===
,
∴T10===.