- 2021-06-30 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年山东泰安肥城市高一上学期期中考试数学试题
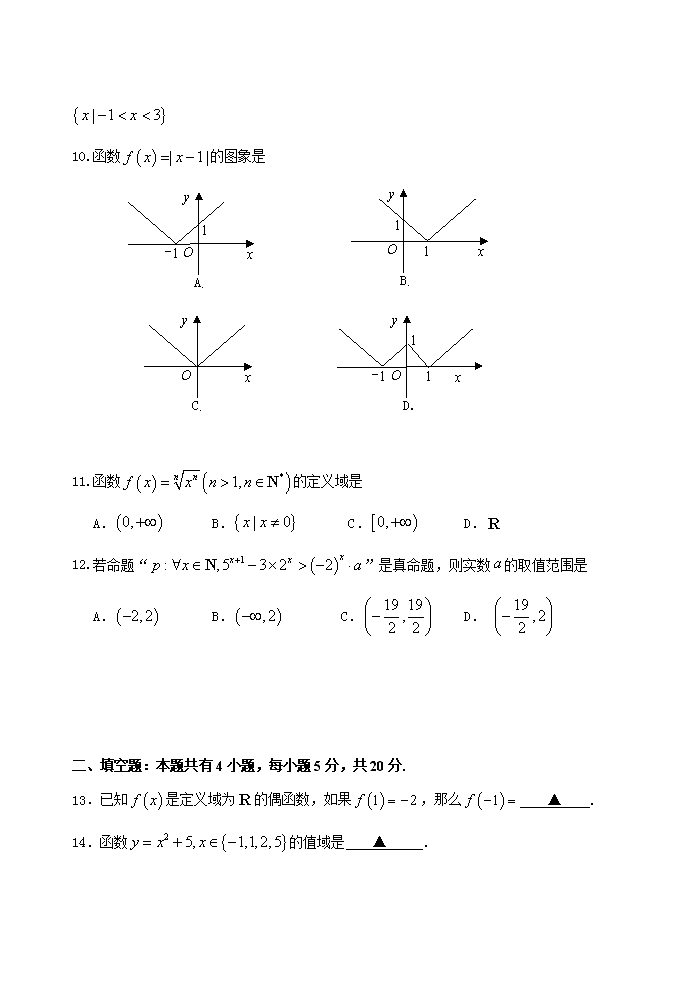
2019-2020学年山东泰安肥城市高一上学期期中考试数学试题 本试卷共22题,满分150分,共6页.考试用时120分钟. 注意事项: 1.答题前,考生先将自己的姓名、准考证号填写在答题卡上. 2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效. 3.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚. 4.保持答题卡卡面清洁,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回. 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集,集合,那么等于 A. B. C. D. 2.存在量词命题的否定是 A. B. C. D. 3.如果,那么的最小值为 A.2 B.3 C.4 D.5 4.中文“函数”(function)一词,最早由近代数学家李善兰翻译.之所以这么翻译,他给 出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个 量的变化而变化.下列选项中两个函数是同一个函数的是 A.与 B.与 C.与 D.与 5.如果幂函数的图象经过点,那么等于 A. B. C. D. 6.函数图象恒过的定点构成的集合是 A. B. C. D. 7.若,且,则下列不等式一定成立的是 A. B. C. D. 8.设,则“”是“”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 9.已知集合,且,则集合可以是 A. B. C. D. 10.函数的图象是 x y O C. 1 A. -1 O x y 1 B. 1 O x y D. 1 1 -1 O x y 11.函数的定义域是 A. B. C. D. 12.若命题“”是真命题,则实数的取值范围是 A. B. C. D. 二、填空题:本题共有4小题,每小题5分,共20分. 13.已知是定义域为的偶函数,如果,那么 ▲ . 14.函数的值域是 ▲ . 15.中国古代十进位制的算筹记数法,在世界数学史上是一个伟大的创造.算筹记数的方法是:个位、百位、万位……的数按纵式的数码摆出;十位、千位、十万位……的数按横式的数码摆出. 1~9这9个数字的纵式与横式表示数码如下图所示: 如138可用算筹表示为,则的运算结果可用算筹表示为 ▲ . 16.已知函数图象上任意两点连线都与轴不平行,则实数的取值范围是 ▲ . 三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤. 17.(10分) 已知集合. (1)当时,写出集合的所有非空子集; (2)若,求的值. 18.(12分) 已知,不等式的解集为. (1)求实数的值; (2)正实数满足,求的最小值. 19.(12分) 已知,函数. (1)用函数单调性的定义证明:在上是增函数; (2)若在上的值域是,求的值. 20.(12分) 信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元? 21.(12分) 关于实数的不等式与 (其中)的解集依次记为与. (1)当时,证明:; (2)若命题是命题的充分条件,求实数的取值范围. 22.(12分) 已知定义在上的偶函数和奇函数,且. (1)求函数,的解析式; (2)设函数, 记. 探究是否存在正整数,使得对任意的,不等式恒成立?若存在,求出所有满足条件的正整数的值;若不存在,请说明理由. 参考结论: 设均为常数,函数的图象关于点对称的充要条件是. 2019—2020学年度上学期高一期中考试 高一数学参考答案及评分标准 一、选择题:每小题5分,共60分. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C A C C A C D A B B D D 二、填空题:每小题5分,共20分. 13. 14. 15. 16.或 三、解答题:共6小题,共70分. 17.(10分) 解:(1)由题意得:,即, ∴. ……………………………………………………………2分 ∴当时,集合. ……………………………………………………3分 ∴的所有非空子集为: ,,,,,,.…………………5分 (本问列举不全不给分,也就是该步骤的2分不得分) (2)∵, ∴,,且,……………………………………9分 ∴. ……………………………………………………………………10分 18.(12分) 解:(1)由题意可知:和是方程的两个根,……………………2分 ∴ ………………………………………………………………4分 解得 ……………………………………………………5分 (2)由题意和(1)可得:,即. ……………………………6分 ∴, ……………………………………7分 ∵,∴. ∴ ………………………………………9分 当且仅当,即,时等号成立. ………………………………11分 ∴的最小值为9. ………………………………………………………12分 19.(12分) 解:(1)由题意可知:. ,且,………………………………………………………1分 则. …………………3分 ∵, ∴, ……………………………………………………………4分 ∴,即, ………………………………………………5分 ∴在上是增函数. …………………………………………………6分 (2)易知,由(1)可知在上为增函数. …………………7分 ∴,解得.…………………………………………………9分 又由,得,解得. ………………………………………12分 20.(12分) 解:设银行裁员人,所获得的经济效益为万元,则 .……………………………5分 由题意:,且, ∴,且. …………………………………………………………8分 ∵函数的对称轴,开口朝下, ∴函数在单调递增,…………………………………9分 ∴当时,取得最大值, ………………………………………………11分 即银行裁员人,所获得的经济效益最大为万元. ………………………12分 21.(12分) 解:∵, ∴.……………………………………………………………1分 又由得, ∴. ………………………………………………2分 (1)当时,,, …3分 ∴对,都有, ∴. ………………………………………………………………………………5分 (2)∵命题是命题的充分条件, ∴. ………………………………………………………………………………6分 当,即时,. 由得,解得.………………………………………9分 当,即时,. 由得,解得. …………………………………………11分 综上可知:的范围是或. …………………………………12分 22.(12分) 解:(1)∵, ∴. …………………………………………………………1分 又为偶函数,为奇函数, ∴ , ……………………………………………………………2分 ∴,. ……………………………………3分 (2)存在满足条件的正整数. ……………………………………………………4分 由题意可知:为奇函数,其图象关于中心对称, ∴函数的图象关于点中心对称, 即对,. ……………………………………………6分 ∵, ∴. 两式相加,得 , 即. ∴. ……………………………………………………………………8分 由, 得,. ∵, ∴, 由此可得恒成立. 即对任意的恒成立. ……………………………………10分 令,,则, ,且, 则 ∵,∴. 则在上单调递增, ∴在上单调递增, ………………………………………11分 ∴ ∴. 又由已知, ∴. ………………………………………………………………………12分查看更多