2018届二轮复习2-7函数的图象课件(全国通用)
2
.
7
函数的图象
-
2
-
-
3
-
知识梳理
考点自测
1
.
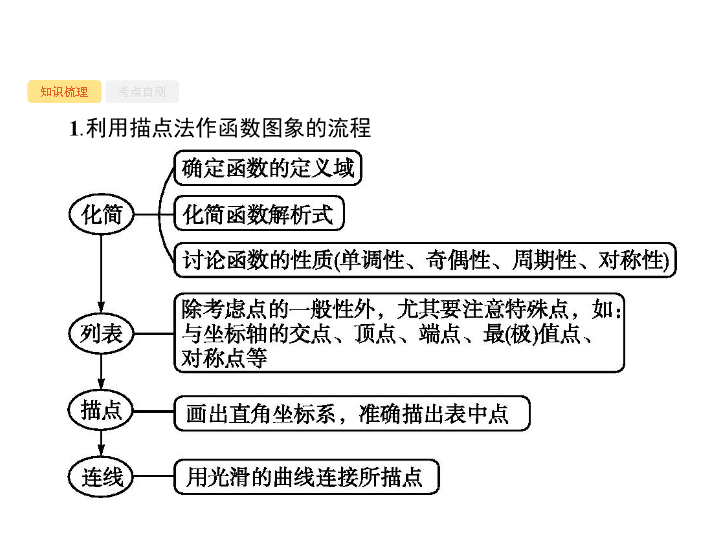
利用描点法作函数图象的流程
-
4
-
知识梳理
考点自测
2
.
函数图象间的变换
(1)
平移变换
对于平移
,
往往容易出错
,
在实际判断中可熟记口诀
:
左加右减
,
上加下减
.
y=
f
(
x
)
-k
-
5
-
知识梳理
考点自测
(2)
对称变换
y=-
f
(
-x
)
的图象
-
6
-
知识梳理
考点自测
-
7
-
知识梳理
考点自测
1
.
判断下列结论是否正确
,
正确的画
“
√
”,
错误的画
“
×
”
.
(1)
将函数
y=
f
(
x
)
的图象先向左平移
1
个单位长度
,
再向下平移
1
个单位长度得到函数
y=f
(
x+
1)
+
1
的图象
.
(
)
(2)
当
x
∈
(0,
+∞
)
时
,
函数
y=|
f
(
x
)
|
与
y=
f
(
|x
|
)
的图象相同
.
(
)
(3)
函数
y=
f
(
x
)
与
y=-
f
(
-x
)
的图象关于原点对称
.
(
)
(4)
若函数
y=
f
(
x
)
满足
f
(1
+x
)
=f
(1
-x
),
则函数
f
(
x
)
的图象关于直线
x=
1
对称
.
(
)
(5)
若函数
y=
f
(
x
)
满足
f
(
x-
1)
=f
(
x+
1),
则函数
f
(
x
)
的图象关于直线
x=
1
对称
.
(
)
×
×
√
√
×
-
8
-
知识梳理
考点自测
2
.
(
教材习题改编
P
24
A
组
T
8
)
如图
,
矩形
ABCD
的周长为
4,
设
AB=x
,
AC=y
,
则
y=
f
(
x
)
的大致图象为
(
)
C
-
9
-
知识梳理
考点自测
D
解析
:
由定义域知
x<
1,
排除
A,B,
且
y=
(1
-x
)
在区间
(
-∞
,1)
上是增函数
,
故选
D
.
-
10
-
知识梳理
考点自测
4
.
(
教材习题改编
P
75
A
组
T
10
)
已知三个函数
①
y=a
x
;
②
y=
log
b
x
;
③
y=
log
c
x
的图象如图所示
,
则
a
,
b
,
c
的大小关系为
(
)
A.
a
1,
c>
1
.
作直线
y=
1
与函数
y=
log
b
x
,
y
=
log
c
x
相交
,
易知
c>b
,
即
a
0,
且
a
≠1)
的图象的关系是
(
)
A.
关于
x
轴对称
B.
关于
y
轴对称
C.
关于直线
x-y
=
0
对称
D.
关于
x+y
=
0
对称
D
-
12
-
知识梳理
考点自测
(
方法二
)
y=
a
x
(
a
>
0,
且
a
≠1)
的图象关于
x
轴对称的解析式为
y=-
a
x
,A
错误
;
关于
y
轴对称的图象的解析式
y=a
-
x
,B
错误
;
关于
x-y
=
0
对称的图象的解析式为
y=
log
a
x
,C
错误
,
故选
D
.
-
13
-
考点一
考点二
考点三
学科素养微专题
考点四
作函数的图象
例
1
作出下列函数的图象
:
(1)
y=|
lg
x|
; (2)
y=
2
x+
2
;
(3)
y=x
2
-
2
|x|-
1; (4)
.
-
14
-
考点一
考点二
考点三
学科素养微专题
考点四
-
15
-
考点一
考点二
考点三
学科素养微专题
考点四
-
16
-
考点一
考点二
考点三
学科素养微专题
考点四
思考
作函数的图象一般有哪些方法
?
解题心得
作函数图象的一般方法
:
(1)
直接法
.
当函数表达式
(
或变形后的表达式
)
是熟悉的基本初等函数时
,
就可根据这些函数的特征直接作出
.
(2)
图象变换法
.
变换包括
:
平移变换、伸缩变换、对称变换、翻折变换
.
(3)
描点法
.
当上面两种方法都失效时
,
则可采用描点法
.
为了通过描少量点
,
就能得到比较准确的图象
,
常常需要结合函数的单调性、奇偶性等性质作出
.
-
17
-
考点一
考点二
考点三
学科素养微专题
考点四
对点训练
1
作出下列函数的图象
:
(1)
y=
10
|
lg
x|
;
(2)
y=|x-
2
|
·(
x+
1);
这是分段函数
,
每段函数的图象可根据正比例函数或反比例函数图象作出
,
如图
.
-
18
-
考点一
考点二
考点三
学科素养微专题
考点四
-
19
-
考点一
考点二
考点三
学科素养微专题
考点四
-
20
-
考点一
考点二
考点三
学科素养微专题
考点四
知式判图、知图判式
(
或判图
)
问题
例
2
(1)(2017
湖北黄冈
3
月模拟
,
文
9)
函数
y=x
5
-x
e
x
的图象大致是
(
)
B
-
21
-
考点一
考点二
考点三
学科素养微专题
考点四
(2)
已知函数
f
(
x
)
的部分图象如图所示
,
则
f
(
x
)
的解析式可以是
(
)
D
-
22
-
考点一
考点二
考点三
学科素养微专题
考点四
(3)
已知定义在区间
[0,2]
上的函数
y=
f
(
x
)
的图象如图所示
,
则
y=-f
(2
-x
)
的图象为
(
)
B
-
23
-
考点一
考点二
考点三
学科素养微专题
考点四
-
24
-
考点一
考点二
考点三
学科素养微专题
考点四
(
方法二
)
当
x=
0
时
,
-f
(2
-x
)
=-f
(2)
=-
1;
当
x=
1
时
,
-f
(2
-x
)
=-f
(1)
=-
1
.
观察各选项
,
可知应选
B
.
-
25
-
考点一
考点二
考点三
学科素养微专题
考点四
思考
已知函数解析式应从哪些方面对函数的图象进行判断辨识
?
解题心得
函数图象的辨识可从以下方面入手
:
(1)
从函数的定义域判断图象
“
左右
”
的位置
;
从函数的值域判断图象的
“
上下
”
位置
.
(2)
从函数的单调性判断图象的变化趋势
.
(3)
从函数的奇偶性判断图象的对称性
.
(4)
从函数的周期性判断图象的循环往复
.
(5)
必要时可求导研究函数性质
,
从函数的特征点
,
排除不合要求的图象
.
利用上述方法
,
可排除、筛选错误与正确的选项
.
-
26
-
考点一
考点二
考点三
学科素养微专题
考点四
对点训练
2
(1)(2017
湖南长沙一模
,
文
10)
函数
y=
ln
|x|-x
2
的图象大致为
(
)
A
-
27
-
考点一
考点二
考点三
学科素养微专题
考点四
(2)(2017
河南三门峡一模
)
已知函数
f
(
x
)
的部分图象如图所示
,
则
f
(
x
)
的解析式可以是
(
)
D
-
28
-
考点一
考点二
考点三
学科素养微专题
考点四
(3)
已知函数
y=
f
(
x
)
和函数
y=
g
(
x
)
的图象
,
则函数
y=
f
(
x
)·
g
(
x
)
的部分图象可能是
(
)
A
-
29
-
考点一
考点二
考点三
学科素养微专题
考点四
解析
:
(1)
令
y=f
(
x
)
=
ln
|x|-x
2
,
其定义域为
(
-∞
,0)
∪
(0,
+∞
),
因为
f
(
-x
)
=
ln
|x|-x
2
=f
(
x
),
所以函数
y=
ln
|x|-x
2
为偶函数
,
其图象关于
y
轴对称
,
故排除
B,D,
当
x
→
+∞
时
,
函数
y<
0,
故排除
C,
故选
A
.
(2)
由题图可知函数是奇函数
,
排除
C;
又
f
(
x
)
=x+
sin
x=
0,
函数只有一个零点
,
所以
A
不正确
;
-
30
-
考点一
考点二
考点三
学科素养微专题
考点四
函数图象的应用
(
多考向
考向
1
利用函数图象确定方程的根的个数
18
-
31
-
考点一
考点二
考点三
学科素养微专题
考点四
显然
x=
0
和
x=
6
为
f
(
x
)
的零点
,
且
f
(
x
)
在
(1,3)
和
(3,5)
内各有一个零点
.
由
f
(1)
>
0,
知
f
(
x
)
在
(0,1)
内存在一个零点
,
同理
f
(
x
)
在
(5,6)
内存在一个零点
.
∴
f
(
x
)
在
[0,6]
上共有
6
个零点
.
∵
函数
g
(
x
)
和
h
(
x
)
的图象关于直线
x=
3
对称
,
∴
f
(
x
)
的零点关于直线
x=
3
对称
,
∴
f
(
x
)
的所有零点之和为
6
×
3
=
18
.
故答案为
18
.
思考
函数图象与方程的根的个数有何关系
?
-
32
-
考点一
考点二
考点三
学科素养微专题
考点四
考向
2
利用函数图象求参数的取值范围
[
-
8,
-
1]
-
33
-
考点一
考点二
考点三
学科素养微专题
考点四
思考
如何根据函数的图象求参数
m
的范围
?
-
34
-
考点一
考点二
考点三
学科素养微专题
考点四
考向
3
利用函数图象求不等式的解集
例
5
如图
,
函数
f
(
x
)
的图象为折线
ACB
,
则不等式
f
(
x
)
≥
log
2
(
x+
1)
的解集是
(
)
A.{
x|-
1
0,
当
x=
0
时
,
y
2
2,
故排除
A,C;
当
x
→
+∞
时
,
y
→
+∞
,
故排除
B,
满足条件的只有
D,
故选
D
.
(3)
特殊值验证法
,
取
x=
2,
则
y=
2
×
4
-
e
2
≈8
-
2
.
718
2
≈0
.
6
∈
(0,1),
排除
A,B;
当
0
查看更多