2020届高考二轮数学解答题题型专练（一）

2020届高考二轮数学解答题题型专练（一）

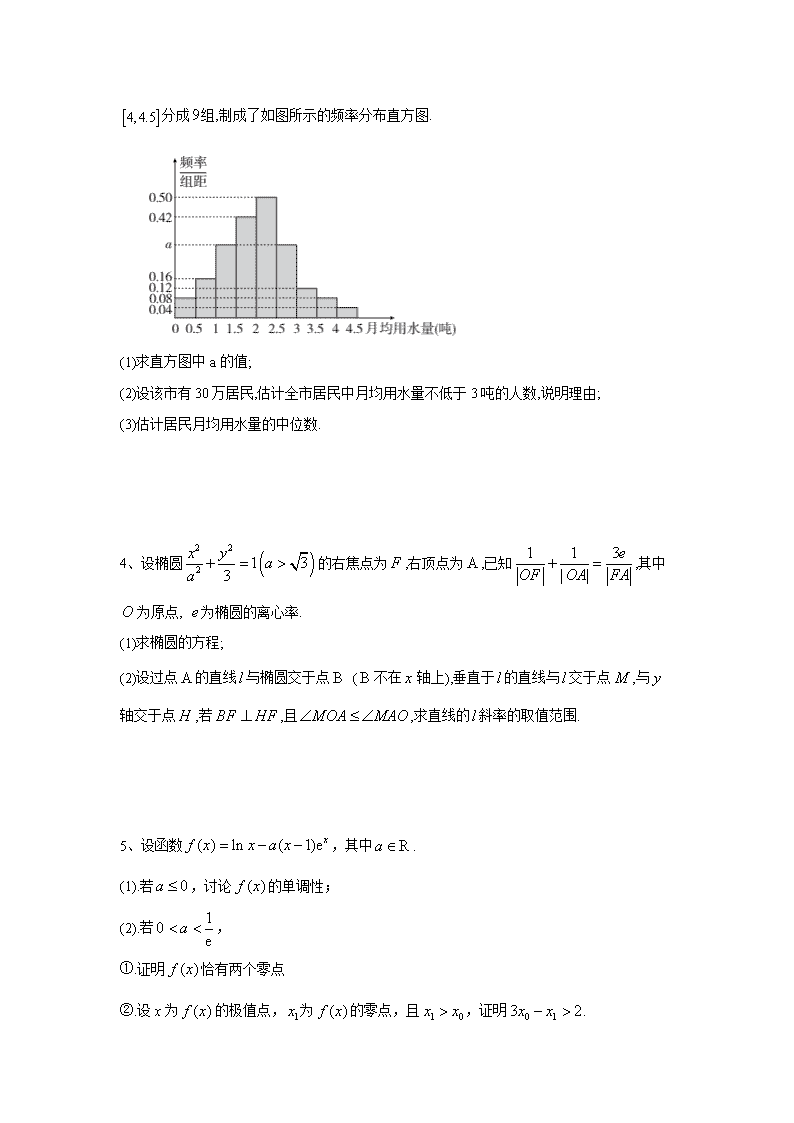
‎2020届高考数学查漏补缺之解答题题型专练（一）‎ ‎1、如图，四边形中，，，设.‎ ‎（1）若面积是面积的4倍，求；‎ ‎（2）若，求.‎ ‎2、如图，四边形是平行四边形，平面平面,, G为的中点.‎ ‎(1)求证：平面；‎ ‎(2)求证：平面平面；‎ ‎(3)求直线与平面所成角的正弦值.‎ ‎3、我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年位居民每人的月均用水量(单位:吨),将数据按照,,,‎ 分成组,制成了如图所示的频率分布直方图. (1)求直方图中a的值; (2)设该市有万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由; (3)估计居民月均用水量的中位数.‎ ‎4、设椭圆的右焦点为,右顶点为,已知,其中为原点, 为椭圆的离心率.‎ ‎(1)求椭圆的方程; (2)设过点的直线与椭圆交于点 (不在轴上),垂直于的直线与交于点,与轴交于点,若,且,求直线的斜率的取值范围.‎ ‎5、设函数，其中.‎ ‎(1).若，讨论的单调性；‎ ‎(2).若，‎ ‎①.证明恰有两个零点 ‎②.设x为的极值点，为的零点，且，证明.‎ ‎ ‎ ‎ ‎ ‎ ‎ 答案以及解析 ‎1答案及解析：‎ 答案：（1）设，则，，， ‎ 由题意，‎ 则， ‎ 所以.∴ ‎ ‎（2）由正弦定理，中，，即①‎ 中，，即②‎ 得：，化简得， ‎ 所以.‎ 解析：‎ ‎ ‎ ‎2答案及解析：‎ 答案：(1)取中点O,连接,在中,因为G是中点,所以且,又因为,,所以且,即四边形是平行四边形，所以,又平面，平面，所以平面.‎ ‎(2)证明：在中,由余弦定理可得，进而得 ‎,即,又因为平面平面平面，平面平面，所以平面.又因为平面，所以，平面平面.‎ ‎(3)因为，所以直线与平面所成的角即为直线与平面所成的角.过点作于点，连接，又平面平面，由(2)知平面，所以直线与平面所成的角即为.在中，，由余弦定理得，所以，因此，，在中,，所以，直线平面所成角的正弦值为.‎ 解析： ‎ ‎ ‎ ‎3答案及解析：‎ 答案：(1)由频率分布直方图可知,月均用水量在的频率为. 同理,在 等组的频率分别为. 由, 解得. (2).由(1)知, 位居民月均用水量不低于吨的频率为 . 由以上样本的频率分布, 可以估计万居民中月均用水量不低于吨的人数为 . (3)设中位数为吨. 因为前组的频率之和为 , 而前组的频率之和为, 所以 ‎. 由,解得. 故可估计居民月均用水量的中位数为吨.‎ 解析：‎ ‎ ‎ ‎4答案及解析：‎ 答案：(1) (2) ‎ 解析：(1)设,由, 即,可得, 又,所以, 因此, 所以椭圆的方程为. (2)设直线的斜率为,则直线的方程为, 设,由方程组,消去, 整理得, 解得或, 由题意得,从而, 由1知,设,有,‎ ‎, 由,得, 所以,解得, 因此直线的方程为, 设,由方程组 消去,得, 在中, , 即,化简得, 即,解得或, 所以直线的斜率的取值范围为.‎ ‎ ‎ ‎5答案及解析：‎ 答案：(1).由已知，的定义域为，且 因此当时，，从而，所以在内单调递增.‎ ‎(2).①由(1)知.令，由，‎ 可知在内单调递减，又，且 ‎.‎ 故在内有唯一解，从而在内有唯一解，不妨设为，‎ 则.当时，，所以在内单调递增；当时，，所以在内单调递减，因此是的唯一极值点.‎ 令，则当时，，故在内单调递减，从而当时，，所以.‎ 从而，‎ 又因为，所以在内有唯一零点.又在内有唯一零点1，从而，在内恰有两个零点.‎ ‎②.由题意，即，从而，即.因为当时，，又，故，两边取对数，得，于是 ‎，‎ 整理得.‎ 解析：‎ ‎ ‎