2018-2019学年黑龙江省大庆第一中学高二寒假开学检测数学（理）试题 Word版

2018-2019学年黑龙江省大庆第一中学高二寒假开学检测数学（理）试题 Word版

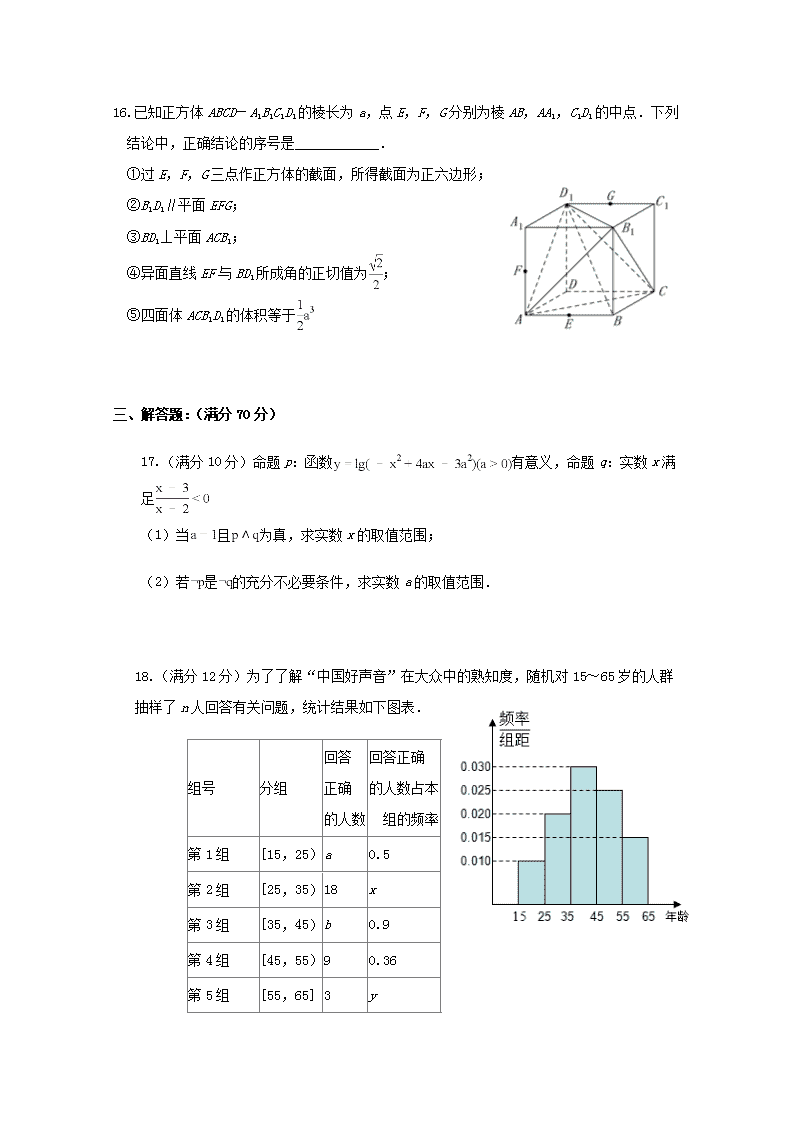
大庆一中2018-2019学年高二年级下学期第一次阶段考试 数学试卷 一、 选择题：(每小题5分满分60分)‎ ‎1. 命题“若a＞b，则a2＞b2”的逆否命题是 ( )‎ A. 若，则 B. 若，则 C. 若，则 D. 若，则 ‎2. “m=-1”是“直线l1：mx+（2m-1）y+1=0与直线l2：3x+my+3=0垂直”的（ ）‎ A. 充分不必要条件B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件 ‎3. 执行如右图所示的程序框图，若输出的S=2，则判断框内可以填入（　　）‎ A. B. C. D. ‎ ‎4. 下列说法正确的是（　　）‎ A. “若，则”的否命题是“若，则” B. “若，则”是真命题 C. ，成立 D. 为等比数列，则“”是“”的既不充分也不必要条件 ‎5. 某校高二某班共有学生60人，现根据座号，用系统抽样的方法，抽取一个容量为5的样本，已知3号，15号，45号，53号同学在样本中，那么样本中还有一个同学座号不能是（ ）‎ A. 26 B. 31 C. 36 D. 37‎ ‎6. 在长方体中，，，则异面直线与所成角的余弦值为（ ）‎ A. B. C. D. ‎ ‎7. 已知变量，之间的线性回归方程为，且变量，之间的一组相关数据如下表所示，则下列说法错误的是（   ）‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎6‎ ‎3‎ ‎2‎ A. 变量x，y之间呈现负相关关系 B. 可以预测，当时， C. D. 由表格数据知，该回归直线必过点 ‎8.设不等式组，表示的平面区域为Ω，在区域Ω内任取一点P(x,y)，则P点的坐标满足不等式的概率为 ( )‎ A. B. C. D. ‎ ‎9. 正四棱锥S-ABCD的侧棱长为，底边长为，E是SA的中点，则异面直线BE和SC所成的角等于（ ）‎ A. ‎ B. C. D. ‎ ‎10．P为双曲线右支上一点，F1，F2分别为双曲线的左、右焦点，且，直线PF2交y轴于点A，则△AF1P的内切圆半径为（　　）‎ A. 2 B. 3 C. D. ‎ ‎11. 己知抛物线y2＝2px（p＞0）的焦点为F，过点F作互相垂直的两直线AB，CD与抛物线分别相交于A，B以及C，D若，则四边形ACBD的面积的最小值为（     ）‎ A. 32 B. 30 C. 18 D. 36‎ ‎12. 已知椭圆，与双曲线具有相同焦点、，且在第一象限交于点P，椭圆与双曲线的离心率分别为、，若，则的最小值是    ‎ A. B. C. D. ‎ 二．填空题：（每小题5分满分20分）‎ ‎13.将一颗质地均匀的骰子先后抛掷2次，则出现向上点数之和小于10的概率是_____________．‎ ‎14.已知样本7，5，，3，4的平均数是5，则此样本的方差为        ‎ ‎15.已知抛物线C：y2=2px（p＞0）的焦点为F，过F且倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点，与它的准线交于点P，则= ______ ．‎ ‎16.已知正方体ABCD－A1B1C1D1的棱长为a，点E，F，G分别为棱AB，AA1，C1D1的中点．下列结论中，正确结论的序号是____________． ①过E，F，G三点作正方体的截面，所得截面为正六边形； ②B1D1∥平面EFG； ③BD1⊥平面ACB1； ④异面直线EF与BD1所成角的正切值为； ⑤四面体ACB1D1的体积等于 三、解答题：（满分70分）‎ ‎17.（满分10分）命题p：函数有意义，命题q：实数x满足 （1）当且为真，求实数x的取值范围；‎ ‎（2）若是的充分不必要条件，求实数a的取值范围．‎ ‎18.（满分12分）为了了解“中国好声音”在大众中的熟知度，随机对15～65岁的人群抽样了n人回答有关问题，统计结果如下图表．‎ 组号 分组 回答 正确 的人数 回答正确 的人数占本 组的频率 第1组 ‎[15，25）‎ a ‎0.5‎ 第2组 ‎[25，35）‎ ‎18‎ x 第3组 ‎[35，45）‎ b ‎0.9‎ 第4组 ‎[45，55）‎ ‎9‎ ‎0.36‎ 第5组 ‎[55，65]‎ ‎3‎ y ‎（1）分别求出a，b，x，y的值；‎ ‎（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．‎ ‎19.（满分12分）如图，在多面体ABCDEF中，ABCD是正方形，平面ABCD，平面ABCD，，点M为棱AE的中点． 求证：平面平面EFC；‎ 若，求直线AE与平面BDM所成的角的正弦值．‎ ‎20.（满分12分）抛物线Q：，焦点为F． 若是抛物线内一点，P是抛物线上任意一点，求的最小值； 过F的两条直线，，分别与抛物线交于A、B和C、D四个点，记M、N 分别是线段AB、CD的中点，若，证明：直线MN过定点，并求出这个定点坐标．‎ ‎21.（满分12分）如图，四棱锥P-ABCD的底面ABCD是平行四边形，∠BAC=∠PAD=∠PCD=90°．‎ ‎（1）求证：平面PAB⊥平面ABCD；‎ ‎（2）若AB=AC=PA=3，E为BC的中点，F为棱PB上的点，PD∥平面AEF，求二面角A-DF-E的余弦值 ‎22.（满分12分）已知椭圆C：=1（a＞b＞0）的离心率为，以椭圆长、短轴四个端点为顶点的四边形的面积为4． （1）求椭圆C的方程； （2）如图所示，记椭圆的左、右顶点分别为A、B，当动点M在定直线x=4上运动时，直线AM、BM分别交椭圆于P、Q两点，求四边形APBQ面积的最大值．‎ 大庆一中高二年级下学期第一次阶段考试 数学答案 一、选择题：‎ CACB DACA DBAD 二、填空题：‎ ‎13. 14.2 15. 16. ①③④‎ 三、解答题：‎ ‎17.解：（1）由-x2+4ax-3a2＞0得x2-4ax+3a2＜0，即（x-a）（x-3a）＜0，其中a＞0， 得a＜x＜3a，a＞0，则p：a＜x＜3a，a＞0． 若a=1，则p：1＜x＜3，由解得2＜x＜3．即q：2＜x＜3． 若p∧q为真，则p，q同时为真，即，解得2＜x＜3， ∴实数x的取值范围（2，3）． （2）若￢p是￢q的充分不必要条件，即q是p的充分不必要条件， ∴即（2，3）是（a，3a）的真子集． 所以，解得1≤a≤2．实数a的取值范围为[1，2]．‎ ‎18.解：（Ⅰ）由频率表中第4组数据可知，第4组总人数为， 再结合频率分布直方图可知n=， ∴a=100×0.01×10×0.5=5，b=100×0.03×10×0.9=27，…‎ ‎（Ⅱ）因为第2，3，4组回答正确的人数共有54人， 所以利用分层抽样在54人中抽取6人，每组分别抽取的人数为：第2组：人；第3组：人；第4组：人 设第2组2人为：A1，A2；第3组3人为：B1，B2，B3；第4组1人为：C1． 则从6人中随机抽取2人的所有可能的结果为：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C1）， （A2，B1），（A2，B2），（A2，B3），（A2，C1），（B1，B2），（B1，B3），（B1，C1），‎ ‎（B2，B3），（B2，C1），（B3，C1）共15个基本事件，其中恰好没有第3组人共3个基本事件， ∴所抽取的人中恰好没有第3组人的概率是：．‎ ‎19.证明：连结AC，交BD于点N， 为AC的中点，． 平面EFC，平面EFC， 平面EFC． ，DE都垂直底面ABCD， ． ，为平行四边形， 平面EFC，平面EFC， 平面EFC． 又， 平面平面EFC． 解：由已知，平面ABCD，是正方形． 两两垂直，如图，建立空间直角坐标系． 设，则，从而， ， 设平面的一个法向量为， 由得． 令，则，从而． ， 设与平面所成的角为，则， 所以，直线与平面所成角的正弦值为．‎ ‎20.解：由抛物线定义知，等于P到准线的距离， 的最小值即为点E到准线的距离，等于4． ‎ 证明：由，得：，解得，代入，得， 同理，， ， ：， 变形得：， 因为，所以进一步化简得， 所以MN恒过定点．‎ ‎21.解：（1）证明：∵AB∥CD，PC⊥CD，∴AB⊥PC， ∵AB⊥AC，AC∩PC=C，∴AB⊥平面PAC， ∴AB⊥PA，又∵PA⊥AD，AB∩AD=A， ∴PA⊥平面ABCD，PA⊂平面PAB， ∴平面PAB⊥平面ABCD； （2）连接BD交AE于点O，连接OF， ∵E为BC的中点，BC∥AD，∴==， ∵PD∥平面AEF，PD⊂平面PBD， 平面AEF∩平面PBD=OF， ∴PD∥OF，∴==， 以AB，AC，AP所在直线分别为x轴，y轴，z轴建立空间直角坐标系A-xyz， 则A（0，0，0），B（3，0，0），C（0，3，0），D（-3，3，0）， P（0，0，3），E（，，0），F（2，0，1）， 设平面ADF的法向量m=（x1，y1，z1）， ∵=（2，0，1），=（-3，3，0）， 由•m=0，•m=0得取m=（1，1，-2）． 设平面DEF的法向量n=（x2，y2，z2）， ‎ ‎∵=（，-，0），=（，-，1）， 由•n=0，•n=0得取n=（1，3，4）． cos⟨m，n＞==-， ∵二面角A-DF-E为钝二面角，∴二面角A-DF-E的余弦值为-． 22.解：（Ⅰ）根据题意，椭圆C：=1（a＞b＞0）的离心率为，则有a=2c， 以椭圆长、短轴四个端点为顶点的四边形的面积为4，则有2ab=4， 又a2=b2+c2，解得a=2，b=，c=1， 故椭圆C的方程为+=1； （Ⅱ）由于对称性，可令点M（4，t），其中t＞0． 将直线AM的方程y=（x+2）代入椭圆方程+=1，得 （27+t2）x2+4t2x+4t2-108=0， 由xA•xP=，xA=-2得xP=-，则yP=． 再将直线BM的方程y=（x-2）代入椭圆方程+=1得 （3+t2）x2-4t2x+4t2-12=0， 由xB•xQ=，xB=2得xQ=，则yQ=． 故四边形APBQ的面积为S=|AB||yP-yQ|=2|yP-yQ|=2（+）===． 由于λ=≥6，且λ+在[6，+∞）上单调递增，故λ+≥8， 从而，有S=≤6．当且仅当λ=6，即t=3，也就是点M的坐标为（4，3）时，四边形APBQ 的面积取最大值6． ‎