福建省福州市福建师大附中2019-2020学年高一上学期期中考试数学试题
福建师大附中 2019-2020 学年上学期期中考试卷
高一数学·必修 1
一、选择题(每小题 5 分,共 60 分;在给出的 A,B,C,D 四个选项中,只有一项符合题目要求)
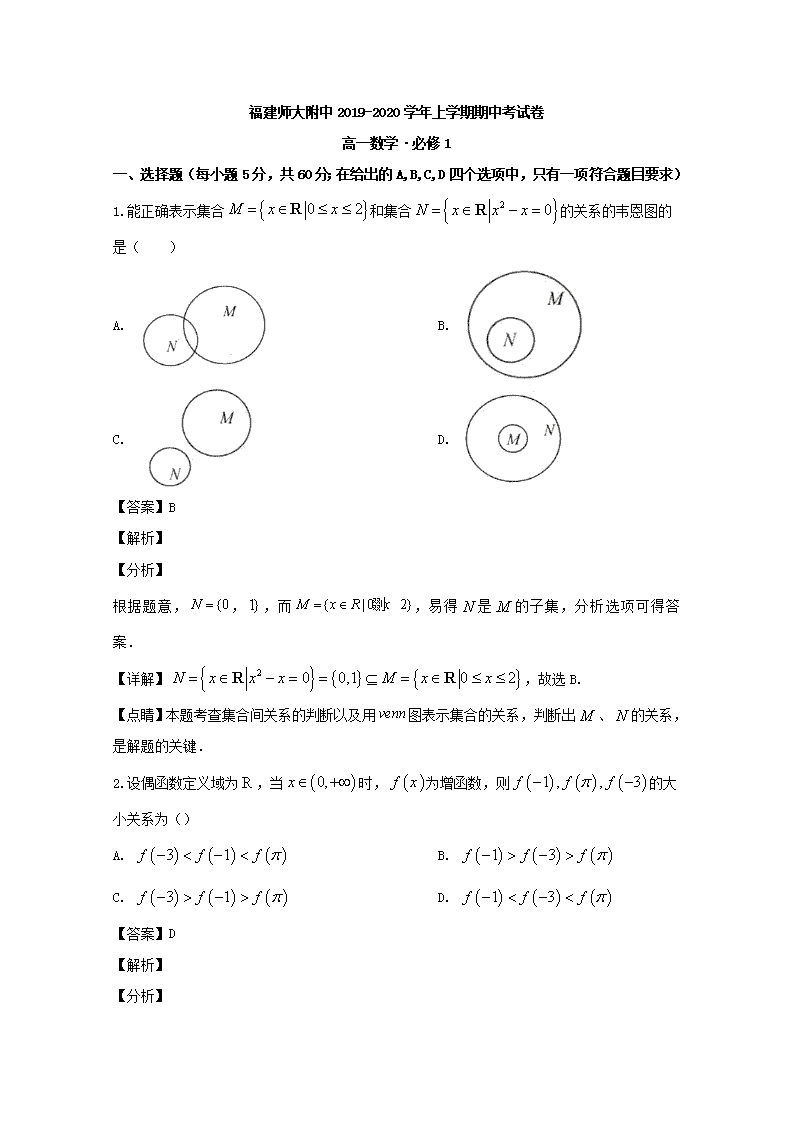
1.能正确表示集合 和集合 的关系的韦恩图的
是( )
A. B.
C. D.
【答案】B
【解析】
【分析】
根据题意, , ,而 ,易得 是 的子集,分析选项可得答
案.
【详解】 ,故选 B.
【点睛】本题考查集合间关系的判断以及用 图表示集合的关系,判断出 、 的关系,
是解题的关键.
2.设偶函数定义域为 ,当 时, 为增函数,则 的大
小关系为()
A. B.
C. D.
【答案】D
【解析】
【分析】
{ }0 2M x x= ∈ ≤ ≤R { }2 0N x x x= ∈ − =R
{0N = 1} { | 0 2}M x R x= ∈ N M
{ } { } { }2 0 0,1 0 2N x x x M x x= ∈ − = = ⊆ = ∈ ≤ ≤R R
venn M N
R ( )0,x∈ +∞ ( )f x ( ) ( ) ( )1 , , 3f f fπ− −
( ) ( ) ( )3 1f f f π− < − < ( ) ( ) ( )1 3f f f π− > − >
( ) ( ) ( )3 1f f f π− > − > ( ) ( ) ( )1 3f f f π− < − <
由于 为偶函数且当 时, 为增函数,故将 全部利
用偶函数性质转换到 上再用单调性进行求解。
【详解】因为 为偶函数,故 ,又因为当 时,
为增函数,故 ,故 ,故选 D。
【点睛】根据奇偶性与单调性求解函数大小关系时,可以将自变量的值转换到同一单调区间
上进行分析。
3.设全集为 R,集合 , ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】
解出集合 、 ,再利用补集和交集的定义可得出集合 .
【详解】由 , , .
由 ,得 或 ,则 , ,
因此, ,故选:B.
【点睛】本题考查交集和补集的混合运算,同时也考查了对数不等式以及函数定义域的求解,
考查计算能力,属于中等题.
4.下列四组中, 与 表示同一函数的是( )
A. , B. ,
C. , D. ,
【答案】D
【解析】
【分析】
( )f x ( )0,x∈ +∞ ( )f x ( ) ( ) ( )1 , , 3f f fπ− −
( )0,x∈ +∞
( )f x ( ) ( ) ( ) ( )1 = 1 , 3 = 3f f f f− − ( )0,x∈ +∞
( )f x ( ) ( ) ( )1 3f f f π< < ( ) ( ) ( )1 3f f f π− < − <
{ }2log 1A x x= < { }2 1B x y x= = − ( )RA B =
{ }0 2x x< < { }0 1x x< < { }1 1x x− < <
{ }1 2x x− < <
A B ( )RA B
2log 1x < 0 2x< < { }0 2A x x∴ = < <
2 1 0x − ≥ 1x ≤ − 1x ≥ { }1 1B x x x= ≤ − ≥或 { }1 1R B x x∴ = − < <
( ) { }0 1A B x x∩ = <
2 21 1 01 1 1
− < − =+ +xe
2( ) 1 01
= − < + xf x x e
0x < 2 21 1 01 1 1
− > − =+ +xe
2( ) 1 01
= − < + xf x x e
( )5 21y x xx
= + ≥+ x
5 1− 2 5 5 1+
( )51 1 21y x xx
= + + − ≥+
( )5 51 1 21 1y x x xx x
= + = + + − ≥+ +
1 ( 3)x t t+ = ≥
5( ) 1f t t t
= + − ( 5, )+∞
min( ) (3)f t f=
3t = 2x =
( )y f x= 33, 3
2
1log 2f f
=
A. B. C. D.
【答案】B
【解析】
【分析】
设 ,将点 的坐标代入函数 的解析式,求出 的值,然后再计算
出 的值.
【详解】设 ,由题意可的 ,即 , ,则 ,
所以, ,
因此, ,故选:B.
【点睛】本题考查指数幂的计算,同时也考查了对数运算,解题的关键就是求出幂函数的解
析式,同时利用指数幂的运算性质进行计算,考查计算能力,属于中等题.
8.对于一个声强为 为(单位: )的声波,其声强级 (单位: )可由如下公式计
算: (其中 是能引起听觉的最弱声强),设声强为 时的声强级为 70 ,声
强为 时的声强级为 60 ,则 是 的( )倍
A. 10 B. C. D.
【答案】A
【解析】
【分析】
根据声强级与声强之间的关系式,将两个声强级作差,结合对数的运算律可得出 的值,可
得出答案。
2
2 2 2− 1
2
( ) af x x= 33, 3
( )y f x= a
2
1log 2f f
( ) af x x= ( ) 33 3 3
af = = 1
23 3a −=
1
2a∴ = − ( ) 1
2f x x
−=
1
12
21 1 22 2f
− = =
1
1 12
2 2
2 2
1 1 1log log 2 2 22 2 2f f f f
− = = = = =
I 2/W m L dB
0
10lg IL I
=
0I 1I dB
2I dB 1I 2I
100 1010 10000
1
2
I
I
【详解】由题意可得 ,即 ,两式相减得 ,所以, ,
因此, 是 的 倍,故选:A.
【点睛】本题考查对数的运算律,考查对数在实际问题的应用,熟练应用对数的运算性质是
解本题的关键,其次就是要弄清题目的意思,考查理解能力与运算能力,属于中等题。
9.已知 , 分别是定义在 上的偶函数和奇函数,若 ,则
A. B. C. D.
【答案】A
【解析】
【分析】
根据奇偶性可得 ,构造方程组求得 解析式,代入 即可求得结
果.
【详解】 分别为 上的偶函数和奇函数
又
本题正确选项:
【点睛】本题考查函数值的求解问题,涉及到构造函数法求解函数解析式、函数奇偶性的应
用等知识.
10.若函数 且 )在区间(0,2)上为减函数,则实数 的取值
范围为( )
A. 0< <1 B. 1< <2 C. 1< ≤2 D. ≤ <1
【答案】C
【解析】
1
0
2
0
10lg 70
10lg 60
I
I
I
I
=
=
1
0
2
0
lg 7
lg 6
I
I
I
I
=
=
1
2
lg 1I
I
= 1
2
10I
I
=
1I 2I 10
( )f x ( )g x R ( ) ( ) 12xf x g x ++ =
( )1g − =
3
2
− 3
2
5
2
5
2
−
( ) ( ) 12 xf x g x − +− = ( )g x 1x = −
( ) ( ),f x g x R
( ) ( ) ( ) ( ) 12 xf x g x f x g x − +∴ − + − = − =
( ) ( ) 12xf x g x ++ = ( ) ( )1 11 2 22
x xg x + − +∴ = − ( ) ( )1 31 1 42 2g∴ − = × − = −
A
( ) log (4 )( 0af x ax a= − > 1a ≠ a
a a a 1
2
a
【分析】
根据复合函数的单调性以及对数函数的定义域列不等式组,解不等式组求得 的取值范围.
【详解】注意到 为定义域上的的减函数,根据复合函数单调性同增异减可知 ,
根据对数函数的定义域有 ,解得 .
故选 C.
【点睛】本小题主要考查已知对数型复合函数单调性求参数,考查对数函数的定义域,属于
中档题.
11.某地一天内的气温 (单位: )与时刻 (单位: )之间的关系如图所示,令
表示时间段 内的温差(即时间段内最高温度与最低温度的差),则 与 之间的函数
图像大致是( )
A. B.
C. D.
a
4y ax= − 1a >
1
4 2 0
a
a
>
− ≥ 1 2a< ≤
( )Q t ℃ t h ( )C t
[ ]0,t ( )C t t
【答案】D
【解析】
【分析】
根据题意,分析函数图像的特征,可得函数 过原点,在 上,
不断增大,在 上, 先是一个定值,然后增大,在 上, 是个定值,分
析选项可得答案。
【详解】由题图看出, 时, ,排除 B;在 上, 不断增大,在
上, 先是一个定值,然后增大,在 上, 不断增大,在 上, 是
个定值,在 上, 不断增大,
故选 D.
【点睛】本题考查函数图像与图像的变化,属于基础题。
12.太极图是由黑白两个鱼形纹组成的图案,太极图展现了一种相互转化,相互统一的和谐美.
定义:能够将圆 的周长和面积同时等分成两部分的函数称为圆 的一个“太极函数”.下列
有关说法中正确的个数是( )个
①对圆 的所有非常数函数的太极函数中,一定不能为偶函数;
②函数 是圆 的一个太极函数;
③存在圆 ,使得 是圆 的太极函数;
④直线 所对应的函数一定是圆
的太极函数.
A. B. C. D.
【答案】B
【解析】
( )C t [ ] [ ] [ ]0,4 , 8,12 , 20,24 ( )C t
[ ]4,8 ( )C t [ ]12,20 ( )C t
0t = ( ) 0C t = [ ]0,4 ( )C t [ ]4,8
( )C t [ ]812, ( )C t [ ]12 20, ( )C t
[ ]20,24 ( )C t
O O
2 2: 1O x y+ =
( ) 1f x x= + ( )22: 1 1O x y+ − =
O ( ) 1
1
x
x
ef x e
+= − O
( ) ( )1 2 1 1 0m x m y+ − + − =
( ) ( ) ( )2 2 2: 2 1 0O x y R R− + − = >
1 2 3 4
【分析】
利用“太极函数”的定义逐个判断函数是否满足新定义即可.
【详解】对于①,如下图所示,若太极函数为偶函数,该函数平分圆 的周长和面积,①错
误;
对于②,函数 的图象是过圆 圆心的一条直线,平分圆 的周
长和面积,②正确;
对于③, ,定义域为 ,关于原点对称.
,该函数为奇函数.
当 时, ,当 时, ,此时函数
单调递减.
当 时, ,当 时, ,此时函数
单调递减.
函数 的图象关于原点对称,有三条渐近线 , .
可知函数 对称中心为间断点,故不存在圆 使得函数 满足题
干条件,③错误;
对于④,对于直线 的方程,变形为 ,
令 ,得 ,直线 经过圆 的圆心,可以平分
圆 周长和面积,④正确.
的
O
( ) 1f x x= + ( )22: 1 1O x y+ − = O
( ) ( )1 21 211 1 1
xx
x x x
eef x e e e
− ++= = = +− − −
{ }0x x ≠
( ) ( )
1 11 1
11 11
x xx
x x
x
e eef x f xe e
e
−
−
++ +− = = = = −− −−
( )0 0x x→ > ( )f x → +∞ x → +∞ ( ) ( )1 1f x f x → >
( )y f x=
( )0 0x x→ < ( )f x → −∞ x → −∞ ( ) ( )1 1f x f x → − < −
( )y f x=
( )y f x= 1y = ± 0x =
( ) 1
1
x
x
ef x e
+= − O ( ) 1
1
x
x
ef x e
+= −
( ) ( )1 2 1 1 0m x m y+ − + − = ( ) ( )2 1 0m x y x y− + − − =
2 0
1 0
x y
x y
− =
− − =
2
1
x
y
=
=
( ) ( )1 2 1 1 0m x m y+ − + − = O
O
因此,真命题的序号为②④.
故选:B.
【点睛】本题考查函数对称性的判定与应用,将新定义理解为函数的对称性为解题的关键,
考查推理能力,属于中等题.
二、填空题(每小题 5 分,共 30 分)
13.分解因式: _______________.
【答案】
【解析】
【分析】
对代数式提公因式 ,然后利用十字分解法可将代数式进行分解.
【详解】由题意可得 .
故答案为: .
【点睛】本题考查代数式的因式分解,考查计算能力,属于基础题.
14.已知 ,当 时,其值域是________
【答案】
【解析】
【分析】
令 ,因为 ,所以 ,得到函数 ,利用
二次函数的性质,即可求解,得到答案.
【详解】由题意,令 ,因为 ,所以 ,
则函数 ,
所以当 时,函数 取得最小值,最小值为 ,
当 时,函数 取得最大值,最小值为 ,
所以函数 的值域为 ,
23 5 6x x x− + =
( )( )2 3x x x− −
x
( ) ( )( )3 2 25 6 5 6 2 3x x x x x x x x x− + = − + = − −
( )( )2 3x x x− −
4 3 2 3x xy = − ⋅ + [ ]0,2x∈
3 ,74
2xt = [ ]0,2x∈ [1,4]t ∈ ( ) 2 23 33 3 ( )2 4f t t t t= − + = − +
2xt = [ ]0,2x∈ [1,4]t ∈
( ) 2 23 33 3 ( )2 4f t t t t= − + = − +
3
2t = ( )f t 3 3( )2 4f =
4t = ( )f t (4) 7f =
4 3 2 3x xy = − ⋅ + 3 ,74
故答案为: .
【点睛】本题主要考查了指数函数的性质,以及二次函数的图象与性质的应用,着重考查了
换元思想,以及推理与运算能力,属于基础题.
15.已知 ,试用 表示 ________.
【答案】
【解析】
【分析】
利用换底公式,可得 ,两式相乘可得 ,将所
求换底为 2 计算即可.
【详解】因为 ,
所以 ,
两式相乘可得, ,
.
【点睛】本题主要考查了对数的换底公式,对数的运算性质,属于中档题.
16.设 ,则 ___________.
【答案】
【解析】
分析】
根据函数 的解析式逐步计算出 的值.
【详解】 ,
.
【
3 ,74
2 3log 3 log 7m n= =, m n、 42log 56 =
3
1
mn
mn m
+
+ +
2 3
lg3 lg7log 3 log 7lg 2 lg3m n= = = =, 2log 7 mn=
2 3log 3 log 7m n= =,
2 3
lg3 lg7log 3 log 7lg 2 lg3m n= = = =,
2
lg7 log 7lg 2 mn= =
2 2 2
42
2 2 2 2 2
log 56 log 7 log 8 3 3log 56 log 42 log 6 log 7 1+log 3 log 7 1
mn mn
m mn
+ + += = = =+ + + +
( ) ( )
( ) ( )
2, 10
6 , 10
x x
f x f f x x
− ≥= + <
( )5f =
11
( )y f x= ( )5f
( ) ( )
( ) ( )
2, 10
6 , 10
x x
f x f f x x
− ≥= + <
( ) ( ) ( ) ( ) ( )5 11 9 15 13 11f f f f f f f ∴ = = = = =
故答案为: .
【点睛】本题考查分段函数的函数值计算,解题时要结合自变量所满足的定义域选择合适的
解析式进行计算,考查计算能力,属于中等题.
17.如图,在平面直角坐标系 中,已知曲线 、 、 依次为 ,
, 的图像,其中 为常数, ,点 是曲线 上位于第一象限
的点,过 分别作 轴、 轴的平行线交曲线 分别于点 、 ,过点 作 轴的平行线交
曲线 于点 ,若四边形 为矩形,则 的值是________.
【答案】
【解析】
【分析】
设点 ,其中 ,可求出点 、 的坐标,进一步求出点 的坐标,再将点
的坐标代入函数 的解析式可求出实数 的值.
【 详 解 】 设 点 , 其 中 , 设 点 、 , 则
,
解得 ,所以,点 、 ,则点 的坐标为 ,
将点 的坐标代入函数 的解析式,得 , ,解得 .
故答案为: .
【点睛】本题考查对数的运算,解题的关键就是由点 的坐标计算出点 的坐标,考查计算
能力,属于中等题.
11
xOy 1C 2C 3C 22logy x=
2logy x= 2logy k x= k 0 1k< < A 1C
A x y 2C B D B y
3C C ABCD k
1
2
( )2,2logA t t 1t > B D D D
2logy k x= k
( )2,2logA t t 1t > ( )2,2logB x t ( ),D t y
2 2
2
log 2log
log
x t
y t
=
=
2
2log
x t
y t
=
=
( )2
2,2logB t t ( )2,logD t t D ( )2
2,logt t
D 2logy k x= 2
2 2log logt k t= 2 1k∴ = 1
2k =
1
2
A D
18.若 表示 、 两数中的最大值,若 关于 对称,
则 ____.
【答案】
【解析】
【分析】
由于函数 的图象关于 轴对称,函数 的图象关于直线 对称,可得知函数
的图象关于直线 对称,由此可求出 的值.
【详解】由于函数 的图象关于 轴对称,函数 的图象关于直线 对称,
则函数 的图象关于直线 ,则 ,解得 .
故答案为: .
【点睛】本题考查分段函数的基本性质,考查函数对称性的应用,解题的关键就是确定所求
函数的对称轴方程,考查分析问题和解决问题的能力,属于中等题.
三、解答题(要求写出过程,共 60 分)
19.按要求完成下列各题
(1)求值
(2)已知 ,求 .
【答案】(1) ;(2) .
【解析】
【分析】
(1)利用对数 运算律、指数的运算律、对数的恒等式以及根式的运算性质可得出结果;
(2)在等式 两边平方,可求出 的值,由此可计算出 ,从而得出
的值.
【详解】(1)原式
;
的
{ }max ,a b a b ( ) { }max ,x x tf x e e −= 2019x =
t =
4038
xy e= y x ty e −= x t=
( )y f x= 0
2
tx
+= t
xy e= y x ty e −= x t=
( ) { }max ,x x tf x e e −= 0
2
tx
+= 20192
t = 4038t =
4038
71 log 2
2
2log 2lg5 lg 4 7 3 2 22
−− − + + −
1 3x x−+ = 1x x−−
2 5±
1 3x x−+ = 2 2x x−+ ( )21x x−−
1x x−−
( ) ( )
7
1 2 22
2 log 2
7log 2 2lg5 2lg 2 2 2 2 1 17
−= − + + + − × × +
( )1 72 2 1 22 2
= − − + + − =
(2) , ,则 .
,因此, .
【点睛】本题考查指数幂的化简与计算、对数的运算性质,熟悉指数与对数的运算律是解题
的关键,考查计算能力,属于基础题.
20.已知集合 , .
(1)若 ,求实数 的取值范围;
(2)若 ,求实数 的取值范围.
【答案】(1) ;(2) .
【解析】
【分析】
(1)由题得 解不等式即得解;(2)对集合 A 分两种情况讨论即得实数 的取
值范围.
【详解】(1)若 ,则 解得 .
故实数 的取值范围是 .
(2)①当 时,有 ,解得 ,满足 .
②当 时,有 ,解得
又 ,则有 或 ,解得 或 ,
或 .
综上可知,实数 的取值范围是 .
【点睛】本题主要考查根据集合的关系和运算求参数的范围,意在考查学生对这些知识的理
解掌握水平和分析推理能力.
21.函数 是定义在 上的偶函数,当 时, .
1 3x x−+ = ( )1 2 2 2 9x x x x− −∴ + = + + = 2 2 7x x−+ =
( )1 2 2 2 5x x x x− −∴ − = + − = 1 5x x−− = ±
{ }1 2 1A x a x a= − < < + { }0 1B x x= < <
B A⊆ a
A B = ∅ a
[ ]0,1 [ )1, 2,2
−∞ − +∞
1 0,
2 1 1,
1 2 1,
a
a
a a
−
+
− < +
a
B A⊆
1 0,
2 1 1,
1 2 1,
a
a
a a
−
+
− < +
0 1a≤ ≤
a [ ]0,1
A = ∅ 1 2 1a a− ≥ + 2a ≤ − A B = ∅
A ≠ ∅ 1 2 1a a− < + 2.a > −
A B = ∅ 2 1 0a + ≤ 1 1a − ≥ 1
2a ≤ − 2a ≥
12 2a∴− < ≤ − 2a ≥
a [ )1, 2,2
−∞ − +∞
( )f x R 0x ≥ ( ) 2 2 1f x x x= − −
(1)求 的函数解析式;
(2)作出 的草图,并求出当函数 有 个不同零点时, 的取
值范围.
【答案】(1) ;(2) .
【解析】
【分析】
(1)设 ,计算出 的表达式,再由偶函数的定义得出函数 在 时的
解析式,从而可得出函数 在 上的解析式;
(2)由 ,得出 ,将问题转化为当直线 与函数 的图象有
个交点时,求实数 的取值范围,然后作出函数 的图象,利用数形结合思想可
求出实数 的取值范围.
【详解】(1)当 时, ,则 ,
函数 是定义在 上的偶函数,当 时, .
因此, ;
(2)由 ,得出 ,则问题等价于当直线 与函数 的图象有
个交点时,求实数 的取值范围.
作出函数 与函数 的图象如下图所示:
( )f x
( ) ( )g x f x= ( ) ( )h x g x m= − 6 m
( ) 2
2
2 1, 0
2 1, 0
x x xf x
x x x
+ − <= − − ≥
( )1,2
0x < ( )f x− ( )y f x= 0x <
( )y f x= R
( ) 0h x = ( )m g x= y m= ( )y g x= 6
m ( ) ( )g x f x=
m
0x < 0x− > ( ) ( ) ( )2 22 1 2 1f x x x x x= − − × − − = + −
( )y f x= R 0x < ( ) ( ) 2 2 1f x f x x x= − = + −
( ) 2
2
2 1, 0
2 1, 0
x x xf x
x x x
+ − <= − − ≥
( ) 0h x = ( )m g x= y m= ( )y g x= 6
m
y m= ( ) ( )g x f x=
由图象可知,当 时,直线 与函数 的图象有 个交点,
此时,函数 有 个零点.
因此,实数 的取值范围是 .
【点睛】本题考查偶函数解析式的求解,同时也考查了利用函数的零点个数求参数,一般利
用参变量分离法转化为两个函数图象的交点个数问题,利用数形结合思想求解,考查数形结
合思想的应用,属于中等题.
22.已知函数 ( 且 ).
(1)函数 是否过定点?若是求出该定点,若不是,说明理由.
(2)将函数 图象向下平移 个单位,再向左平移 个单位后得到函数 ,设函数
的反函数为 ,求 的解析式;
(3)在(2)的基础上,若函数 过点 ,且设函数 的定义域为 ,
若在其定义域内,不等式 恒成立,求 的取值范围.
【答案】(1)过定点 ;(2) ( 且 );(3) .
【解析】
【分析】
(1)在函数 的解析式中,令指数为零,可求出该函数所过定点的坐标;
(2)根据平移原则求出函数 的解析式,然后再根据同底数的对数函数与指数函数互
为反函数这一性质可得出函数 的解析式;
的
1 2m< < y m= ( )y g x= 6
( )y h x= 6
m ( )1,2
( ) 2 1xf x a −= + 0a > 1a ≠
( )f x
( )f x 1 2 ( )g x
( )g x ( )h x ( )h x
( )y h x= ( )4,2 ( )y h x= ( ]1,4
( ) ( ) ( )2 2 62 hh x x m h x ≤ + ⋅ + + m
( )2,2 ( ) logah x x= 0a > 1a ≠ [ )3,+∞
( )y f x=
( )y g x=
( )y h x=
(3)将点 代入函数 的解析式得出 ,令 ,由
,得出 ,利用函数单调性求出函数
在 上的最大值,即可得出实数 的取值范围.
【详解】(1) ( 且 ),令 ,得 ,
.
因此,函数 的图象恒过定点 ;
(2)将函数 的图象向下平移 个单位,得到函数 ( 且 )的图象,
再将所得函数的图象向左平移 个单位,可得到函数 ( 且 )的图象.
因此, ( 且 );
(3)由题意得 ,得 , 且 , ,则 ,
当 时, .
由 ,得 ,
即 ,
令 ,则不等式 对任意的 恒成立,
对任意的 恒成立,构造函数 ,其中 .
则函数 在区间 上单调递增,则该函数的最大值为 ,
,因此,实数 的取值范围是 .
【点睛】本题考查了指数图象恒过定点问题、反函数解析式的求解以及对数型函数不等式在
某区间上恒成立问题的求解,利用换元思想转化为二次不等式在区间上恒成立,并结合参变
量分离法求解是解题关键,考查化归与转化思想的应用,属于中等题.
23.已知 是定义在 上的奇函数.
(1)当 时, ,若当 时, 恒成立,求
的最小值;
( )4,2 ( )y h x= 2a = ( ]2log 0,2t x= ∈
( ) ( ) ( )2 2 62 hh x x m h x ≤ + ⋅ + +
2 2m t t
≥ − +
2 2y t t
= − + ( ]0,2t ∈ t
( ) 2 1xf x a −= + 0a > 1a ≠ 2 0x − = 2x =
( ) 02 1 2f a∴ = + =
( )y f x= ( )2,2
( )y f x= 1 2xy a −= 0a > 1a ≠
2 ( ) xg x a= 0a > 1a ≠
( ) logah x x= 0a > 1a ≠
( )4 log 4 2ah = = 2 4a = 0a > 1a ≠ 2a∴ = ( ) 2logh x x=
( ]1,4x∈ ( ) ( ]2log 0,2h x x= ∈
( ) ( ) ( )2 2 62 hh x x m h x ≤ + ⋅ + + ( )2 2
2 2 2log 2 log log 6x x m x+ ≤ + +
( )2
2 2 2log 2 2log log 6x x m x+ ≤ + +
( ]2log 0,2t x= ∈ ( )22 2 6t t mt+ ≤ + + ( ]0,2t ∈
2 2m t t
∴ ≥ − + ( ]0,2t ∈ 2 2y t t
= − + ( ]0,2t ∈
2 2y t t
= − + ( ]0,2 max
22 2 32y = − + =
3m∴ ≥ m [ )3,+∞
( )y f x= R
0x > ( ) 2 3 6f x x x= − + [ ]3 1x∈ − −, ( )n f x m≤ ≤
m n−
(2)若 的图像关于 对称,且 时, ,求当
时, 的解析式;
(3)当 时, .若对任意的 ,不等式 恒成立,
求实数 的取值范围.
【答案】(1) 的最小值为 ;(2) ;(3) .
【解析】
试题分析:(1) 取最小值时,m,n 为函数在 上最大值与最小值,先求函数在
上最值,再根据奇函数性质得在 上最大值与最小值,(2)先根据函数两个对称
性(一个关于原点对称,一个关于 对称)推导出函数周期,根据周期性只需求出
解析式,根据关于 对称,只需求出 上解析式,根据奇函数性质根据 解析
式可得 上解析式,(3)先根据函数解析式得到 ,转化不等式为
,再根据函数单调性得 ,最后根据不等式恒成立,利用变量
分离法求实数 的取值范围.
试题解析:(1) ,当 时,
.
,因为函数 是奇函数,所以当 时,
, .
所以 , , 的最小值为 .
(2)由 为奇函数,得 ;又 的图像关于 对称,得
;∴ 即 ∴
当 , ;
当 , ;
( )f x 3x = ( )3 0x∈ − , ( ) 3 1xf x x= − +
( )9 6x∈ − −, ( )f x
0x ≥ ( ) 2f x x= [ ]2x t t,∈ + ( ) ( )2f x t f x+ ≥
t
m n− 9
4
( ) 63 5xf x x+= − + + 2t ≥
m n− [ ]3 1,− −
[ ]1 3, [ ]3 1,− −
3x = ( )3 6,
3x = ( )0 3, ( )3 0,−
( )0 3, ( ) ( )2 2f x f x=
( ) ( )2f x t f x+ ≥ 2x t x+ ≥
t
( ) 2
2 3 153 6 2 4f x x x x = − + = − +
[ ]1 3x∈ ,
( )min
3 15
2 4f x f = =
( ) ( )max 3 6f x f= = ( )f x [ ]3 1x∈ − −,
( )max
15
4f x = − ( )min 6f x = −
( )min 6n f x≤ = − ( )max
15
4m f x≥ = − m n− 9
4
( )f x ( ) ( ) 0f x f x− + = ( )f x 3x =
( ) ( )6f x f x= − ( ) ( )6 0f x f x− + − = ( ) ( )6f t f t+ = − ( ) ( )12f t f t+ =
( )0 3x∈ , ( ) ( ) 3 1xf x f x x−= − − = − − −
( )3 6x∈ , ( ) ( ) 66 3 7xf x f x x−= − = − + −
又 ,当 时,
(3)易知 , ;
, ;综上,对任 ,
∴ 对任意的 恒成立,又 在 上递增,
∴ ,即 对任意的 恒成立.
∴ ∴
12T = ( )9 6x∈ − −, ( ) ( ) 612 3 5xf x f x x+= + = − + +
0x ≥ ( ) ( ) ( )2 22 2 2 2f x x x f x= = =
0x ≤ ( ) ( ) ( )2 22 2 2 2f x x x f x= − = − = x R∈ ( ) ( )2 2f x f x=
( ) ( )2f x t f x+ ≥ [ ]2x t t∈ +, ( )f x R
2x t x+ ≥ ( )2 1t x≥ − [ ]2x t t∈ +,
( )( )2 1 2t t≥ − + 2t ≥