高考数学复习专题练习第4讲 函数y＝Asin(ωx＋φ)的图像

高考数学复习专题练习第4讲 函数y＝Asin(ωx＋φ)的图像

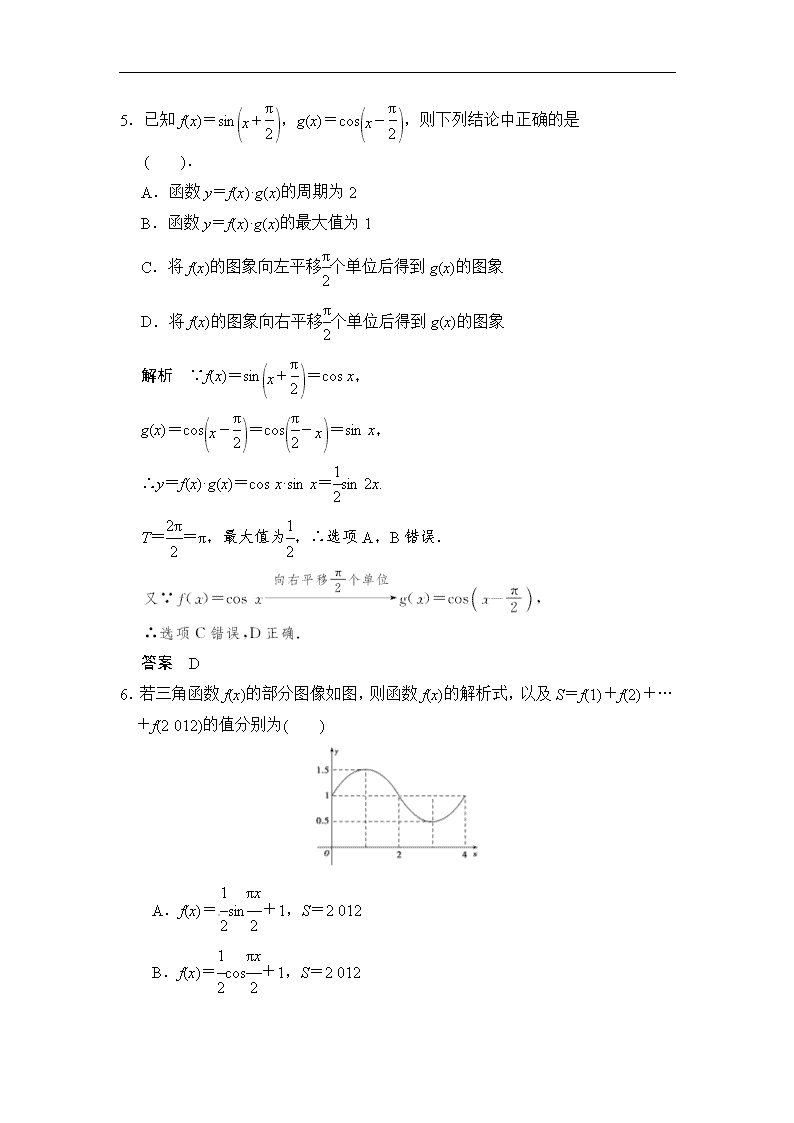
第4讲 函数y＝Asin(ωx＋φ)的图像 一、选择题 ‎1．将函数y＝cos 2x的图像向右平移个单位，得到函数y＝f(x)·sin x的图像，则f(x)的表达式可以是(　　)‎ A．f(x)＝－2cos x　　　 B．f(x)＝2cos x[来 C．f(x)＝sin 2x D．f(x)＝(sin 2x＋cos 2x)‎ 解析 平移后对应的函数解析式是y＝cos 2＝sin 2x＝2sin xcos x，故函数f(x)的表达式可以是f(x)＝2cos x.‎ 答案 B ‎2．将函数y＝sin 2x的图象向左平移φ(φ>0)个单位，所得图象对应的函数为偶函数，则φ的最小值为(　　)．‎ A. B. C. D. 解析　将函数y＝sin 2x的图象向左平移φ个单位，得到函数y＝sin 2(x＋φ)＝sin(2x＋2φ)的图象，由题意得2φ＝＋kπ(k∈Z)，故φ的最小值为.‎ 答案　C ‎3． 已知f(x)＝－2sin(ωx＋φ)的部分图像如图所示，则f(x)的表达式为(　　)‎ A．f(x)＝－2sin B．f(x)＝－2sin C．f(x)＝－2sin D．f(x)＝－2sin 解析 由条件可知：－＝π＝T，[来源:Zxxk.Com]‎ ‎∴T＝π，由＝得ω＝.‎ 在五点作图中，x＝π为第四点，‎ ‎∴×＋φ＝π，解得φ＝，‎ ‎∴f(x)＝－2sin.‎ 答案 A ‎4．把函数y＝cos 2x＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是 (　　)．‎ 解析　把函数y＝cos 2x＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y＝cos x＋1的图象，然后把所得函数图象向左平移1个单位长度，再向下平移1个单位长度，得到函数y＝cos(x＋1)的图象，故选A.‎ 答案　A ‎5．已知f(x)＝sin，g(x)＝cos，则下列结论中正确的是 (　　)．‎ A．函数y＝f(x)·g(x)的周期为2‎ B．函数y＝f(x)·g(x)的最大值为1‎ C．将f(x)的图象向左平移个单位后得到g(x)的图象 D．将f(x)的图象向右平移个单位后得到g(x)的图象 解析　∵f(x)＝sin＝cos x，‎ g(x)＝cos＝cos＝sin x，‎ ‎∴y＝f(x)·g(x)＝cos x·sin x＝sin 2x.‎ T＝＝π，最大值为，∴选项A，B错误．‎ 答案　D ‎6．若三角函数f(x)的部分图像如图，则函数f(x)的解析式，以及S＝f(1)＋f(2)＋…＋f(2 012)的值分别为(　　)‎ A．f(x)＝sin＋1，S＝2 012‎ B．f(x)＝cos＋1，S＝2 012‎ C．f(x)＝sin＋1，S＝2 012.5‎ D．f(x)＝cos＋1，S＝2 012.5‎ 解析 根据已知图像，可设f(x)＝Asin(ωx＋φ)＋1(ω>0，A>0)，由T＝4得＝4，‎ ‎∴ω＝，A＝＝＝，又f(0)＝sin φ＋1＝1，∴sin φ＝0，得 φ＝0，∴f(x)＝sin ＋1.‎ 又f(1)＋f(2)＋f(3)＋f(4)＝1.5＋1＋0.5＋1＝4，∴S＝f(1)＋f(2)＋…＋f(2 012)＝503×[f(1)＋f(2)＋f(3)＋f(4)]＝503×4＝2 012，故选A.‎ 答案 A 二、填空题 ‎7. 已知函数f(x)＝sin(ωx＋φ)ω>0，0<φ<的部分图象如图所示，则ω＝________，φ＝________.‎ 解析　因为＝－＝，所以T＝π，ω＝＝2.将代入解析式可得：π＋φ＝2kπ＋(k∈Z)，即φ＝2kπ＋(k∈Z)，又0<φ<，所以φ＝.‎ 答案　2　 ‎8．已知函数f(x)＝3sin(ω＞0)和g(x)＝2cos(2x＋φ)＋1的图象的对称轴完全相同，若x∈，则f(x)的取值范围是________．‎ 解析　∵f(x)与g(x)的图象的对称轴完全相同，∴f(x)与g(x)的最小正周期相等，∵ω＞0，∴ω＝2，∴f(x)＝3sin，∵0≤x≤，∴－≤2x－≤，∴－≤sin≤1，∴－≤3sin≤3，即f(x)的取值范围是.‎ 答案　 ‎9．已知函数f(x)＝－2sin(2x＋φ)(|φ|<π)，若是f(x)的一个单调递增区间，则φ的值为________．‎ 解析　令＋2kπ≤2x＋φ≤＋2kπ，k∈Z，k＝0时，有－≤x≤－，此时函数单调递增，若是f(x)的一个单调递增区间，则必有 解得故φ＝.‎ 答案　 ‎10．设函数y＝sin(ωx＋φ)的最小正周期为π，且其图象关于直线x＝对称，则在下面四个结论中：‎ ‎①图象关于点对称；②图象关于点对称；③在上是增函数；④在上是增函数．‎ 其中正确结论的编号为________．‎ 解析　∵y＝sin(ωx＋φ)的最小正周期为π，‎ ‎∴ω＝＝2，又其图象关于直线x＝对称，‎ ‎∴2×＋φ＝kπ＋(k∈Z)，∴φ＝kπ＋，k∈Z.‎ 由φ∈，得φ＝，∴y＝sin.‎ 令2x＋＝kπ(k∈Z)，得x＝－(k∈Z)．‎ ‎∴y＝sin关于点对称．故②正确．‎ 令2kπ－≤2x＋≤2kπ＋(k∈Z)，得 kπ－≤x≤kπ＋(k∈Z)．‎ ‎∴函数y＝sin的单调递增区间为 (k∈Z)．‎ ‎∵(k∈Z)．∴④正确．‎ 答案　②④‎ 三、解答题 ‎11．已知函数f(x)＝Asin(ωx＋φ)的部分图像如图所 示．‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)求函数g(x)＝f－f的单调递增区间．‎ 解 (1)由题设图像知，周期T＝2＝π，‎ 所以ω＝＝2，‎ 因为点在函数图像上，‎ 所以Asin＝0，‎ 即sin＝0.‎ 又因为0<φ<，‎ 所以<＋φ<，‎ 从而＋φ＝π，即φ＝.‎ 又点(0,1)在函数图像上，‎ 所以Asin＝1，得A＝2.‎ 故函数f(x)的解析式为 f(x)＝2sin.‎ ‎(2)g(x)＝2sin－2sin ‎＝2sin 2x－2sin ‎＝2sin 2x－2 ‎＝sin 2x－cos 2x ‎＝2sin，‎ 由2kπ－≤2x－≤2kπ＋， ‎ 得kπ－≤x≤kπ＋，k∈Z.‎ 所以函数g(x)的单调递增区间是，k∈Z.‎ ‎12．已知向量m＝(sin x,1)，n＝(Acos x，cos 2x)(A＞0)，函数f(x)＝m·n的最大值为6.‎ ‎(1)求A；‎ ‎(2)将函数y＝f(x)的图象向左平移个单位，再将所得图象上各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)在上的值域．‎ 解　(1)f(x)＝m·n＝Asin xcos x＋cos 2x ‎＝A＝A sin.‎ 因为A＞0，由题意知A＝6.‎ ‎(2)由(1)知f(x)＝6sin.‎ 将函数y＝f(x)的图象向左平移个单位后得到 y＝6sin＝6sin的图象；‎ 再将得到图象上各点横坐标缩短为原来的倍，纵坐标不变，得到y＝6sin的图象．‎ 因此g(x)＝6sin.‎ 因为x∈，所以4x＋∈，‎ 故g(x)在上的值域为[－3,6]．‎ ‎13．已知函数f(x)＝2sin＋cos－sin(x＋π)．‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)若将f(x)的图象向右平移个单位，得到函数g(x)的图象，求函数g(x)在区间[0，π]上的最大值和最小值．‎ 解　(1)因为f(x)＝sin＋sin x ‎＝cos x＋sin x＝2 ‎＝2sin，‎ 所以f(x)的最小正周期为2π.‎ ‎(2)∵将f(x)的图象向右平移个单位，得到函数g(x)的图象，‎ ‎∴g(x)＝f＝2sin[＋]‎ ‎＝2sin.‎ ‎∵x∈[0，π]，∴x＋∈，‎ ‎∴当x＋＝，即x＝时，sin＝1，g(x)取得最大值2.‎ 当x＋＝，即x＝π时，sin＝－，g(x)取得最小值－1.‎ ‎14．设函数f(x)＝cos＋sin2x.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)设函数g(x)对任意x∈R，有g＝g(x)，且当x∈时，g(x)＝－f(x)．求g(x)在区间[－π，0]上的解析式．‎ 解　(1)f(x)＝cos＋sin2x ‎＝＋ ‎＝－sin 2x，‎ 故f(x)的最小正周期为π.‎ ‎(2)当x∈时，g(x)＝－f(x)＝sin 2x，故 ‎①当x∈时，x＋∈.‎ 由于对任意x∈R，g＝g(x)，‎ 从而g(x)＝g＝sin ‎＝sin(π＋2x)＝－sin 2x.‎ ‎②当x∈时，x＋π∈.‎ 从而g(x)＝g(x＋π)＝sin[2(x＋π)]＝sin 2x.‎ 综合①、②得g(x)在[－π，0]上的解析式为 g(x)＝