中学生标准学术能力诊断性测试2020年1月试题 数学(理)
中学生标准学术能力诊断性测试2020年1月测试
理科数学试卷(一卷)
本试卷共150分,考试时间120分钟。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合A={x|-1
logba的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
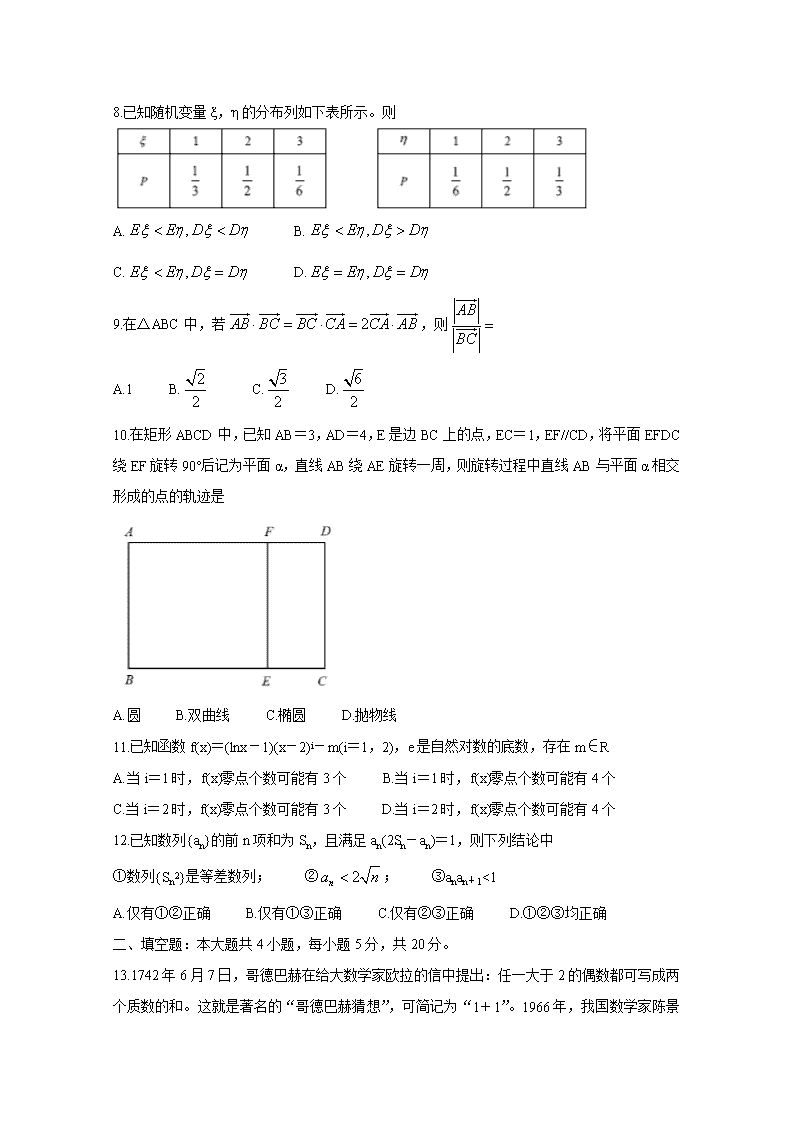
8.已知随机变量ξ,η的分布列如下表所示。则
A. B.
C. D.
9.在△ABC中,若,则
A.1 B. C. D.
10.在矩形ABCD中,已知AB=3,AD=4,E是边BC上的点,EC=1,EF//CD,将平面EFDC绕EF旋转90°后记为平面α,直线AB绕AE旋转一周,则旋转过程中直线AB与平面α相交形成的点的轨迹是
A.圆 B.双曲线 C.椭圆 D.抛物线
11.已知函数f(x)=(lnx-1)(x-2)i-m(i=1,2),e是自然对数的底数,存在m∈R
A.当i=1时,f(x)零点个数可能有3个 B.当i=1时,f(x)零点个数可能有4个
C.当i=2时,f(x)零点个数可能有3个 D.当i=2时,f(x)零点个数可能有4个
12.已知数列{an}的前n项和为Sn,且满足an(2Sn-an)=1,则下列结论中
①数列{Sn2}是等差数列; ②; ③anan+1<1
A.仅有①②正确 B.仅有①③正确 C.仅有②③正确 D.①②③均正确
二、填空题:本大题共4小题,每小题5分,共20分。
13.1742年6月7日,哥德巴赫在给大数学家欧拉的信中提出:任一大于2的偶数都可写成两个质数的和。这就是著名的“哥德巴赫猜想”,可简记为“1+1”。1966年,
我国数学家陈景润证明了“1+2”,获得了该研究的世界最优成果,若在不超过30的所有质数中,随机选取两个不同的数,则两数之和不超过30的概率是 。
14.已知△ABC的面积等于1,若BC=1,则当这个三角形的三条高的乘积取最大值时,sinA= 。
15.已知F是椭圆C:的一个焦点,P是C上的任意一点,则|FP|称为椭圆C的焦半径。设C的左顶点与上顶点分别为A、B,若存在以A为圆心,|FP|为半径长的圆经过点B,则椭圆C的离心率的最小值为 。
16.设函数f(x)=|x3-6x2+ax+b|,若对任意的实数a和b,总存在x0∈[0,3],使得f(x0)≥m,则实数m的最大值为 。
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:60分。
17.(12分)已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边经过点P(-1,)。
(1)求的值;
(2)求函数f(x)=sin2(x+α)-cos2(x-α)(x∈R)的最小正周期与单调递增区间。
18.(12分)如图,多面体ABCDEF中,四边形ABEF和四边形CDFE是两个全等的菱形,AB=2,∠BAF=∠ECD=60°。
(1)求证:BD⊥DC;
(2)如果二面角B-EF-D的平面角为60°,求直线BD与平面BCE所成角的正弦值。
19.(12分)已知等比数列{an}的公比q>1,且a1+a3+a5=42,a3+9是a1,a5的等差中项。数列{bn}的通项公式。
(1)求数列{an}的通项公式;
(2)证明:。
20.(12分)已知抛物线C:x2=2py(p>0),焦点为F,准线与y轴交于点E。若点P在C上,横坐标为2,且满足:。
(1)求抛物线C的方程;
(2)若直线PE交x轴于点Q,过点Q做直线l,与抛物线C有两个交点M,N(其中,点M在第一象限)。若,当λ∈(1,2)时,求的取值范围。
21.(12分)已知函数f(x)=(x+1)(ex-1)。
(1)求f(x)在点(-1,f(-1))处的切线方程;
(2)若方程f(x)=b有两个实数根x1,x2,且x10。若曲线C上所有点均在直线l的右上方,求a的取值范围。
23.[选修4—5:不等式选讲](10分)
已知正数x,y,z满足x+y+z=1。
(1)求证:;(2)求的最小值。