2021届课标版高考文科数学大一轮复习精练：§2-6 函数的图象（试题部分）

2021届课标版高考文科数学大一轮复习精练：§2-6 函数的图象（试题部分）

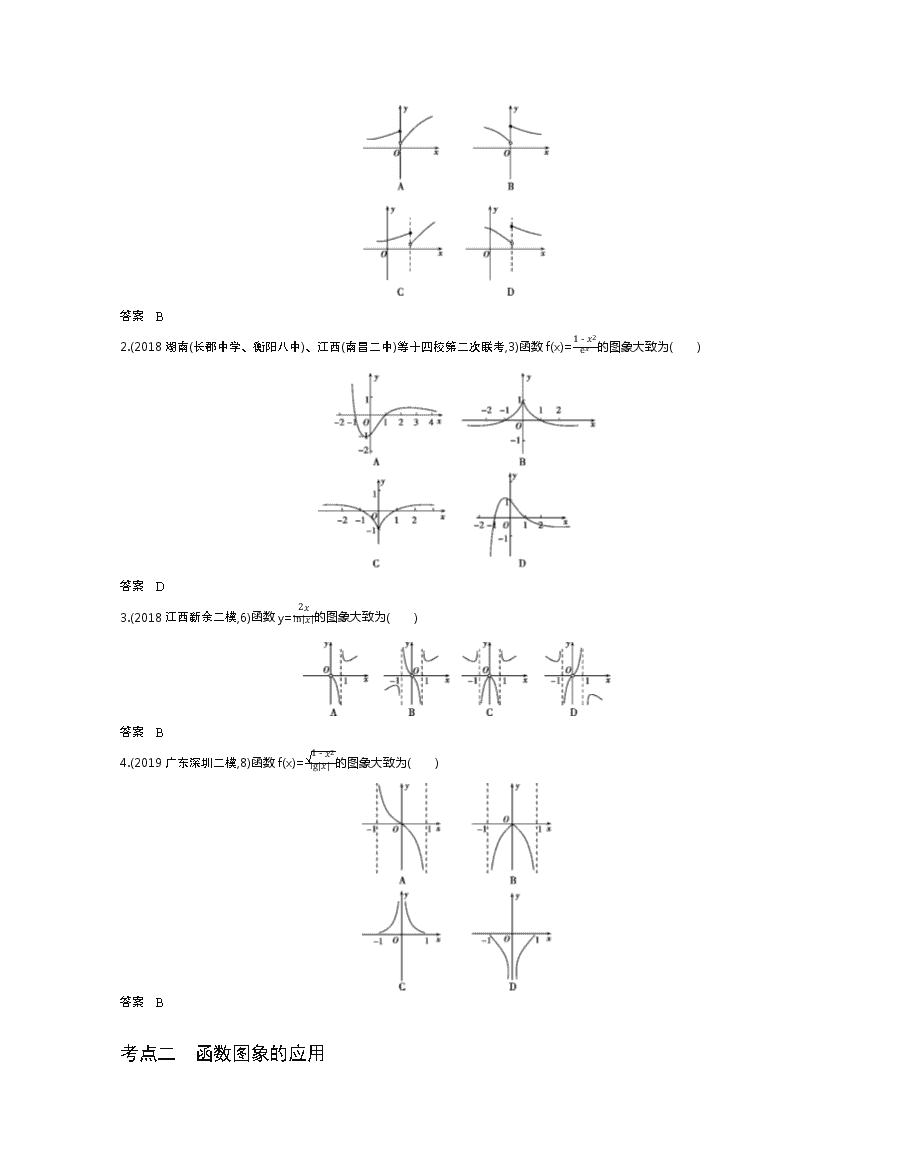
‎§2.6　函数的图象 探考情 悟真题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 函数的 图象 在掌握基本初等函数图象的基础上,利用函数变化的快慢、函数的定义域、奇偶性、单调性、函数图象过定点等特点对函数图象作出判断 ‎2018课标全国Ⅱ,3,5分 函数图象的判断 函数奇偶性的应用 ‎★★☆‎ ‎2018课标全国Ⅲ,9,5分 函数图象的判断 用求导法判断函数的单调性 ‎2017课标全国Ⅰ,8,5分 函数图象的判断 函数奇偶性的应用 ‎2016课标全国Ⅰ,9,5分 函数图象的判断 函数零点 ‎2019课标全国Ⅰ,5,5分 函数图象的判断 函数性质的应用 函数图象 的应用 掌握函数图象的平移变换、对称变换、伸缩变换和翻折变换,熟悉各种变换的过程和特点,并由此解决相关问题;利用函数图象研究函数的性质,根据性质解决相关问题以及利用函数图象解决最值问题、判断方程解的个数 ‎2015课标Ⅰ,12,5分 函数图象的变换 ‎—‎ ‎★★☆‎ ‎2016课标全国Ⅱ,12,5分 函数图象的应用 ‎—‎ 分析解读 ‎1.高考主要考查由函数解析式画出函数的图象,两个函数图象的交点情况.近几年考查了用图象表示函数.‎ ‎2.在数学中,由“形”到“数”比较明显,由“数”到“形”需要意识,而试题中主要是由“数”到“形”.在解答题中,要注意推理论证的严密性,避免出现以图代证的现象,利用图象研究函数的性质,特别是在判断非常规方程根的个数时,此法有时“妙不可言”,这是数形结合思想在“数”中的重要体现.‎ 破考点 练考向 ‎【考点集训】‎ 考点一　函数的图象 ‎1.(2018湖南长沙第一中学高考模拟,6)已知函数f(x)=ex‎,x≤e,‎lnx,x>e,‎则函数y=f(e-x)的大致图象是(　　)‎ 答案　B　‎ ‎2.(2018湖南(长郡中学、衡阳八中)、江西(南昌二中)等十四校第二次联考,3)函数f(x)=‎1-‎x‎2‎ex的图象大致为(　　)‎ 答案　D　‎ ‎3.(2018江西新余二模,6)函数y=‎2xln|x|‎的图象大致为(　　)‎ 答案　B　‎ ‎4.(2019广东深圳二模,8)函数f(x)=‎1-‎x‎2‎lg|x|‎的图象大致为(　　)‎ 答案　B　‎ 考点二　函数图象的应用 ‎　(2019安徽马鞍山二模,7)已知定义在R上的函数f(x),g(x)满足g(x)=f(|x-1|),则函数y=g(x)的图象关于(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.直线x=-1对称 B.直线x=1对称 C.原点对称 D.y轴对称 答案　B　‎ 炼技法 提能力 ‎【方法集训】‎ 方法1　函数图象的识辨方法 ‎1.(2018安徽淮北一模,8)函数f(x)=‎1‎x+ln|x|的图象大致为(　　)‎ 答案　B　‎ ‎2.(2019山西吕梁4月模拟,3)函数f(x)=|x|sin x的图象大致是(　　)‎ 答案　A　‎ ‎3.(2018福建三明第一中学开学考试,9)给出下列四个函数:‎ ‎①y=x·sin x;②y=x·cos x;③y=x·|cos x|;④y=x·2x.‎ 这四个函数的部分图象如图,但顺序被打乱,则按照从左到右的顺序将图象对应的函数序号排列正确的一组是(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.①④②③ B.①④③② C.④①②③ D.③④②①‎ 答案　A　‎ 方法2　函数图象的应用 ‎1.(2018湘东五校联考,11)已知函数f(x)=‎|x+1|,-7≤x≤0,‎lnx,e‎-2‎≤x≤e,‎g(x)=x2-2x,设a为实数,若存在实数m,使得f(m)-2g(a)=0,则实数a的取值范围为(　　)‎ A.[-1,+∞) B.(-∞,-1]∪[3,+∞) C.[-1,3] D.(-∞,3]‎ 答案　C　‎ ‎2.(2018河南焦作第四次模拟,12)已知函数f(x)=ex-1-e1-x+4,若方程f(x)=kx+4-k(k>0)有三个不同的根x1,x2,x3,则x1+x2+x3=(　　)‎ A.0 B.2 C.6 D.3‎ 答案　D　‎ ‎3.(2020届黑龙江哈尔滨第六中学调研,7)若x1是方程xex=4的解,x2是方程xln x=4的解,则x1·x2等于(　　)‎ A.4 B.2 C.e D.1‎ 答案　A　‎ ‎【五年高考】‎ A组　统一命题·课标卷题组 考点一　函数的图象 ‎1.(2018课标全国Ⅲ,9,5分)函数y=-x4+x2+2的图象大致为(　　)‎ 答案　D　‎ ‎2.(2017课标全国Ⅲ,7,5分)函数y=1+x+sinxx‎2‎的部分图象大致为(　　)‎ 答案　D　‎ ‎3.(2017课标全国Ⅰ,8,5分)函数y=sin2x‎1-cosx的部分图象大致为(　　)‎ 答案　C　‎ ‎4.(2016课标全国Ⅰ,9,5分)函数y=2x2-e|x|在[-2,2]的图象大致为(　　)‎ 答案　D　‎ ‎5.(2015课标Ⅱ,11,5分)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为(　　)‎ 答案　B　‎ 考点二　函数图象的应用 ‎1.(2016课标全国Ⅱ,12,5分)已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3|与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则‎∑‎i=1‎mxi=(　　)　　　　　 　　　　　　 　　　　　　 ‎ A.0 B.m C.2m D.4m 答案　B　‎ ‎2.(2015课标Ⅰ,12,5分)设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且f(-2)+f(-4)=1,则a=(　　)‎ A.-1 B.1 C.2 D.4‎ 答案　C　‎ B组　自主命题·省(区、市)卷题组 ‎1.(2019浙江,6,4分)在同一直角坐标系中,函数y=‎1‎ax,y=logax+‎‎1‎‎2‎(a>0,且a≠1)的图象可能是(　　)‎ 答案　D　‎ ‎2.(2018浙江,5,4分)函数y=2|x|sin 2x的图象可能是(　　)‎ 答案　D　‎ ‎3.(2016浙江,3,5分)函数y=sin x2的图象是(　　)‎ 答案　D　‎ C组　教师专用题组 考点一　函数的图象 ‎1.(2014江西,10,5分)在同一直角坐标系中,函数y=ax2-x+a‎2‎与y=a2x3-2ax2+x+a(a∈R)的图象不可能‎···‎的是(　　)‎ 答案　B　‎ ‎2.(2013课标Ⅰ,9,5分)函数f(x)=(1-cos x)sin x在[-π,π]上的图象大致为(　　)‎ 答案　C　‎ ‎3.(2013福建,5,5分)函数f(x)=ln(x2+1)的图象大致是(　　)‎ 答案　A　‎ ‎4.(2013山东,9,5分)函数y=xcos x+sin x的图象大致为(　　)‎ 答案　D　‎ 考点二　函数图象的应用 ‎1.(2014辽宁,10,5分)已知f(x)为偶函数,当x≥0时, f(x)=cos πx,x∈‎0,‎‎1‎‎2‎,‎‎2x-1,x∈‎1‎‎2‎‎,+∞‎,‎则不等式f(x-1)≤‎1‎‎2‎的解集为(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.‎1‎‎4‎‎,‎‎2‎‎3‎∪‎4‎‎3‎‎,‎‎7‎‎4‎ B.‎-‎3‎‎4‎,-‎‎1‎‎3‎∪‎‎1‎‎4‎‎,‎‎2‎‎3‎ C.‎1‎‎3‎‎,‎‎3‎‎4‎∪‎4‎‎3‎‎,‎‎7‎‎4‎ D.‎-‎3‎‎4‎,-‎‎1‎‎3‎∪‎‎1‎‎3‎‎,‎‎3‎‎4‎ 答案　A　‎ ‎2.(2014湖北,15,5分)如图所示,函数y=f(x)的图象由两条射线和三条线段组成.‎ 若∀x∈R, f(x)>f(x-1),则正实数a的取值范围为　　　　. ‎ 答案　‎‎0,‎‎1‎‎6‎ ‎【三年模拟】‎ 时间:35分钟　分值:45分 一、选择题(每小题5分,共35分)‎ ‎1.(2019安徽1号卷A10联盟4月联考,6)已知函数f(x)=‎10(x‎2‎+1)‎x·‎e‎|x|‎,则函数f(x)的图象大致为(　　)‎ 答案　A　‎ ‎2.(2019湖南娄底二模,8)函数f(x)=‎(ex-e‎-x)cosxx‎2‎的部分图象大致是(　　)‎ 答案　A　‎ ‎3.(2020届广东广宁中学模拟,5)函数y=f(x)在区间‎-π‎2‎,‎π‎2‎上的大致图象如图,则f(x)的解析式可能是(　　)‎ ‎　　　　　　 　　　　　　 　　　　　　 ‎ A.f(x)=ln|sin x| B.f(x)=ln(cos x)‎ C.f(x)=-sin|tan x| D.f(x)=-tan(cos x)‎ 答案　B　‎ ‎4.(2020届河南濮阳模拟,10)函数f(x)=(x-1)ln|x|的图象可能为(　　)‎ 答案　A　‎ ‎5.(2018湖南衡阳二模,9)已知函数f(x)=dax‎2‎+bx+c(a,b,c,d∈R)的图象如图所示,则(　　)‎ A.a>0,b>0,c<0,d>0 B.a<0,b>0,c<0,d>0‎ C.a<0,b>0,c>0,d>0 D.a>0,b<0,c>0,d>0‎ 答案　B　‎ ‎6.(2018安徽江淮十校第三次(4月)联考,10)若直角坐标系内A、B两点满足:(1)点A、B都在f(x)图象上;(2)点A、B关于原点对称,则称点对(A,B)是函数f(x)的一个“和谐点对”,(A,B)与(B,A)可看作一个“和谐点对”.已知函数f(x)=x‎2‎‎+2x(x<0),‎‎2‎ex‎(x≥0),‎则f(x)的“和谐点对”有(　　)‎ A.1个 B.2个 C.3个 D.4个 答案　B　‎ ‎7.(2019河南天一大联考阶段性测试(五),12)已知函数f(x)=ex‎,x<0,‎‎-x‎2‎+‎5‎‎2‎x,x≥0,‎若方程f(x)=kx+1有3个不同的实根,则实数k的取值范围为(　　)‎ A.(-∞,0] B.‎0,‎‎1‎‎2‎ C.‎1‎‎2‎‎,+∞‎ D.(0,+∞)‎ 答案　B　‎ 二、填空题(每小题5分,共10分)‎ ‎8.(2020届河南濮阳模拟,16)已知函数f(x)=log‎2‎x(x>0),‎‎3‎x‎(x≤0),‎且关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是　　　　. ‎ 答案　(1,+∞)‎ ‎9.(2019福建龙岩教学质量检查,15)设函数y=f(x)的图象与y=‎1‎‎3‎x+a的图象关于直线y=-x对称,且f(-3)+f‎-‎‎1‎‎3‎=4,则实数a=　　　　. ‎ 答案　2‎