高中数学：一《平行线等分线段定理》教案4（新人教A版选修4-1）

高中数学：一《平行线等分线段定理》教案4（新人教A版选修4-1）

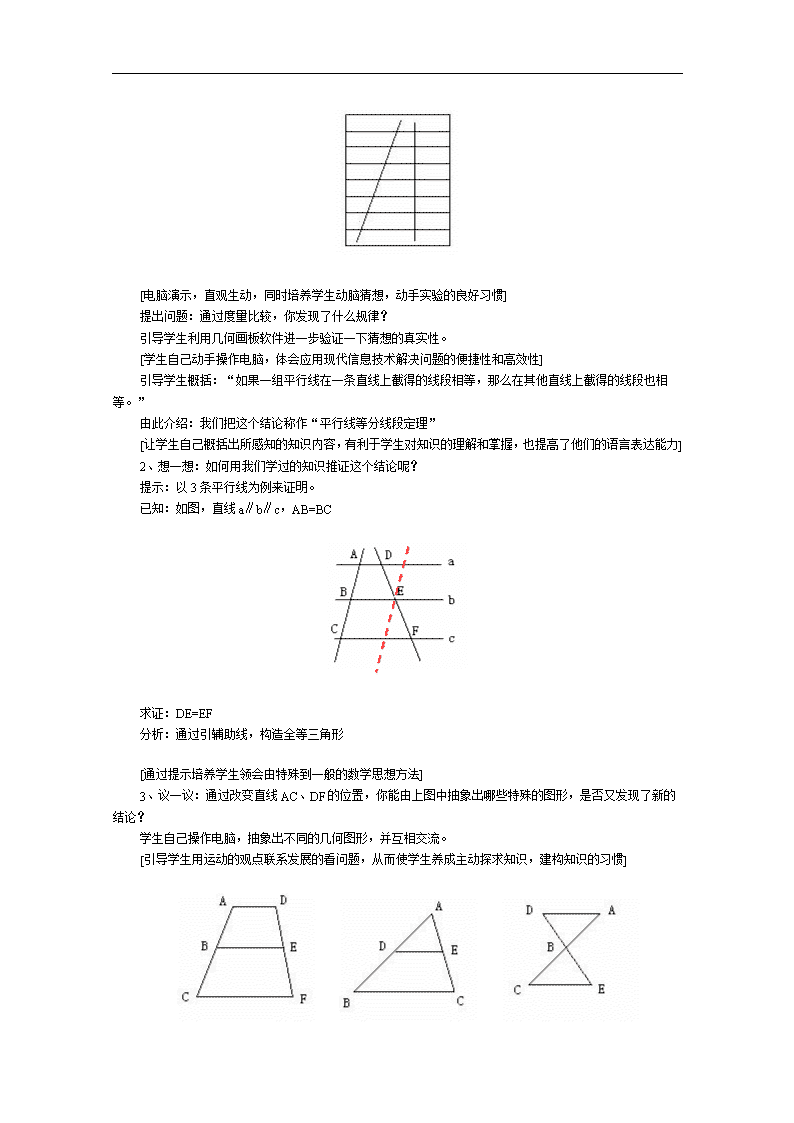
平行线等分线段定理 ‎ ‎        【教材分析】                教学重点：根据新的课程标准，将平行线等分线段定理及其推论的应用作为重点，同时将自主探索、动手操作、协作交流意识的培养作为重点。         教学难点：定理的灵活应用是本节的难点。在教学过程中循序渐进的设计“猜一猜”、“想一想”、“议一议”、“做一做”、“试一试”以突破这一难点。         【设计理念】         现代教学论指出，教学过程是师生交往、积极互动、共同发展的过程。没有交往，没有互动，就不存在或未发生教学，那些只有教学的形式表现而无实质性交往发生的“教学”，是假教学。把教学本质定位为交往，是对教学过程的正本清源。对教学而言，交往意味着对话，意味着参与，意味着相互建构，它不仅是一种教学活动方式，更是弥漫、充盈于师生之间的一种教育情境和精神氛围。对学生而言，交往意味着心态的开放，主体性的凸现，个性的张显，创造性的解放。对教师而言，交往意味着上课不是传授知识，而是一起分享理解；上课不是无谓的牺牲和时光的耗费，而是生命活动、专业成长和自我实现的过程。交往还意味着教师角色定位的转换:教师由教学中的主角转向“平等中的首席”，从传统的知识传授者转向现代的学生发展的促进者。         根据新的课程标准，结合本班学生实际，改变传统的严格意义上的教师教和学生学，力求师生互教互学， 彼此形成一个真正的“学习共同体”。让学生成为学习活动的主人，教师成为学生学习的组织者和合作者，而不是权威的讲授者。教师可以根据学生的提问或者活动中可能出现的某些情况，提供示范、建议和指导，引导学生们大胆阐述并讨论他们的观点，让学生说明他们所获得的结论的有效性，并对结论进行评价。学生学习的过程不是学生被动地吸收课本上的现成结论，而是一个学生亲自参与丰富、生动的思维活动，经历实践和创新的过程。         【教学目标】 知识目标：能用语言及结合图形的符号语言叙述平行线等分线段定理和它的两个推论；用它们能初步解决证明线段相等和计算线段长度的问题；会用尺规作图法等分一条已知线段；能独自处理等分实际物体的问题。         技能目标：通过观察和动手操作，经历和体验定理的产生过程，培养实验操作能力。         身心素质目标：主动探索，敢于实验，勇于发现，合作交流。         【教学流程】         一、创设问题情境，激发学生探索的欲望，导入课题。         1、提出问题：学校准备为教室的窗户安装防护栏，在没有尺的情况下如何将‎4米长钢筋截成等距离的5段？         2、指出：在实际生活中有很多问题用数学知识来解决既方便又适用。引发问题：如何解决呢？         3、引入课题——平行线等分线段定理         二、学生自主探求、协作交流、归纳概括、意义建构。         1、猜一猜：准备一张横格纸（其上横线是平行且等距的），任意画一条直线（如图），它被横线分成的各条线段的大小有什么关系？再多画几条看一看。‎ ‎        [电脑演示，直观生动，同时培养学生动脑猜想，动手实验的良好习惯]         提出问题：通过度量比较，你发现了什么规律？         引导学生利用几何画板软件进一步验证一下猜想的真实性。         [学生自己动手操作电脑，体会应用现代信息技术解决问题的便捷性和高效性]         引导学生概括：“如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等。”         由此介绍：我们把这个结论称作“平行线等分线段定理”         [让学生自己概括出所感知的知识内容，有利于学生对知识的理解和掌握，也提高了他们的语言表达能力]         2、想一想：如何用我们学过的知识推证这个结论呢？         提示：以3条平行线为例来证明。         已知：如图，直线a∥b∥c，AB=BC ‎        求证：DE=EF         分析：通过引辅助线，构造全等三角形 ‎        [通过提示培养学生领会由特殊到一般的数学思想方法]         3、议一议：通过改变直线AC、DF的位置，你能由上图中抽象出哪些特殊的图形，是否又发现了新的结论？         学生自己操作电脑，抽象出不同的几何图形，并互相交流。         [引导学生用运动的观点联系发展的看问题，从而使学生养成主动探求知识，建构知识的习惯]‎ ‎                                ‎ ‎                                 （1）                              （2）                                （3）‎ ‎        引导学生概括：“经过梯形一腰中点与底平行的直线，必平分另一腰。”如图（1）“经过三角形一边的中点与另一边平行的直线，必平分第三边。”如图（2）         指出：象图（3）这样的典型图例（8字形）在日后的证题中经常遇到。         [学生自己探求并总结出的结论，便于日后灵活应用。避免了死记结论的不良学习习惯。]         4、课堂练习：         ①如图：A、B、C、D把OE五等分，AA′∥BB′∥CC′∥DD′∥EE′，如果C′E′=‎8cm，那么OE′=      。‎ ‎        ②③④⑤⑥⑦⑧略         以上各题设计在authorware课件中，由学生自己操作电脑自我测评，做不对或不做都无法继续进行。         [遵循巩固性原则，同时避免了学生思维的懒惰性，克服了教师辅导的局限性，增强了课堂教学的实效性。]         5、试一试：应用平行线等分线段定理，你能用尺规作图法将一条已知线段五等分吗？         [培养学生动手操作能力和灵活运用新知识的能力。]         6、考一考：         ①在没有工具的情况下，你能想办法将‎10cm长的细绳7等分吗？         ②回答课前提出的问题：没有尺的情况下，要将‎4米长的钢筋5等分，你现在能想出几种办法？         [遵循巩固和发展相结合的原则，培养学生的创新意识和创造能力，并注重学生间的相互评价，提高学生用所学知识解决实际问题的能力]         三、交流经验、取长补短、共同进步。         1、学生整理信息；（整理随堂笔记，网上下载资料，访问同学共享信息）         2、学生汇报本节课的收获；          3、学生间交流彼此的教训；         4、教师提出建议和补充。         [学生汇报和交流使知识更加系统深入，教师的补充便于查缺补漏。]         四、课外活动         用一张矩形纸，你能折出一个等边三角形吗？‎ ‎                                                        ‎ ‎         如上图，先把矩形ABCD纸对折，设折痕为MN；再把B点叠在折痕线上，得到Rt△ABE，沿着EB线折叠，就能得到等边△EAF。想一想，这是为什么。         [带有一定挑战性的课后思考题能唤起学生强烈的探求欲望，也能带来学生间默契的配合与研究，激发他们不断的思考和创新，为培养新一代研究型人才做准备。]                 附教学流程图（见下页）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com