2017-2018学年安徽省滁州市定远县育才学校高二（普通班）下学期第三次月考数学（文）试题（Word版）

2017-2018学年安徽省滁州市定远县育才学校高二（普通班）下学期第三次月考数学（文）试题（Word版）

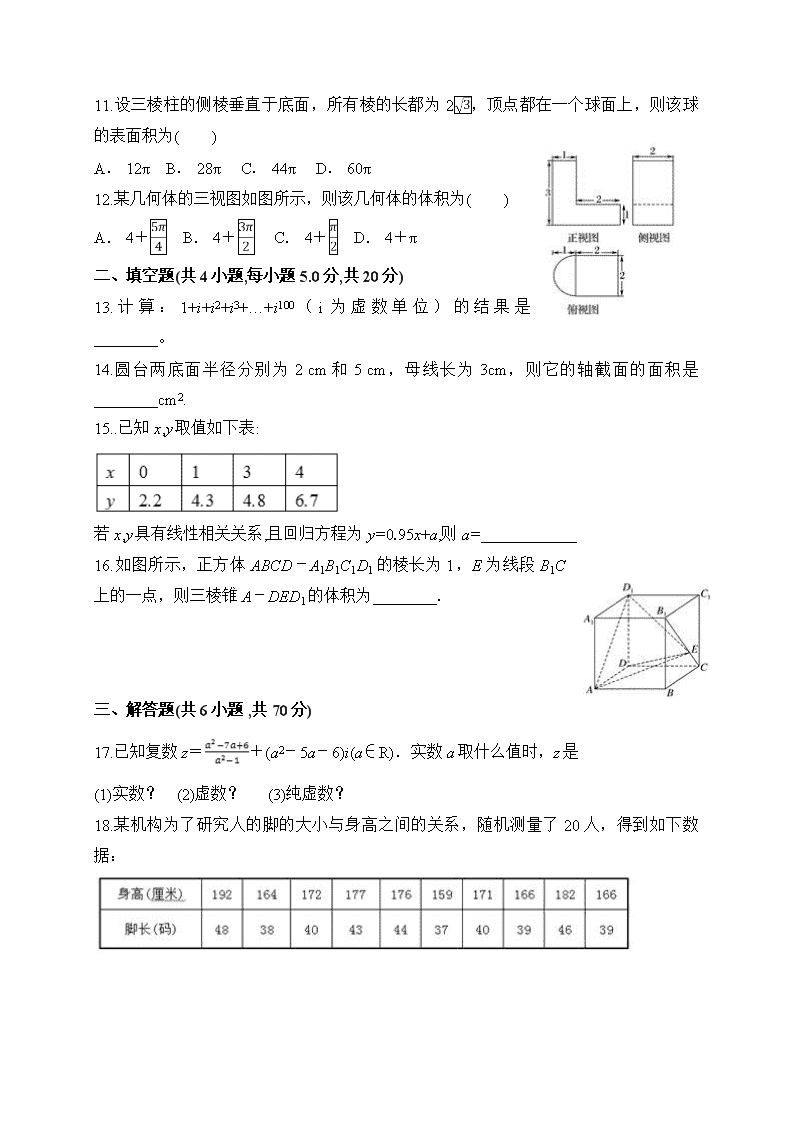
定远育才学校2017-2018学年度第二学期第三次月考试卷 高二文科（普通班）数学 ‎（本卷满分：150分，时间：120分钟，） 出卷人： ‎ 一、选择题(共12小题,每小题5分,共60分) ‎ ‎1.是虚数单位，i2013=（　　）‎ A． B． C．1 D．﹣1‎ ‎2.在判断两个变量与是否相关时，选择了4个不同的模型，它们的相关指数分别为：模型1的相关指数为0.98，模型2的相关指数为0.80，模型3的相关指数为0.50，模型4的相关指数为0.25.其中拟合效果最好的模型是 (　　)．‎ A．模型1 B．模型‎2 C．模型3 D．模型4‎ ‎3.为了解高中生作文成绩与课外阅读量之间的关系，某研究机构随机抽取了60名高中生，通过问卷调查，得到以下数据：‎ 由以上数据，计算得到K2的观测值k≈9.643，根据临界值表，以下说法正确的是(　　)‎ A．没有充足的理由认为课外阅读量大与作文成绩优秀有关 B．有0.5%的把握认为课外阅读量大与作文成绩优秀有关 C．有99.9%的把握认为课外阅读量大与作文成绩优秀有关 D．有99.5%的把握认为课外阅读量大与作文成绩优秀有关 ‎4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:‎ ‎ 由 列联表算得参照附表,得到的正确结论是(　　).‎ A．在犯错误的概率不超过的前提下认为“爱好该项运动与性别有关” ‎ ‎ B．在犯错误的概率不超过的前提下认为“爱好该项运动与性别无关”‎ C．在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”‎ D．在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”‎ ‎5.以下命题：‎ ‎①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥；‎ ‎②以直角梯形的一腰为轴旋转一周所得的旋转体是圆台；‎ ‎③圆柱、圆锥、圆台的底面都是圆；‎ ‎④一个平面截圆锥，得到一个圆锥和一个圆台．‎ 其中正确命题的个数为(　　)‎ A． 0 B． ‎1 C． 2 D． 3[]‎ ‎6. 将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为(　　)‎ A． 2π B． 4π C． 8π D． 16π ‎7. 平行四边形ABCD中，点A，B，C分别对应复数4＋i,3＋4i,3－5i，则点D对应的复数是(　　)‎ A．2－3i　 　 B．4＋8i C．4－8i　 　 D．1＋4i ‎8. 长方体的长、宽、高分别为4,2,2，其顶点都在一个球面上，则该球的表面积为(　　)‎ A． 12π B． 24π C． 48π D． 96π ‎9. 将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧视图为 (　　)‎ ‎ 　‎ A． 选项A B ． 选项B C． 选项C D． 选项D ‎10. 某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为(　　)‎ A． 80＋5π B． 80＋10π C ． 92＋14π D． 120＋10π ‎11.设三棱柱的侧棱垂直于底面，所有棱的长都为2，顶点都在一个球面上，则该球的表面积为(　　)‎ A． 12π B． 28π C． 44π D． 60π ‎12.某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A． 4＋ B． 4＋ C． 4＋ D． 4＋π 二、填空题(共4小题,每小题5.0分,共20分) ‎ ‎13.计算：1+i+i2+i3+…+i100（i为虚数单位）的结果是________。‎ ‎14.圆台两底面半径分别为‎2 cm和‎5 cm，母线长为‎3‎cm，则它的轴截面的面积是________cm2.‎ ‎15..已知x,y取值如下表:‎ 若x,y具有线性相关关系,且回归方程为y=0.95x+a,则a=____________‎ ‎16.如图所示，正方体ABCD－A1B‎1C1D1的棱长为1，E为线段B‎1C上的一点，则三棱锥A－DED1的体积为________．‎ 三、解答题(共6小题 ,共70分) ‎ ‎17.已知复数z＝＋(a2－‎5a－6)i(a∈R)．实数a取什么值时，z是 ‎(1)实数？ (2)虚数？ (3)纯虚数？‎ ‎18.某机构为了研究人的脚的大小与身高之间的关系，随机测量了20人，得到如下数据：‎ ‎(1) 若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为 “非高个”；“脚长大于‎42码”的为“大脚”，“脚长小于等于‎42码”的为“非大脚”，请根据上表数据完成下面的2×2列联表.‎ n=.‎ ‎(2)根据(1)中的2×2列联表，在犯错误的概率不超过0.01的前提下，能否认为脚的大小与身高之间有关系？‎ ‎19.一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：‎ 其中=1,2,3,4,5,6,7.‎ ‎(1)以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；‎ ‎(2)求线性回归方程；(结果保留到小数点后两位)‎ ‎(参考数据：=3 245,=25,=15.43,=5 075)‎ ‎(3)预测进店人数为80人时，商品销售的件数．(结果保留整数)‎ ‎20.三个图中，左面的是一个长方体截去一个角所得多面体的直观图，右面是它的正视图和侧视图.(单位：cm)‎ ‎(1)画出该多面体的俯视图；‎ ‎(2)按照给出的尺寸，求该多面体的体积.‎ ‎21.如图，已知点P在圆柱OO1的底面圆O上，AB为圆O的直径，圆柱的侧面积为16π，OA＝2，∠AOP＝120°，试求三棱锥A1－APB的体积.‎ ‎22.如图，一个圆锥的底面半径为1，高为3，在圆锥中有一个半径为x的内接圆柱.‎ ‎(1)试用x表示圆柱的高；‎ ‎(2)当x为何值时，圆柱的侧面积最大，最大侧面积是多少？‎ 答案解析 ‎1.【答案】A ‎2.【答案】A ‎3.【答案】D ‎4.【答案】A ‎5b ‎6.b ‎7c 8b 9b 10b 11.b 12.b ‎13.【答案】1‎ ‎14.【答案】63‎ ‎【解析】‎ 画出轴截面，‎ 如图，过A作AM⊥BC于M，‎ 则BM＝5－2＝3(cm)，‎ AM＝＝9(cm)，‎ 所以S四边形ABCD＝＝63(cm2)．‎ ‎15.【解析】由已知=2,=4.5,而回归方程过点,则4.5=0.95×2+a,∴a=2.6.‎ ‎16. 【解析】将三棱锥A-DED1选择△ADD1为底面，E为顶点，则V A-DED1=V E-ADD1，其中S△ADD1=SA1D1DA=，E到底面ADD1的距离等于棱长1， 故． 故答案为：‎ ‎17.【答案】(1)a＝6‎ ‎(2)a∈(－∞，－1)∪(－1,1)∪(1,6)∪(6，＋∞)时，z为虚数 ‎(3)不存在 ‎【解析】(1)当z为实数时，则有 所以 所以当时，z为实数．‎ ‎(2)当z为虚数时，则有 所以 即a≠±1且a≠6.‎ 所以当a∈(－∞，－1)∪(－1,1)∪(1,6)∪(6，＋∞)时，z为虚数．‎ ‎(3)当z为纯虚数时，则有 所以 所以不存在实数a使得z为纯虚数．‎ ‎18.【答案】(2) 有99%的把握认为脚的大小与身高之间有关系 ‎【解析】(1)‎ ‎(2)据2×2列联表可得χ2=≈8.802.‎ ‎∵8.802＞6.635,‎ ‎∴有99%的把握认为脚的大小与身高之间有关系.‎ ‎19.【答案】(2)(3) 58[]‎ ‎【解析】(1)散点图如图.‎ ‎(2)∵,‎ ‎=5 075,7()2=4 375,‎ ‎∴b=≈‎ ‎=‎ 故线性回归方程为 ‎(3)当时，(件)‎ 即进店人数为80人时，商品销售的件数约为58件.‎ ‎20 【解析】(1)作出俯视图如下.‎ ‎(2)所求多面体的体积V＝V长方体－V正三棱锥＝4×4×6－×(×2×2)×2＝(cm3).‎ ‎21. 【解析】‎ S圆柱侧＝2π·OA·AA1＝4π·AA1＝16π，∴AA1＝4，‎ ‎∵∠AOP＝120°，OA＝OP＝2，‎ ‎∴AP＝2，BP＝AB＝OA＝2.‎ ‎∴VA1－APB＝S△APB·AA1＝××2×2×4＝.‎ ‎22. 【解析】(1)设所求的圆柱的底面半径为x，它的轴截面如图，‎ BO＝1，PO＝3，圆柱的高为h，‎ 由图，得＝，即h＝3－3x.‎ ‎(2)∵S圆柱侧＝2πhx＝2π(3－3x)x＝6π(x－x2)，‎ 当x＝时，圆柱的侧面积取得最大值为π.‎ ‎∴当圆柱的底面半径为时，它的侧面积最大为π.‎