2021新高考2版数学一轮讲义：第一章 第二节　命题及其关系充分条件与必要条件

2021新高考2版数学一轮讲义：第一章 第二节　命题及其关系充分条件与必要条件

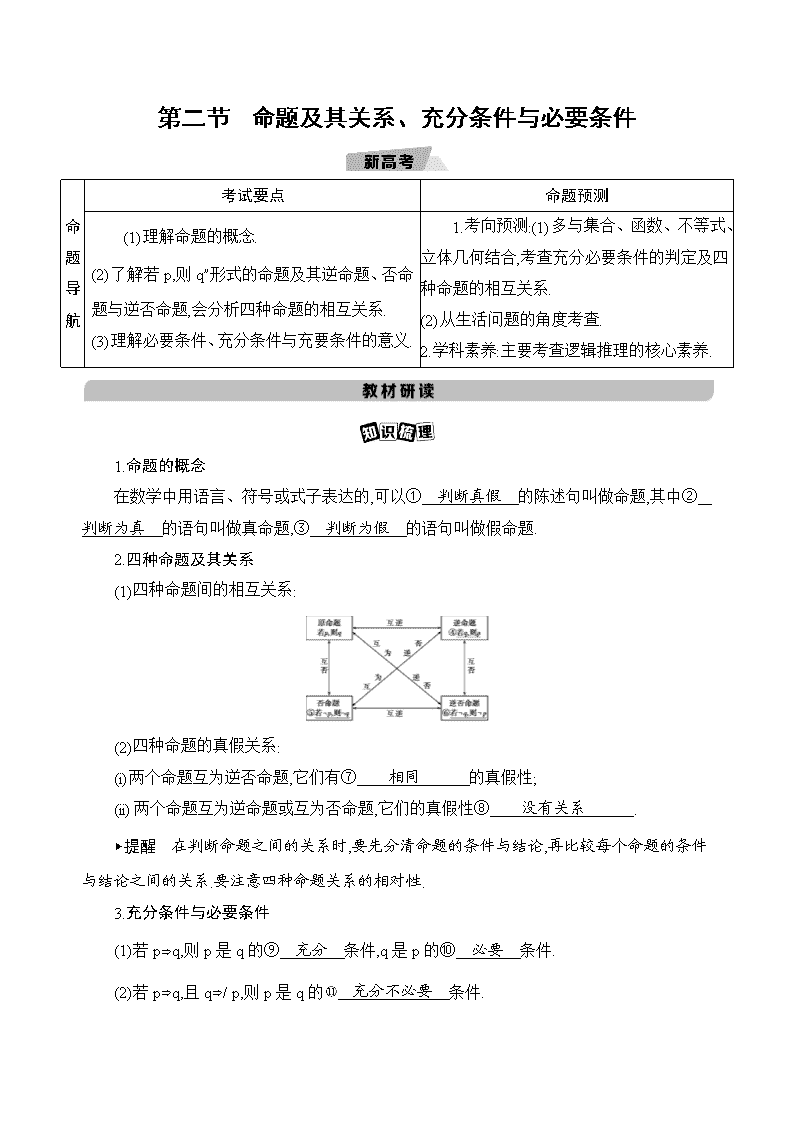
第二节　命题及其关系、充分条件与必要条件 命题导航 考试要点 命题预测 ‎　　(1)理解命题的概念.‎ ‎(2)了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.‎ ‎(3)理解必要条件、充分条件与充要条件的意义.‎ ‎　　1.考向预测:(1)多与集合、函数、不等式、立体几何结合,考查充分必要条件的判定及四种命题的相互关系.‎ ‎(2)从生活问题的角度考查.‎ ‎2.学科素养:主要考查逻辑推理的核心素养.‎ ‎　　1.命题的概念 在数学中用语言、符号或式子表达的,可以①　判断真假　的陈述句叫做命题,其中②　判断为真　的语句叫做真命题,③　判断为假　的语句叫做假命题. ‎ ‎2.四种命题及其关系 ‎(1)四种命题间的相互关系:‎ ‎(2)四种命题的真假关系:‎ ‎(i)两个命题互为逆否命题,它们有⑦　　相同　　　的真假性; ‎ ‎(ii)两个命题互为逆命题或互为否命题,它们的真假性⑧　　没有关系　　　. ‎ ‎▶提醒　在判断命题之间的关系时,要先分清命题的条件与结论,再比较每个命题的条件与结论之间的关系.要注意四种命题关系的相对性.‎ ‎3.充分条件与必要条件 ‎(1)若p⇒q,则p是q的⑨　充分　条件,q是p的⑩　必要　条件. ‎ ‎(2)若p⇒q,且q⇒/ p,则p是q的　充分不必要　条件. ‎ ‎(3)若p⇒/ q,且q⇒p,则p是q的　必要不充分　条件. ‎ ‎(4)若p⇔q,则p是q的　充要　条件. ‎ ‎(5)若p⇒/ q,且q⇒/ p,则p是q的　既不充分也不必要　条件. ‎ ‎▶提醒　不能将“若p,则q”与“p⇒q”混为一谈,只有“若p,则q”为真命题时,才有“p⇒q”.‎ 知识拓展 ‎　　(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的充分不必要条件;‎ ‎(2)若p是q的充分不必要条件,则¬q是¬p的充分不必要条件.‎ ‎1.判断正误(正确的打“√”,错误的打“✕”).‎ ‎(1)“x2-3x+2=0”是命题.(✕)‎ ‎(2)一个命题的逆命题与否命题,它们的真假没有关系.(✕)‎ ‎(3)命题“若p不成立,则q不成立”等价于“若q成立,则p成立”.(√)‎ ‎(4)若p是q成立的充分条件,则q是p成立的必要条件.(√)‎ ‎(5)命题“若p,则q”的否命题是“若p,则¬q”.(✕)‎ ‎(6)一个命题非真即假.(√)‎ ‎2.下列命题的逆命题为真命题的是(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.若x>2,则(x-2)(x+1)>0‎ B.若x2+y2≥4,则xy=2‎ C.若x+y=2,则xy≤1‎ D.若a≥b,则ac2≥bc2‎ 答案　B ‎3.当命题“若p,则q”为真时,下列命题中一定为真的是(　　)‎ A.若q,则p ‎ B.若¬p,则¬q ‎ C.若¬q,则¬p ‎ D.若p,则¬q ‎ 答案　C ‎4.若x∈R,则“x>1”是“‎1‎x<1”的(　　)‎ A.充分不必要条件 ‎ B.必要不充分条件 C.充要条件 ‎ D.既不充分也不必要条件 答案　A ‎5.已知p:x>1或x<-3,q:x>a,若q是p的充分不必要条件,则a的取值范围是(　　)‎ A.[1,+∞) ‎ B.(-∞,1]‎ C.[-3,+∞) ‎ D.(-∞,-3)‎ 答案　A 命题及其相互关系 典例1　(1)命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是(　　)‎ A.若x+y是偶数,则x与y不都是偶数 B.若x+y是偶数,则x与y都不是偶数 C.若x+y不是偶数,则x与y不都是偶数 D.若x+y不是偶数,则x与y都不是偶数 ‎(2)给定下列命题:‎ ‎①若k>0,则方程x2+2x-k=0有实数根;‎ ‎②“若a>b,则a+c>b+c”的否命题;‎ ‎③“矩形的对角线相等”的逆命题;‎ ‎④“若xy=0,则x,y中至少有一个为0”的否命题;‎ ‎⑤“若x≠2或y≠3,则x+y≠5”.‎ 其中真命题的序号是　　　　　. ‎ 答案　(1)C　(2)①②‎ 方法技巧 ‎　　1.写一个命题的其他三种命题时,需注意:‎ ‎(1)对于不是“若p,则q”形式的命题,需先改写成“若p,则q ”的形式;‎ ‎(2)若命题有大前提,则写其他三种命题时须保留大前提.‎ ‎2.判断一个命题为真命题,要给出推理证明;判断一个命题是假命题,只需举出反例.‎ ‎3.当一个命题直接判断不易进行时,根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,可将命题转化为等价命题,再判断真假.‎ ‎　　1-1　命题“若x2<1,则-11或x<-1,则x2>1‎ D.若x≥1或x≤-1,则x2≥1‎ 答案　D ‎1-2　下列命题中为真命题的是(　　)‎ A.命题“若x>y,则x>|y|”的逆命题 B.命题“x>1,则x2>1”的否命题 C.命题“若x=1,则x2+x-2=0”的否命题 D.命题“若x2>0,则x>1”的逆否命题 答案　A 充分条件、必要条件的判断 典例2　(1)设x∈R,则“2-x≥0”是“|x-1|≤1”的(　　)‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎(2)给定两个命题p,q,若¬p是q的必要不充分条件,则p是¬q的(　　)‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案　(1)B　(2)A 方法技巧 ‎　　判断充要条件的常用方法 ‎(1)定义法:根据p⇒q,q⇒p进行判断.‎ ‎(2)集合法:根据p,q成立的对应的集合之间的包含关系进行判断.‎ ‎(3)等价转化法:根据一个命题与其逆否命题的等价性,把需判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题.‎ ‎　　2-1　已知p:x2-3x+2>0,q:‎1‎x‎2‎‎-5x+4‎>0,则p是q的　　　　条件;¬q是¬p的　　　　条件;¬p是¬q的　　　　条件. ‎ 答案　必要不充分;必要不充分;充分不必要 ‎2-2　集合A={x|x>1},B={x|x<2},则“x∈A或x∈B”是“x∈(A∩B)”的　　　　　　　条件. ‎ 答案　必要不充分 充分条件、必要条件的应用 典例3　(1)设α:1≤x≤3,β:m+1≤x≤2m+4,m∈R,若α是β的充分条件,则m的取值范围是　　　　. ‎ ‎(2)已知条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0.若¬p是¬q的必要不充分条件,则实数a的取值范围是　　　　. ‎ 答案　(1)‎‎-‎1‎‎2‎,0‎ ‎(2)‎0,‎‎1‎‎2‎　‎ 解析　(1)若α是β的充分条件,则α对应的集合是β对应集合的子集,则m+1≤1,‎‎2m+4≥3,‎ 解得-‎1‎‎2‎≤m≤0.‎ ‎(2)由2x2-3x+1≤0,得‎1‎‎2‎≤x≤1,设条件p对应的集合为P,则P=x|‎1‎‎2‎≤x≤1‎.‎ 由x2-(2a+1)x+a(a+1)≤0,得a≤x≤a+1,设条件q对应的集合为Q,则Q={x|a≤x≤a+1}.‎ ‎∵¬p是¬q的必要不充分条件,∴q是p的必要不充分条件,‎ ‎∴P⫋Q,∴0≤a≤‎1‎‎2‎,‎ ‎∴实数a的取值范围是‎0,‎‎1‎‎2‎.‎ 方法技巧 ‎　　1.解题“2关键”:‎ ‎(1)把充分、必要条件转化为集合之间的关系.‎ ‎(2)根据集合之间的关系列出关于参数的不等式(组)求解.‎ ‎　　2.解题“1注意”:‎ 求参数的取值范围时,一定要注意区间端点值的检验,尤其是利用两个集合之间的关系求参数的取值范围时,不等式能否取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.‎ ‎　　3-1　已知命题p:“关于x的方程x2-4x+a=0有实根”,若¬p是真命题的充分不必要条件为a>3m+1,则实数m的取值范围是(　　)‎ A.[1,+∞) B.(1,+∞) C.(-∞,1) D.(-∞,1]‎ 答案　B ‎　　3-2　已知p:A={x|x2-2x-3≤0},q:B={x|x2-2mx+m2-4≤0,m∈R}.若p是¬q的充分条件,则实数m的取值范围是　　　　　　　. ‎ 答案　(-∞,-3)∪(5,+∞)‎ 解析　易知A={x|-1≤x≤3},B={x|m-2≤x≤m+2},‎ ‎∴∁RB={x|xm+2}.‎ ‎∵p是¬q的充分条件,‎ ‎∴A⊆∁RB,‎ ‎∴m-2>3或m+2<-1,∴m>5或m<-3.‎ ‎1.命题“若x≥a2+b2,则x≥2ab”的逆命题是(　　)　　　　　　 　　　　　　 　　　　　　 ‎ A.若x3的一个充分不必要条件是(　　)‎ A.x>2 B.x>4‎ C.x<4 D.x<2‎ 答案　B ‎3.下列说法正确的是(　　)‎ A.“x<2”是“x<4”是必要条件 B.“xy=0”是“y=0”的充分条件 C.“x=0”是“x2+y2=0”的必要条件 D.“|x|<1”是“x<1”的充要条件 答案　C ‎4.下列结论错误的是(　　)‎ A.命题“若x2-3x-4=0,则x=4”的逆否命题是“若x≠4,则x2-3x-4≠0”‎ B.命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题 C.“x=4”是“x2-3x-4=0”的充分条件 D.命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”‎ 答案　B ‎5.已知命题α:如果x<3,那么x<5;命题β:如果x≥3,那么x≥5;命题γ:如果x≥5,那么x≥3.关于这三个命题之间的关系,下列三种说法正确的是(　　)‎ ‎①命题α是命题β的否命题,且命题γ是命题β的逆命题;‎ ‎②命题α是命题β的逆命题,且命题γ是命题β的否命题;‎ ‎③命题β是命题α的否命题,且命题γ是命题α的逆否命题.‎ A.①③ B.② C.②③ D.①②③‎ 答案　A ‎6.已知p:x+y≠-2,q:x,y不都是-1,则p是q的(　　)‎ A.充分不必要条件 ‎ B.必要不充分条件 C.充要条件 ‎ D.既不充分也不必要条件 答案　A　因为p:x+y≠-2,q:x≠-1或y≠-1,‎ 所以¬p:x+y=-2,¬q:x=-1且y=-1,‎ 易知¬q⇒¬p,但¬p⇒/ ¬q,所以¬q是¬p的充分不必要条件,即p是q的充分不必要条件.‎ ‎7.函数f(x)=log‎2‎x,x>0,‎‎-‎2‎x+a,x≤0‎有且只有一个零点的充分不必要条件是(　　)‎ A.a<0 B.01‎ 答案　A ‎8.圆x2+y2=1与直线y=kx-3有公共点的充分不必要条件是(　　)‎ A.k≤-2‎2‎或k≥2‎2‎ B.k≤-2‎‎2‎ C.k≥2 D.k≤-2‎2‎或k>2‎ 答案　B　若直线与圆有公共点,则圆心(0,0)到直线kx-y-3=0的距离d=‎|-3|‎k‎2‎‎+1‎≤1,即k‎2‎‎+1‎≥3,∴k2+1≥9,即k2≥8,∴k≥2‎2‎或k≤-2‎2‎,∴由选项知圆x2+y2=1与直线y=kx-3有公共点的充分不必要的条件是k≤-2‎2‎,故选B.‎ ‎9.已知条件p:|x-4|≤6;条件q:(x-1)2-m2≤0(m>0),若p是q的充分不必要条件,则m的取值范围是(　　)‎ A.[21,+∞) B.[9,+∞)‎ C.[19,+∞) D.(0,+∞)‎ 答案　B　条件p:-2≤x≤10,条件q:1-m≤x≤m+1,又p是q的充分不必要条件,故有‎1-m≤-2,‎‎1+m≥10,‎m>0,‎解得m≥9.‎ ‎10.已知命题“若a0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数”是真命题;‎ ‎②命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”;‎ ‎③命题“若x,y都是偶数,则x+y也是偶数”的逆命题为真命题;‎ ‎④命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”等价.‎ 答案　②④‎ ‎12.设有非空集合A、B、C,若“a∈A”的充要条件是“a∈B且a∈C”,则“a∈B”是“a∈A”的　　　　　　　　条件.  ‎ 答案　必要不充分 ‎13.若“x2>1”是“x3,即m>2.‎ ‎17.某天,小赵、小张、小李、小刘四人一起到电影院看电影,他们到达电影院之后发现,当天正在放映A,B,C,D,E五部影片,于是他们商量一起看其中的一部影片.‎ 小赵说:只要不是B就行;‎ 小张说:B,C,D,E都行;‎ 小李说:我喜欢D,但是只要不是C就行;‎ 小刘说:除了E之外,其他的都可以.‎ 据此判断,他们四人可以共同看的影片为　　　　. ‎ 答案　D 解析　小赵可以看的电影的集合为{A,C,D,E},小张可以看的电影的集合为{B,C,D,E},小李可以看的电影的集合为{A,B,D,E},小刘可以看的电影的集合为{A,B,C,D},这四个集合的交集中只有元素D,故填D.‎