2020-2021年新高三数学一轮复习考点 二次函数与幂函数

2020-2021年新高三数学一轮复习考点 二次函数与幂函数

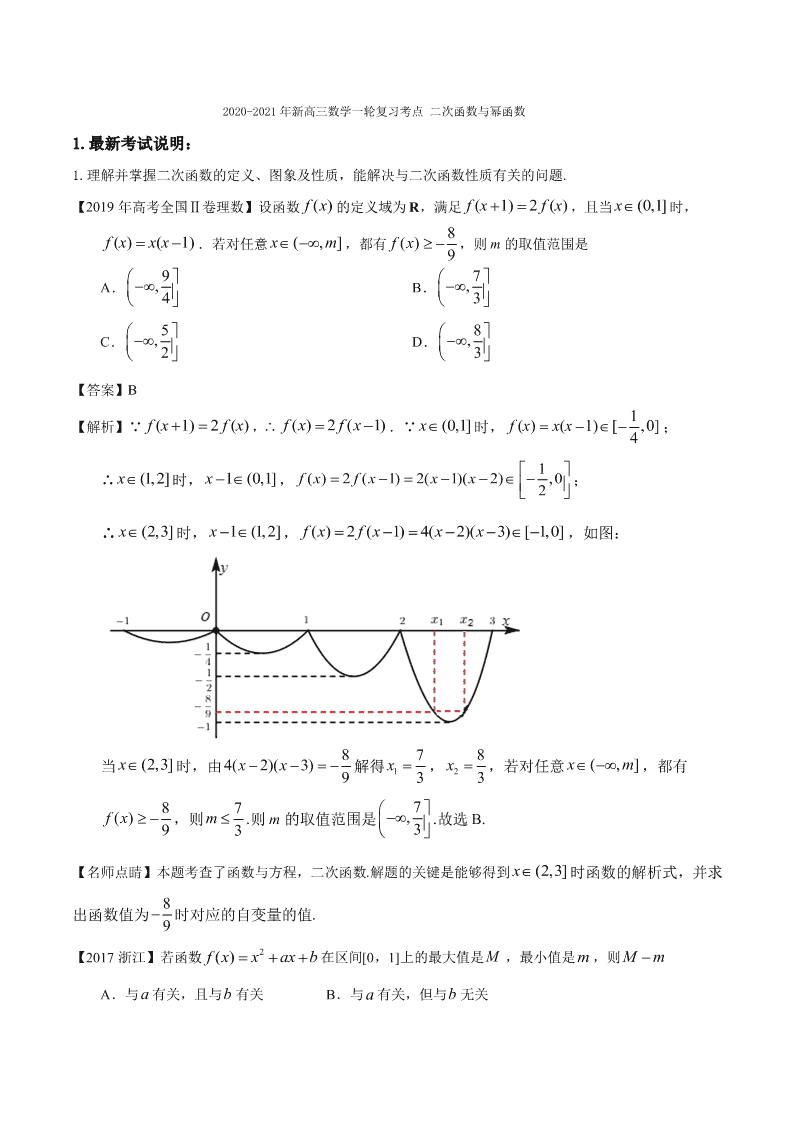
2020-2021 年新高三数学一轮复习考点 二次函数与幂函数 1.最新考试说明： 1.理解并掌握二次函数的定义、图象及性质，能解决与二次函数性质有关的问题. 【2019 年高考全国Ⅱ卷理数】设函数 ()fx的定义域为 R，满足 ( 1 ) 2 ( )f x f x ，且当 ( 0 ,1]x  时， ( ) ( 1 )f x x x ．若对任意 ( , ]xm   ，都有 8() 9fx ，则 m 的取值范围是 A． 9, 4   B． 7, 3   C． 5, 2   D． 8, 3   【答案】B 【解析】∵ ( 1 ) 2 ( )f x f x ， ()2(1)fxfx ．∵ 时， 1()(1)[,0] 4fxxx  ； ∴ (1,2 ]x  时， 1 ( 0 ,1]x  ， 1()2(1)2(1)(2),0 2fxfxxx   ； ∴ (2,3]x  时， 1(1,2]x ， ( )2(1)4(2)(3)[ 1,0]fxfxxx  ，如图： 当 时，由 84(2)(3) 9xx  解得 1 7 3x  ， 2 8 3x  ，若对任意 ，都有 ，则 7 3m  .则 m 的取值范围是 .故选 B. 【名师点睛】本题考查了函数与方程，二次函数.解题的关键是能够得到 时函数的解析式，并求 出函数值为 8 9 时对应的自变量的值. 【2017 浙江】若函数 2()f x x ax b   在区间[0，1]上的最大值是 M ，最小值是 m ，则 Mm A．与 a 有关，且与b 有关 B．与 有关，但与 无关 C．与 a 无关，且与 b 无关 D．与 无关，但与 有关 【答案】B 【解析】函数 ()fx的对称轴为 2 ax  ， ①当 02 a ≤ ，此时 (1)1Mfab ， ( 0 )m f b， 1M m a   ； ②当 12 a ≥ ，此时 ( 0 )M f b， (1)1mfab ， 1M m a    ； ③当012 a   ，此时 2 ()24 aamfb ， (0)M f b或 (1) 1M f a b    ， 2 4 aMm 或 2 1 4 aMma ．综上， Mm 的值与 a 有关，与 b 无关．选 B。 2.结合函数 y＝x，y＝x2，y＝x3，y＝x 1 2 ， 1y= x 的图象，了解它们的变化情况． 【2020 年高考上海卷 11】已知 aR ，若存在定义域为 R 的函数 ()fx同时满足下列两个条件，①对任意 0xR ， 0()fx 的值为 0x 或 0 2x ；②关于 x 的方程 ()f x a 无实数解；则 a 的取值范围为 ． 【答案】     ,00,11, 【解析】由 2yx 和 yx 的图象和函数的定义可知，若满足  0fx 的值为 0x 或   2 00fxx  ，只有   2000f  ，   2111f  ，结合②可知若方程  fxa  无实数解，则 a  ， 故答案为： ． 【专家解读】本题的特点是函数图象及其性质的应用，本题考查了函数与方程，二次函数图象及其应用， 考查函数与方程思想、数形结合思想，考查数学运算、数学直观、数学建模等学科素养．解题关键是正确 作出函数图象，应用函数图象及其性质解决问题． 【2020 年高考江苏卷 7】已知 ()y f x 是奇函数，当 0x  时， 2 3()f x x ，则 ( 8)f  的值是 ． 【答案】 4 【解析】 ()y f x 是奇函数，当 0x  时， 2 3()f x x  ，则 2 3(8)(8)84ff ． 【专家解读】本题考查了函数的奇偶性，考查数学运算学科素养．解题关键是正确应用函数的奇偶性． 2.命题方向预测： 1.关于幂函数常以 5 种幂函数为载体，考查幂函数的概念、图象与性质，多以小题形式出现，属容易题． 2.二次函数的图象及性质是近几年高考的热点；用三个“二次”间的联系解决问题是重点，也是难点． 3.题型以选择题和填空题为主，若与其他知识点交汇，则以解答题的形式出现. 3.课本结论总结： 二次函数与幂函数 1．二次函数 (1)二次函数解析式的三种形式 ①一般式：f(x)＝ax2＋bx＋c(a≠0)． ②顶点式：f(x)＝a(x－m)2＋n(a≠0)． ③零点式：f(x)＝a(x－x1)(x－x2)(a≠0)． (2)二次函数的图象和性质 解析式 f(x)＝ax2＋bx＋c(a>0) f(x)＝ax2＋bx＋c(a<0) 图象 定义域 (－∞，＋∞) (－∞，＋∞) 值域 24 4 ac b a   ， 24 4 ac b a   ， 单调性 在 x∈ 2 b a   ，- 上单调递减； 在 x∈ 2 b a    ， 上单调递增 在 x∈ 2 b a    ， 上单调递减在 x∈ 2 b a   ，- 上单调递增 对称性 函数的图象关于 x＝ 2 b a 对称 2.幂函数 (1)定义：形如 y＝xα(α∈R)的函数称为幂函数，其中 x 是自变量，α 是常数． (2)幂函数的图象比较 (3)幂函数的性质比较 特征 函数 性质 y＝x y＝x2 y＝x3 1 2yx y＝x－1 定义域 R R R [0，＋ ∞) {x|x∈R 且 x≠0} 值域 R [0，＋∞) R [0，＋ ∞) {y|y∈R 且 y≠0} 奇偶性 奇函数 偶函数 奇函数 非奇非偶 函数 奇函数 单调性 增 x∈[0，＋ ∞) 时，增； x∈(－∞，0] 时，减 增 增 x∈(0，＋∞) 时， 减；x∈(－∞，0) 时，减 4.名师二级结论： （1）二次函数图象对称轴的判断方法 (i)二次函数 y＝f(x)对定义域内所有 x，都有 f(x1)＝f(x2)，那么函数 y＝f(x)的图象关于 x＝x1＋x2 2 对称。 (ii)二次函数 y＝f(x)对定义域内所有 x，都有 f(a＋x)＝f(a－x)成立的充要条件是函数 y＝f(x)的图象关于 直线 x＝a 对称(a 为常数)。 (2 幂函数 y＝xα 在第一象限的图象特征 (i)α>1 时，图象过(0,0)，(1,1)，下凸递增，例如 y＝x3。 (ii)0<α<1 时，图象过(0,0)，(1,1)，上凸递增，例如 y＝x 1 2 。 (iii)α<0 时，图象过(1,1)，下凸递减，且以两条坐标轴为渐近线，例如 y＝x－1。 (3)一元二次不等式恒成立的条件 (i)ax2＋bx＋c>0(a≠0)恒成立的充要条件是   a>0， Δ<0。 (ii)ax2＋bx＋c<0(a≠0)恒成立的充要条件是   a<0， Δ<0。 5.课本经典习题： (1)新课标 A 版第 70 页，B 组第 2 题 指数函数 xby a   的图象如图所示，求二次函数 2y ax bx的顶点的横坐标的取值范围． 【解析】由图可知指数函数 xby a   是减函数，所以 01b a．而二次函数 2y ax bx的顶点的横坐标 为 1 22 bb aa    ，所以 1 022 b a    ，即二次函数 2y a x b x的顶点的横坐标的取值范围是 1 02  ， ． 【经典理由】有效把指数函数和二次函数相结合 (2)新课标 A 版第 822 页，A 组第 10 题 已知幂函数 ()yfx 的图象过点 22 2 （ ， ），试求出此函数的解析式，并作出图像，判断奇偶性、单调性． 【分析】根据幂函数的概念设 () nf x x  ，将点的坐标代入即可求得 n 值，从而求得函数解析式．要判断函 数的奇偶性我们可以根据函数奇偶性的定义判断函数的奇偶性，判断函数图象在（0，+∞）的单调性，进 而画出函数的图象． 【解析】设 ,因为幂函数 22 2 （ ， ）, 212,22 n n  ， 这个函数解析式为 1 2yx  ．定义域为（0，+∞），它不关于原点对称，所以，y=f（x）是非奇非偶函数． 当 x＞0 时，f（x）是单调减函数，函数的图象如图． 【经典理由】本题通过待定系数法求幂函数解析式、解指数方程的解法、奇（偶）函数性、幂函数图象考 查学生对幂函数有关知识的掌握程度和对知识的综合应用能力 6.考点交汇展示： (1)二次函数与概率交汇 例 1.在区间 6,9 内任取一个实数 m ，设   2fxxmxm  ，则函数  fx的图像与 x 轴有公共点的 概率等于（） A． 8 15 B． 3 5 C． 2 3 D． 11 15 【答案】D 【解析】∵f（x）＝﹣x2+mx+m 的图象与 x 轴有公共点，∴△＝m2+4m  0，∴m  ﹣4 或 m 0， ∴在[﹣6，9]内任取一个实数 m，函数 f（x）的图象与 x 轴有公共点的概率等于 4690 11 9615   ． (2)二次函数与三角函数交汇 例 2．若函数 ()sin24sinfxxxmx 在 [ 0 ,2 π ] 上单调递减，则实数 m 的取值范围为（ ） A． ( 2 ,2 ) B． [ 2 ,2 ] C． ( 1,1) D．[ 1,1] 【答案】B 【解析】依题意， ()2sincos4sinsin 24sinfxxxxmxxxmx ，所以 22()2(2cos1)4cos4coscos60fxxmxxmx  对 [0,2π]x 恒成立.设 c o s [ 1 ,1 ]tx   ， 2()46gttmt ，则 ( ) 0gt  在 上恒成立，由二次函数图象得 ( 1 ) 0 , ( 1 ) 0 , g g    即 4 6 0 4 6 0 m m        ， 解得 22m   .故选：B. (3)二次函数与平面向量交汇 例 3．已知圆 O 的半径为 2， P ,Q 是圆 上任意两点，且 POQ60  ， AB 是圆 的一条直径，若点 C 满足  1OC OPOQ （ λ R ），则 CA CB 的最小值为（ ） A．-1 B．-2 C．-3 D．-4 【答案】C 【解析】因为      2 · · ·       CO OA CO OB CO CO OA OB OA OBCA CB ，由于圆 的半径为 2 ， AB 是圆 的一条直径，所以 0OAOB，  2214 OAOB ，又 60POQ  ，所以   22 · 4 1 4     CA CB CO OP OQ ，    222 2· 121? · · 4CA CBOPOP OQOQ ·CACB    224 3 3 1 4 4 3 3         21343 24    ，所以，当 1 2  时， 21333 244 min    ，故 的最小值为 3434   ，故选 C． (4)幂函数与函数奇偶性交汇 例 4．下列函数既是偶函数，又在 0,  上单调递增的是（ ） A． 1 2y x B． 2yx-= C． 3yx D． 4yx 【答案】D 【解析】A 选项，函数 的定义域为  0,  ，所以函数 是非奇非偶函数，排除 A；B 选项，幂 函数 在  0,  上单调递减，排除 B；C 选项，函数 的定义域为 R ，   3 3xx   ，所以函数 是奇函数，排除 C；D 选项，函数 的定义域为 ，且   4 4xx，所以函数 是偶函数； 又由幂函数的性质可得，幂函数 在 上单调递增，故 D 正确； (5)二次函数与不等式交汇 例 5.【2017 天津，理 8】已知函数 2 3,1, () 2 ,1. xxx fx xxx     设 a  R ，若关于 x 的不等式 ( ) | | 2 xf x a  在 R 上恒成立，则 a 的取值范围是 （A） 47[ ,2 ]16 （B） 4 7 3 9[ , ] 1 6 1 6 （C） [ 2 3,2 ] （D） 39[ 2 3, ] 16 【答案】 A 222222 xx xx （当 2x  时取等号），所以 232 a ，综上 47 216 a   ．故选 A． 【考点分类】 热点 1 幂函数、 1．函数 4 3yx 的图像大致是（ ） A． B． C． D． 【答案】A 【解析】 4 3 43y x x ， 该函数的定义域为 R ，所以排除 C；因为函数为偶函数，所以排除 D； 又 4 13  ， 4 3yx 在第一象限内的图像与 2yx= 的图像类似，排除 B. 4．已知幂函数    37mfxxmN 的图象关于 y 轴对称，且与 x 轴、 轴均无交点，则 m 的值为（ ） A． 1 B．0 C．1 D．2 【答案】C 【解析】由题意可得：370m且 37m  为偶数， mN ， 解得 7 3m  ，且 为偶数， ， ∴ 1m  ． 故选：C． 3．若 0＜a＜b＜1，x＝ab，y＝ba，z＝bb，则 x、y、z 的大小关系为（ A．x＜z＜y B．y＜x＜z C．y＜z＜x D．z＜y＜x 【答案】A 【解析】因为 01ab ，故 () xfxb  单调递减；故 aby b z b   ，幂函数 () bgxx  单调递增； 故 bbx a z b   ，则 、 、 z 的大小关系为： xzy ；故选：A 热点 2 二次函数 1．若函数 2 43yxx  的定义域为  0, t ，值域为  3 ,1 ，则t 的取值范围是( ) A． 0, 4 B． 3 ,32   C． 2, D． 2, 4 【答案】D 【解析】如图 令   2 43y f x x x     ，则      0 3, 4 3, 2 1f f f     ，又定义域为  0, t ，值域为 3,1 所以  2 ,4t  ，故选：D 2.设函数 ln , 0() ( 1), 0x xxfx e x x     ，若方程 2 1[()()0 1] 6fxafx  有六个不等的实数根，则实数 a 可取 的值可能是（ ） A． 2 3 B． 或 1 C．1 D． 或 2 【答案】B 【解析】当 0x  时，    1xfxex ，则 ()(1)(2) xxxfxexeex  ，由   0fx  得 20x ， 即 2x  时，  fx单调递减，由   0fx  得 20x ，即 20x   时， 单调递增，当 2x  时， 取得极小值 2 1(2)f e ， (0 ) 1f  ，作出 的图象如图： 由图象可知当  01fx时，有三个不同的 x 与 对应，设  t f x ，方程 有六个不等的实数根，所以 2 1 016t at   在  0,1t  内有两个不等的实根，设 2 1() 16g ttat ， 所以 2 1 016(0)0 1(1)0 10117160 1 2164016012 012 g g a a aa a             ，则实数 a 可能是 2 3 或 1. 3. 已知函数 2( ) 1f x x m x   ，若对于任意的  ,1x m m都有 ( ) 0fx ，则实数 m 的取值范围 为 . 【答案】 2( ,0) 2 【解析】据题意 22 2 ()10, (1)(1)(1)10, fmmm fmmmm    解得 2 02 m   ． 【方法规律】 1.二次函数在闭区间上的最值与抛物线的开口方向、对称轴位置、闭区间三个要素有关； 2.常结合二次函数在该区间上的单调性或图象求解，在区间的端点或二次函数图象的顶点处取得最值.二次 函数、二次方程、二次不等式之间可以相互转化．一般规律(1)在研究一元二次方程根的分布问题时，常借 助于二次函数的图象数形结合来解，一般从①开口方向；②对称轴位置；③判别式；④端点函数值符号四 个方面分析．(2)在研究一元二次不等式的有关问题时，一般需借助于二次函数的图象、性质求解． 3.幂函数 y＝xα 的图象与性质由于 α 的值不同而比较复杂，一般从两个方面考查 (1)α 的正负：α>0 时，图象过原点和(1,1)，在第一象限的图象上升；α<0 时，图象不过原点，在第一 象 限的图象下降，反之也成立． (2)曲线在第一象限的凹凸性：α>1 时，曲线下凸；0<α<1 时，曲线上凸；α<0 时，曲线下凸． 4．二次函数、二次方程、二次不等式间相互转化的一般规律： (1)在研究一元二次方程根的分布问题时，常借助于二次函数的图象数形结合来解，一般从：①开口方向； ②对称轴位置；③判别式；④端点函数值符号四个方面分析． (2)在研究一元二次不等式的有关问题时，一般需借助于二次函数的图象、性质求解． 5．幂函数 y＝xα(α∈R)图象的特征 α>0 时，图象过原点和(1,1)，在第一象限的图象上升；α<0 时，图象不过原点，在第一象限的图象下降， 反之也成立． 【解题技巧】 1.做二次函数类型题是注意数形结合的应用，画出函数的草图能帮助我们理清思路 2.二次函数中如果含有参数，往往要进行分类讨论 3.对于函数 y＝ax2＋bx＋c，要认为它是二次函数，就必须满足 a≠0，当题目条件中未说明 a≠0 时，就要 讨论 a＝0 和 a≠0 两种情况． 4.幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内， 要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交 点一定是原点. 【易错点睛】 1.注意幂函数与指数函数的联系与区别 2.幂函数的增减与α的关系 3.对于函数 y＝ax2＋bx＋c，要认为它是二次函数，就必须满足 a≠0，当题目条件中未说明 a≠0 时，就要 讨论 a＝0 和 a≠0 两种情况． 例 如图是函数 m nyx (m、n∈N*，m、n 互质)的图象，则下列判断正确的是________． ①m、n 是奇数，且 m n ＜1 ②m 是偶数，n 是奇数且 m n ＞1 ③m 是偶数，n 是奇数且 m n ＜1 ④m 是奇数，n 是偶数且 m n ＞1 解析：将分数指数式化为根式 y= n mx ，由定义域为 R，值域为[0，＋∞)知 n 为奇数，m 为偶数，又由幂函 数 y＝xα，当 α＞1 时，图象在第一象限的部分下凸，当 0＜α＜1 时，图象在第一象限的部分上凸，故③ 正确．答案：③ 【易错点】幂函数的单调性和 a 有关，注意 a 与 0 和 1 的比较 【热点预测】 1．若 1 2( ) (log 1) mf x m x 为幂函数，则 ( 3 )f  （ ） A． 3 B． 3 3 C．9 D． 1 9 【答案】C 【解析】由题意 2log 1 1m， 1m  ，∴ 2()fxx  ，∴ (3)9f  ． 2．函数    2 231f xaxax 在区间 4, 上递增，则实数 a 的取值范围是（ ） A． 0,1 B． 0,1 C． ,1 D． 1,  【答案】A 【解析】当 0a  时，   61f x x 在区间  4,  上递增，满足条件；当 0a  时，若函数    2 231fxaxax 在区间 上递增，则   0 2342 a a a     ，解得  0 ,1a  ，综上所述，实 数 a 的取值范围是  0,1 ，故选 A. 3．若 1xy，则下列一定成立的是（ ） A． 11( ) ( )24 xy B． 11( ) ( )24 xy C． 11 24xy D． 11 24xy 【答案】C 【解析】因为 211()42   y y ，由 ，但并不清楚 ,2xy之间大小关系，所以 11( ) ,( )24 xy大小关系不明 确，则 A,B 不对，因为   11 24 yy，由 ，所以 xy，有 1 2y x 在  0,  单调递增，所以 ，故 C 正确，D 错误 4．已知函数  logayxb的大致图象如下图，则幂函数 b ayx 在第一象限的图象可能是（ ） A． B． C． D． 【答案】B 【解析】由  l o g ay x b的图象可知， 1 log (1 ) 0 log (2 ) 0 a a a b b      ，所以 1 0 1 1 21 a b b        ，得 1a  ， 01b， 所以 01b a，所以幂函数 b ayx 在第一象限的图象可能为 B . 5．满足 11 33(1)(32)mm  的实数 m 的取值范围是（ ）. A． 23,32   B． 23, 1,32            C． 2 ,3  D． 23(,1), 32   【答案】D 【解析】幂函数 1 3yx  在(0, ) 为减函数，且函数值为正，在( ,0) 为减函数，且函数值为负， 等价于 3 2 0 1 3 2 m mm      或 10 1 3 2 m mm      或 3 2 0 10 m m    ，解得 23 32m或 m  或 1m  ，所以不等式的解集为 . 6.已知幂函数 的图象过点 ，则函数 在区间 上的最小值是( ) A. B. 0 C. D. 【答案】B 【解析】由题设 ，故 在 上单调递增，则当 时取最小值 ，应选答案 B. 7．已知函数 f(x)＝x2－2x＋4 在区间[0，m](m>0)上的最大值为 4，最小值为 3，则实数 m 的取值范围是( ) A．[1,2] B．(0,1] C．(0,2] D．[1，＋∞) 【答案】A 【解析】作出函数的图象如图所示，从图中可以看出当 1≤m≤2 时，函数 f(x)＝x2－2x＋4 在区间[0，m](m>0) 上的最大值为 4，最小值为 3。 8.【2017 山东，理 10】已知当  0 ,1x  时，函数   21y m x的图象与 y x m的图象有且只有一个 交点，则正实数 m 的取值范围是 （A）   0,123,  （B）    0 ,1 3 ,  （C）  0,223,  （D）   0 , 2 3 ,   【答案】B 【解析】试题分析：当 01m时， 1 1m  ， 2( 1)y m x 单调递减，且 22(1)[(1),1]ymxm ， y x m单调递增，且 [,1]yxmmm ，此时有且仅有一个交点；当 1m  时， 101m ， 在 1[ ,1 ]m 上单调递增，所以要有且仅有一个交点，需 2(1)13mmm 选 B. 9.已知函数    2 2,2, 2,2, xx fx xx    函数    2gxbfx ，其中 bR ，若函数    yfxgx 恰有 4 个零点，则 b 的取值范围是( ) （A） 7 ,4  （B） 7, 4  （C） 70, 4   （D） 7 ,24   【答案】D 【解析】由    2 2,2, 2,2, xx fx xx    得 2 2 2 , 0 (2 ) ,0 xx fx xx     ， 所以 2 2 2 , 0 ( ) (2 ) 4 2 , 0 2 2 2 ( 2) , 2 x x x y f x f x x x x x x x                    ， 即 2 2 2, 0 ( ) (2 ) 2, 0 2 5 8, 2 x x x y f x f x x x x x               ， ( ) ( ) ( ) (2 )y f x g x f x f x b      ,所以 恰有 4 个零点等价于方程 ( ) (2 ) 0f x f x b    有 4 个不同的解，即函数 yb 与函数 ()(2)yfxfx 的图象的 4 个公共点，由图象可知 7 24 b. 8 6 4 2 2 4 6 8 15 10 5 5 10 15 10.已知函数 是定义在实数集 上的以 2 为周期的偶函数，当 时， .若直线 与函数 的图像在 内恰有两个不同的公共点，则实数 的值是( ) A． 或 ； B．0；C．0 或 ； D．0 或 . 【答案】D 【解析】根据已知可得函数 2( )(2 ) ,[21,21),fxxkxkkkZ ，在直角坐标系中作出它的图象， 如图，再作直线 yxa，可见当直线 yxa与抛物线 2yx 相切时，或者直线 yxa过原点时， 符合题意，此时 1 4a  或 0a  . 11．【2019 年高考天津文数】已知函数 2 , 0 1, () 1 , 1. xx fx xx     若关于 x 的方程 1( ) ( )4f x x a a   R 恰有两个互异的实数解，则 a 的取值范围为 A． 59,44   B． 59,44    C． 59, {1}44    D． 59, {1}44   【答案】D 【解析】作出函数 2,01, () 1 ,1 xx fx xx     的图象，以及直线 1 4yx ，如图， 关于 x 的方程 1()() 4fxxaa  R 恰有两个互异的实数解，即为 ()yfx 和 1 ()4yxaa  R 的图 象有两个交点，平移直线 ，考虑直线经过点 ( 1 , 2 ) 和 ( 1 , 1 ) 时，有两个交点，可得 9 4a  或 5 4a  ， 考虑直线 与 1y x 在 1x  时相切， 21 14ax x，由 2 10a  ，解得 1a  （ 1 舍去），所以 a 的取值范围是  59,149   .故选 D. 【名师点睛】根据方程实数根的个数确定参数的取值范围，常把其转化为曲线的交点个数问题，特别是其 中一个函数的图象为直线时常用此法. 12．已知不等式 对于 恒成立，则 的取值范围是 A． B． C． D． 【答案】C 【解析】不等式 对于 恒成立，等价于 对于 恒 成立，令 ，则 ， 在 上恒成立， ， 时， ， ，故 的取值范围是 .故选 C． 13．已知 ()fx为幂函数，且满足 (8) 2(2 ) f f  ，若 ( 1) 1fm，则实数 m 的取值范围是_________. 【答案】  1, 2 【解析】设 () af x x= ， 32(8)8 2222(2)2 a aaa a f f  ，解得 1 2a  ， 1 2()f x x，且函数 在 [0 , ) 上单调递增， 1 2(1)(1)1fmm ， 11 10 m m    … ，解得 [1,2 )m  。 14．若方程 x2＋(k－2)x＋2k－1＝0 的两根中，一根在 0 和 1 之间，另一根在 1 和 2 之间，则实数 k 的取值 范围是____________． 【答案】 12( , )23 【解析】设 f(x)＝x2＋(k－2)x＋2k－1，由题意知       00 10 20 f f f       即 2 1 0 3 2 0 4 1 0 k k k      解得 1 2

查看更多